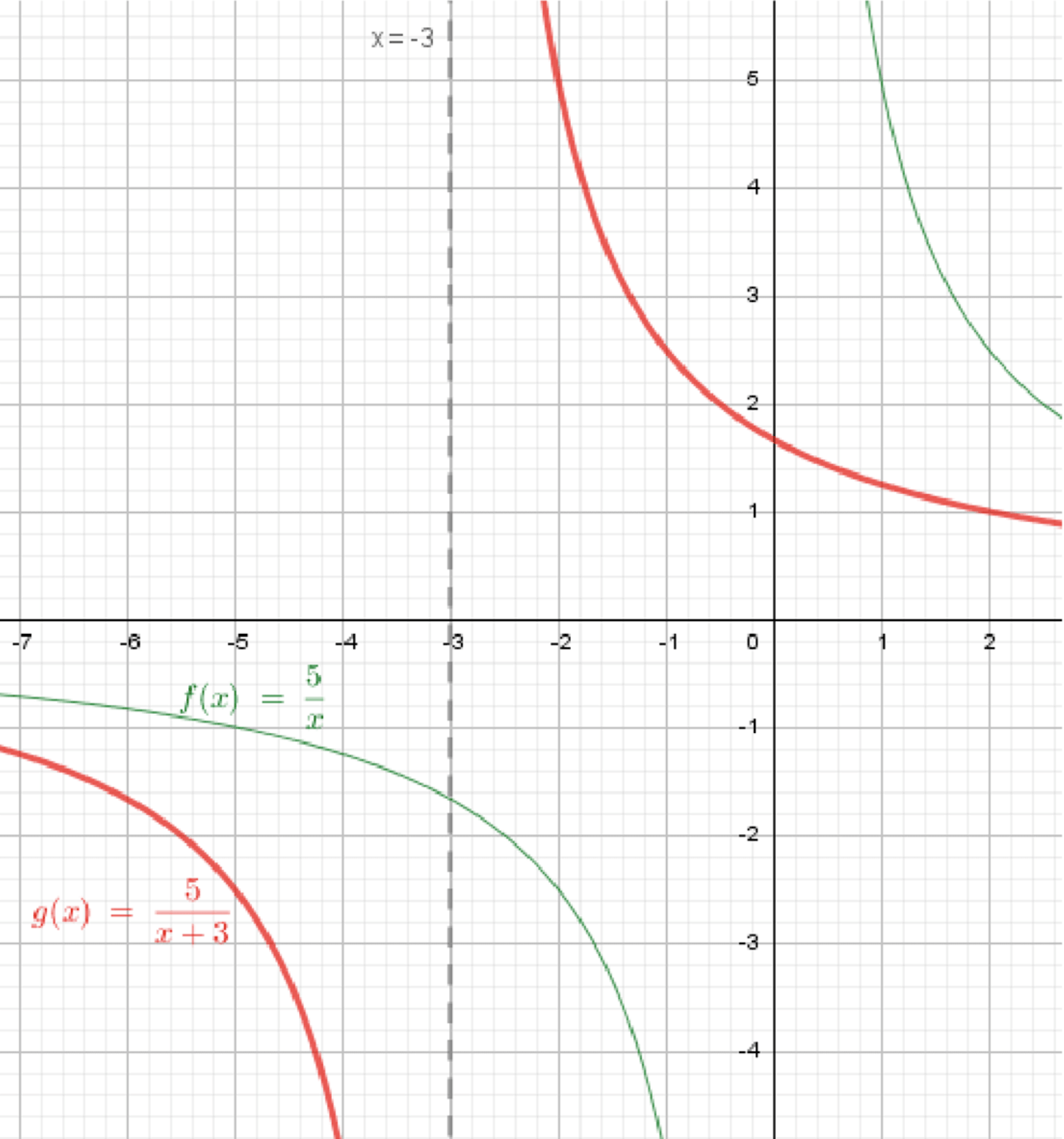ГДЗ 10-11 Класс Номер 1.11 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график заданной функции, найдите область определения и область значений функции:

а) $y=\frac{1}{x}+3$

б) $y=\frac{5}{x+3}$

в) $y=\frac{-2}{x}-1$

г) $y=\frac{4}{1-x}$

Построить график заданной функции, найти область определения и область значений функции:

а) $y=\frac{1}{x}+3$

• Построим график функции $y=\frac{1}{x}$;
• Перенесем его на 3 единицы вверх:

Ответ:

$$D(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty });$$$$E(y)=(-\mathrm{\infty };3)\cup (3;+\mathrm{\infty })\mathrm{.}$$

б) $y=\frac{5}{x+3}$

• Построим график функции $y=\frac{1}{x}$;
• Растянем его в 5 раз от оси абсцисс;
• Перенесем его на 3 единицы влево:

Ответ:

$$D(y)=(-\mathrm{\infty };-3)\cup (-3;+\mathrm{\infty });$$$$E(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })\mathrm{.}$$

в) $y=\frac{-2}{x}-1$

• Построим график функции $y=-\frac{1}{x}$;
• Растянем его в 2 раза от оси абсцисс;
• Перенесем его на 1 единицу вниз:

Ответ:

$$D(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty });$$$$E(y)=(-\mathrm{\infty };-1)\cup (-1;+\mathrm{\infty })\mathrm{.}$$

г) $y=\frac{4}{1-x}$

• Построим график функции $y=-\frac{1}{x}$;
• Растянем его в 4 раза от оси абсцисс;
• Перенесем его на 1 единицу вправо:

Ответ:

$$D(y)=(-\mathrm{\infty };1)\cup (1;+\mathrm{\infty });$$$$E(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })\mathrm{.}$$

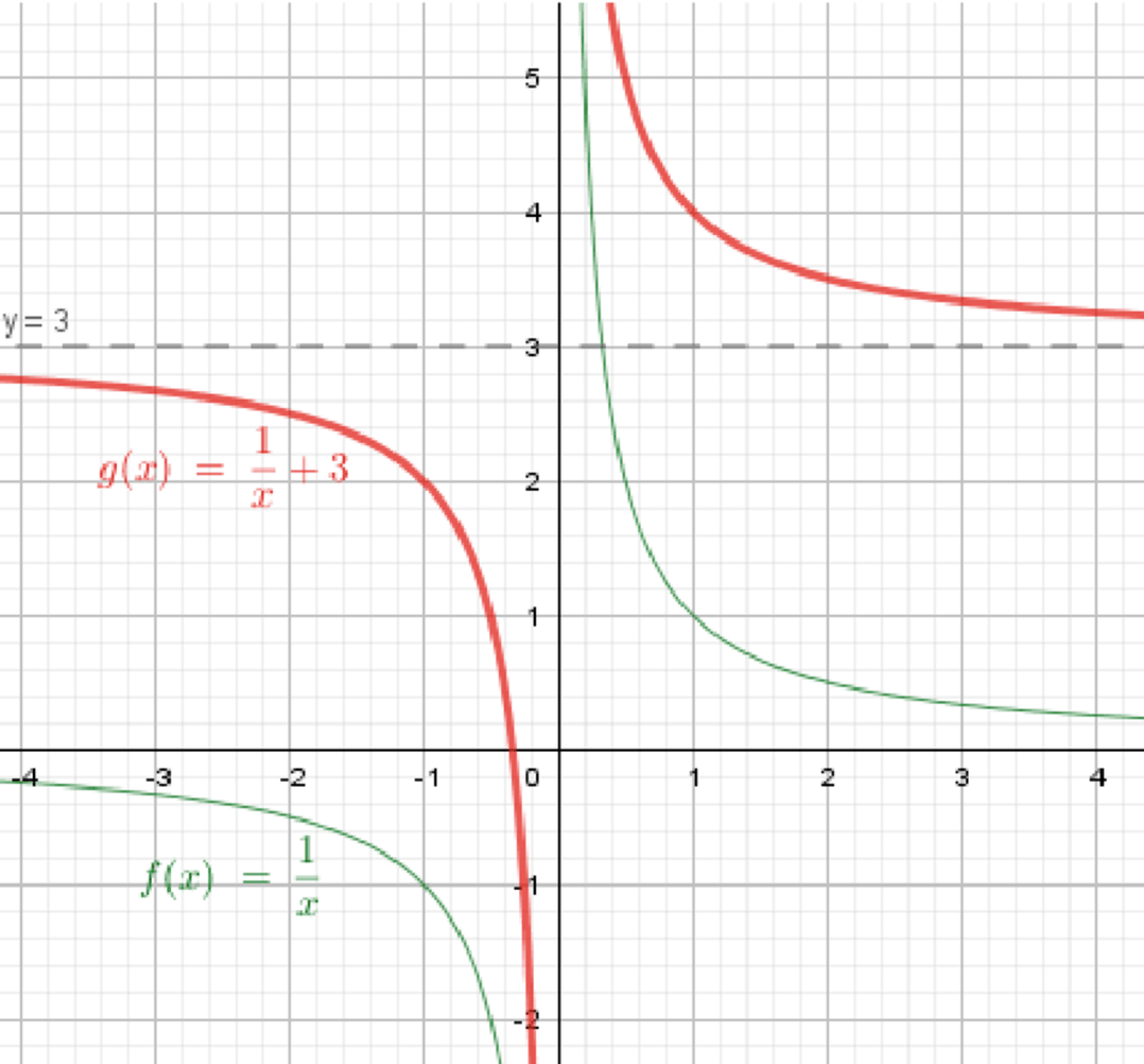
а) $y=\frac{1}{x}+3$

Шаг 1: Область определения $D(y)$

Функция $y=\frac{1}{x}+3$ имеет дробь, где переменная $x$ находится в знаменателе. Функция не определена, когда знаменатель равен нулю. Таким образом, для функции $y=\frac{1}{x}$ область определения будет:

$$x\mathrm{\ne }0$$

То есть $x$ может принимать любые значения, кроме нуля. Область определения:

$$D(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$$

Шаг 2: Область значений $E(y)$

Функция $y=\frac{1}{x}$ имеет гиперболическую форму, и график будет асимптотичен оси $x$ при $y=0$ и оси $y$ при $x\to \mathrm{\infty }$. После сдвига функции на 3 единицы вверх, область значений функции сдвигается на 3 единицы вверх. Таким образом, минимальное значение функции будет приближаться к 3, но никогда не достигнет её, так как гиперболический график функции не пересекает линию $y=3$. Следовательно:

$$E(y)=(-\mathrm{\infty };3)\cup (3;+\mathrm{\infty })$$

Шаг 3: Построение графика

График функции $y=\frac{1}{x}$ имеет гиперболическую форму, и после переноса на 3 единицы вверх, график будет располагаться выше оси $x$. При $x\to 0^{+}$ или $x\to 0^{-}$, функция стремится к бесконечности (положительной или отрицательной), а при $x\to \mathrm{\infty }$ и $x\to -\mathrm{\infty }$, функция стремится к 3.

График функции:

Ответ:

$$D(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty }),E(y)=(-\mathrm{\infty };3)\cup (3;+\mathrm{\infty })$$

б) $y=\frac{5}{x+3}$

Шаг 1: Область определения $D(y)$

Для функции $y=\frac{5}{x+3}$ знаменатель $x+3$ не должен быть равен нулю, то есть:

$$x+3\mathrm{\ne }0$$

Решая это, получаем:

$$x\mathrm{\ne }-3$$

Следовательно, область определения функции:

$$D(y)=(-\mathrm{\infty };-3)\cup (-3;+\mathrm{\infty })$$

Шаг 2: Область значений $E(y)$

График функции $y=\frac{1}{x}$ будет гиперболическим, но для $y=\frac{5}{x+3}$, график будет сдвигаться влево на 3 единицы. Значения $y$ будут стремиться к 0, но никогда её не достигнут. Таким образом, функция может принимать все значения, кроме нуля. Область значений:

$$E(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$$

Шаг 3: Построение графика

График функции $y=\frac{5}{x+3}$ будет гиперболическим и сдвинутым на 3 единицы влево. Он будет асимптотичен к прямым $x=-3$ (вертикальная асимптота) и $y=0$ (горизонтальная асимптота).

График функции:

Ответ:

$$D(y)=(-\mathrm{\infty };-3)\cup (-3;+\mathrm{\infty }),E(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$$

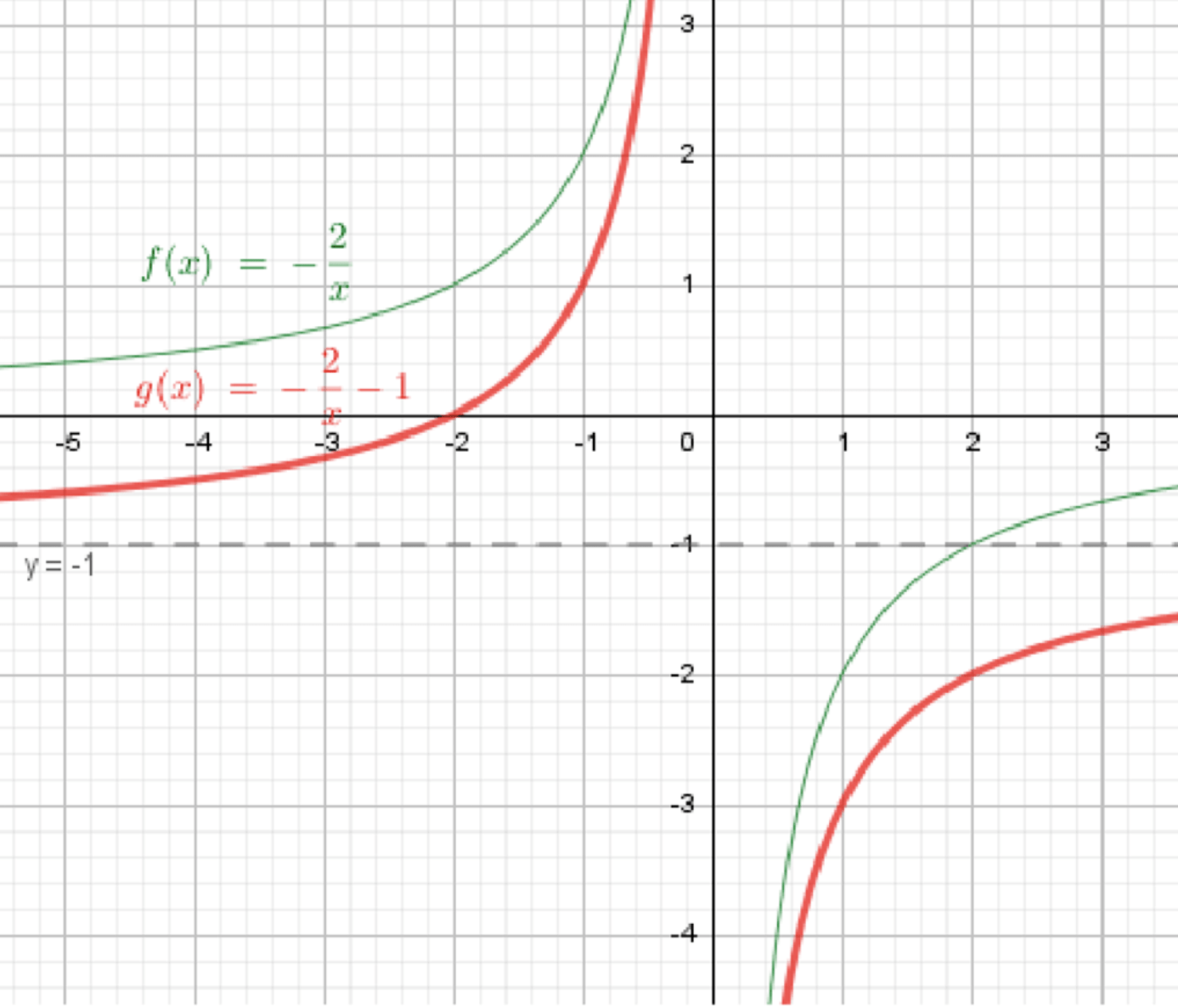
в) $y=\frac{-2}{x}-1$

Шаг 1: Область определения $D(y)$

Для функции $y=\frac{-2}{x}-1$ знаменатель не должен быть равен нулю, то есть:

$$x\mathrm{\ne }0$$

Следовательно, область определения функции:

$$D(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$$

Шаг 2: Область значений $E(y)$

Функция $y=\frac{-2}{x}$ будет гиперболой, которая сдвигается на 1 единицу вниз. Аналогично предыдущим функциям, она будет стремиться к нулю, но никогда его не достигнет, только теперь ось $y=-1$ будет являться горизонтальной асимптотой. Значения функции могут быть любыми, кроме -1. Область значений:

$$E(y)=(-\mathrm{\infty };-1)\cup (-1;+\mathrm{\infty })$$

Шаг 3: Построение графика

График функции $y=\frac{-2}{x}$ будет гиперболическим, открытым влево и вправо, а затем весь график будет сдвинут вниз на 1 единицу.

График функции:

Ответ:

$$D(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty }),E(y)=(-\mathrm{\infty };-1)\cup (-1;+\mathrm{\infty })$$

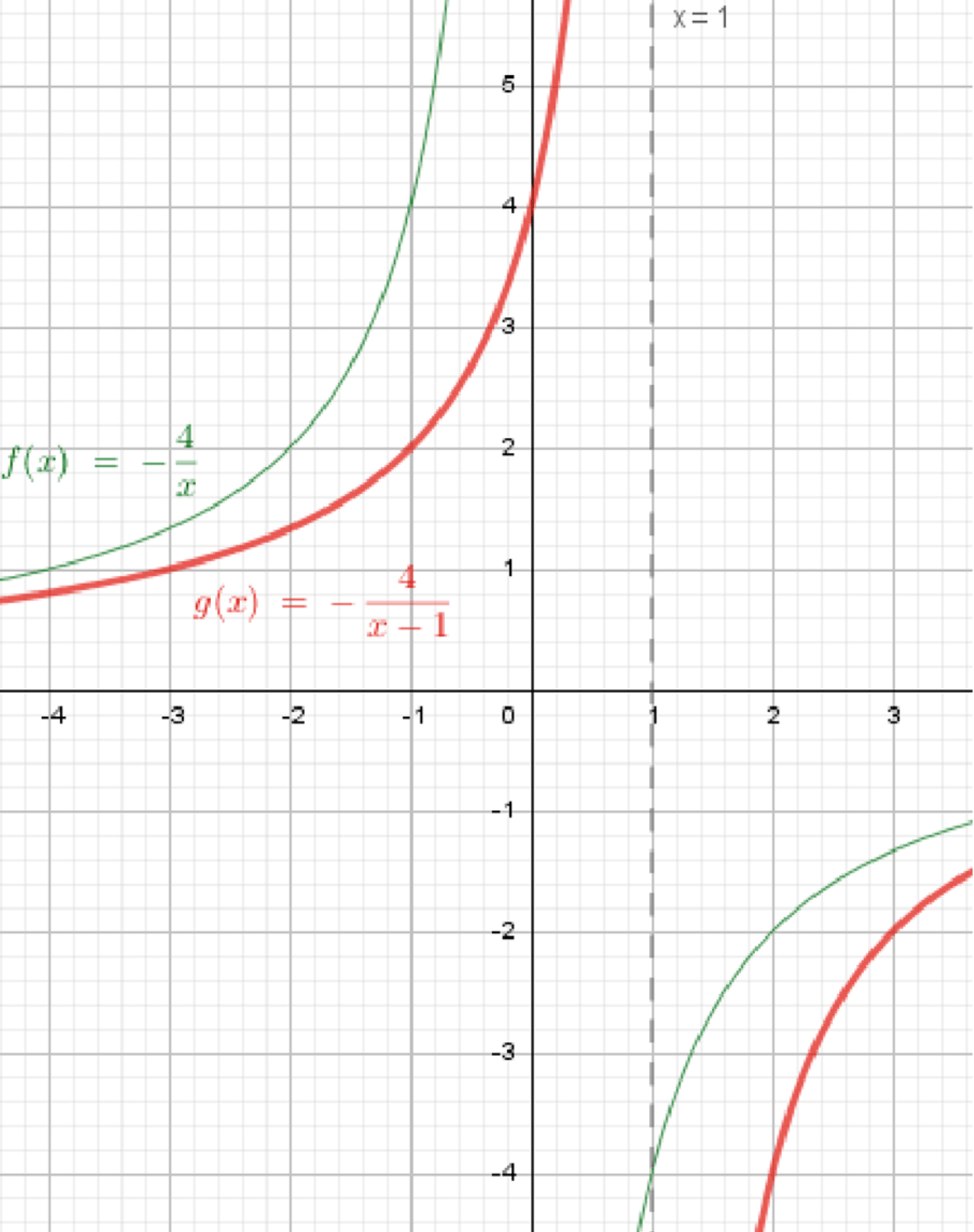
г) $y=\frac{4}{1-x}$

Шаг 1: Область определения $D(y)$

Для функции $y=\frac{4}{1-x}$ знаменатель не должен быть равен нулю, то есть:

$$1-x\mathrm{\ne }0$$

Решая это, получаем:

$$x\mathrm{\ne }1$$

Следовательно, область определения функции:

$$D(y)=(-\mathrm{\infty };1)\cup (1;+\mathrm{\infty })$$

Шаг 2: Область значений $E(y)$

График функции $y=\frac{1}{x}$ будет гиперболой, но для $y=\frac{4}{1-x}$ график будет сдвигаться на 1 единицу вправо. Аналогично предыдущим функциям, функция будет стремиться к нулю, но никогда его не достигнет. Таким образом, область значений:

$$E(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$$

Шаг 3: Построение графика

График функции $y=\frac{4}{1-x}$ будет гиперболическим и сдвинутым на 1 единицу вправо. Он будет асимптотичен к прямым $x=1$ и $y=0$.

График функции:

Ответ:

$$D(y)=(-\mathrm{\infty };1)\cup (1;+\mathrm{\infty }),E(y)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$$