ГДЗ 10-11 Класс Номер 1.12 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график заданной функции, найдите область определения и область значений функции:

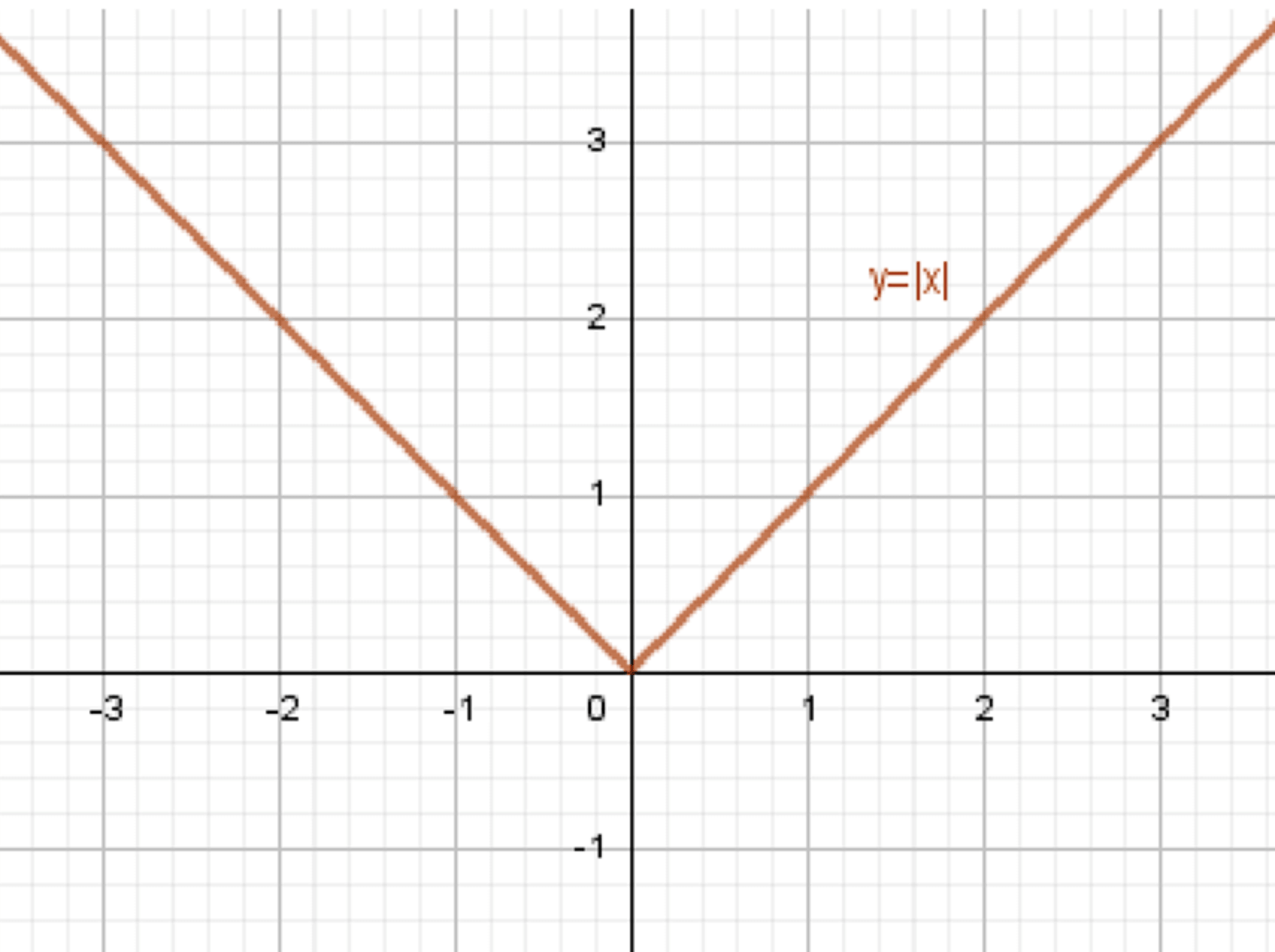
а) у = |x|;

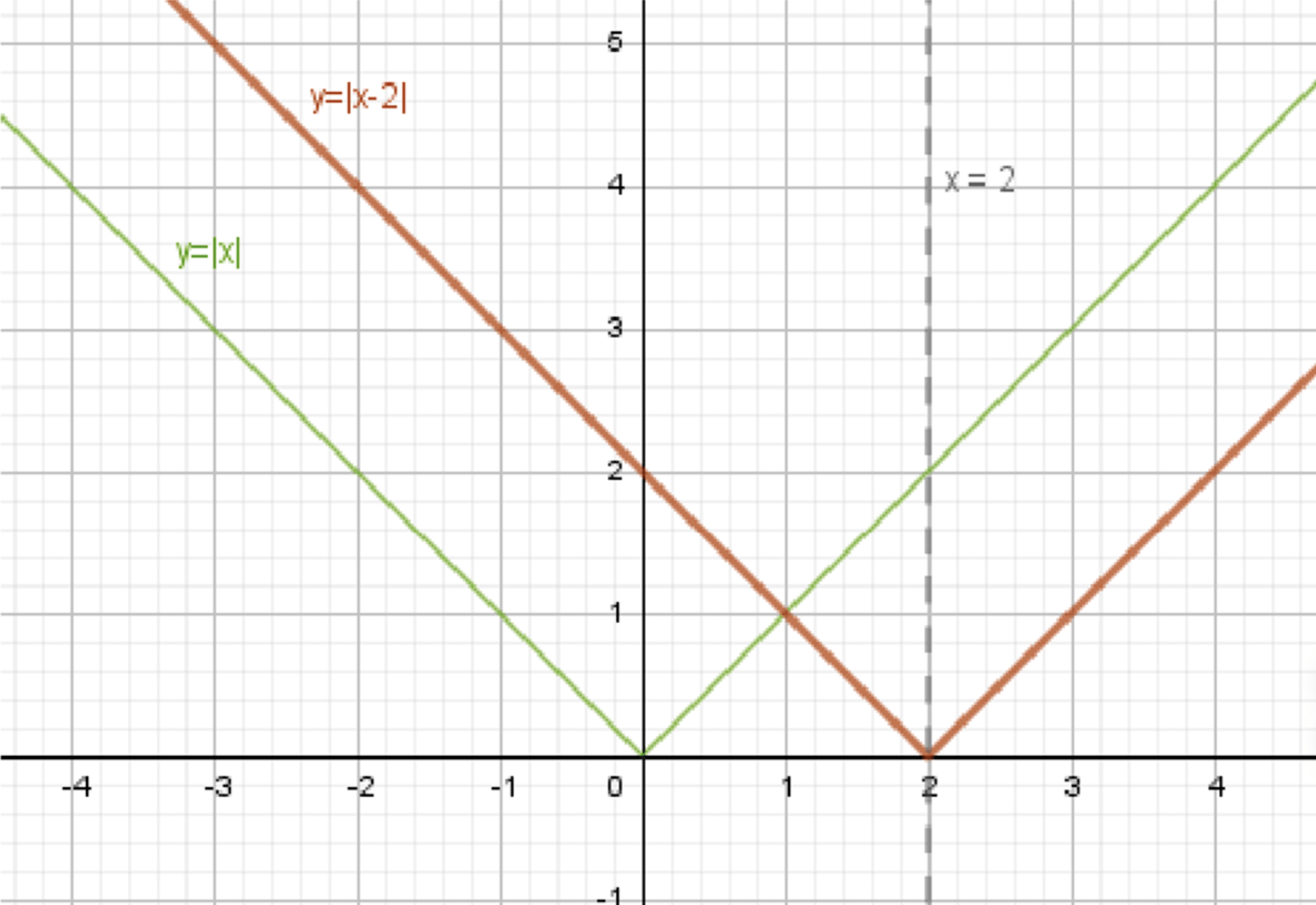
б) у = |х — 2|;

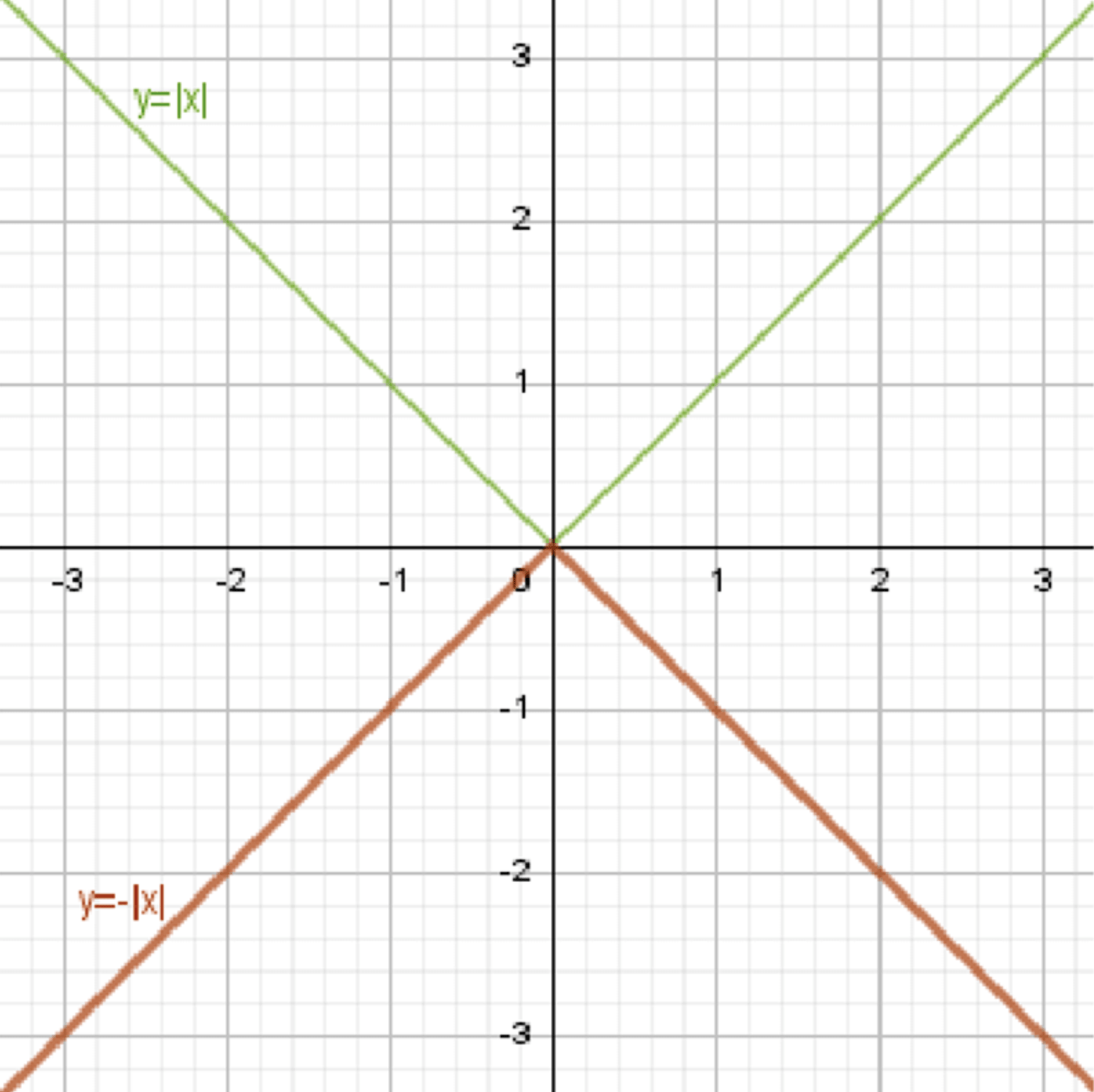
в) у = -|х|;

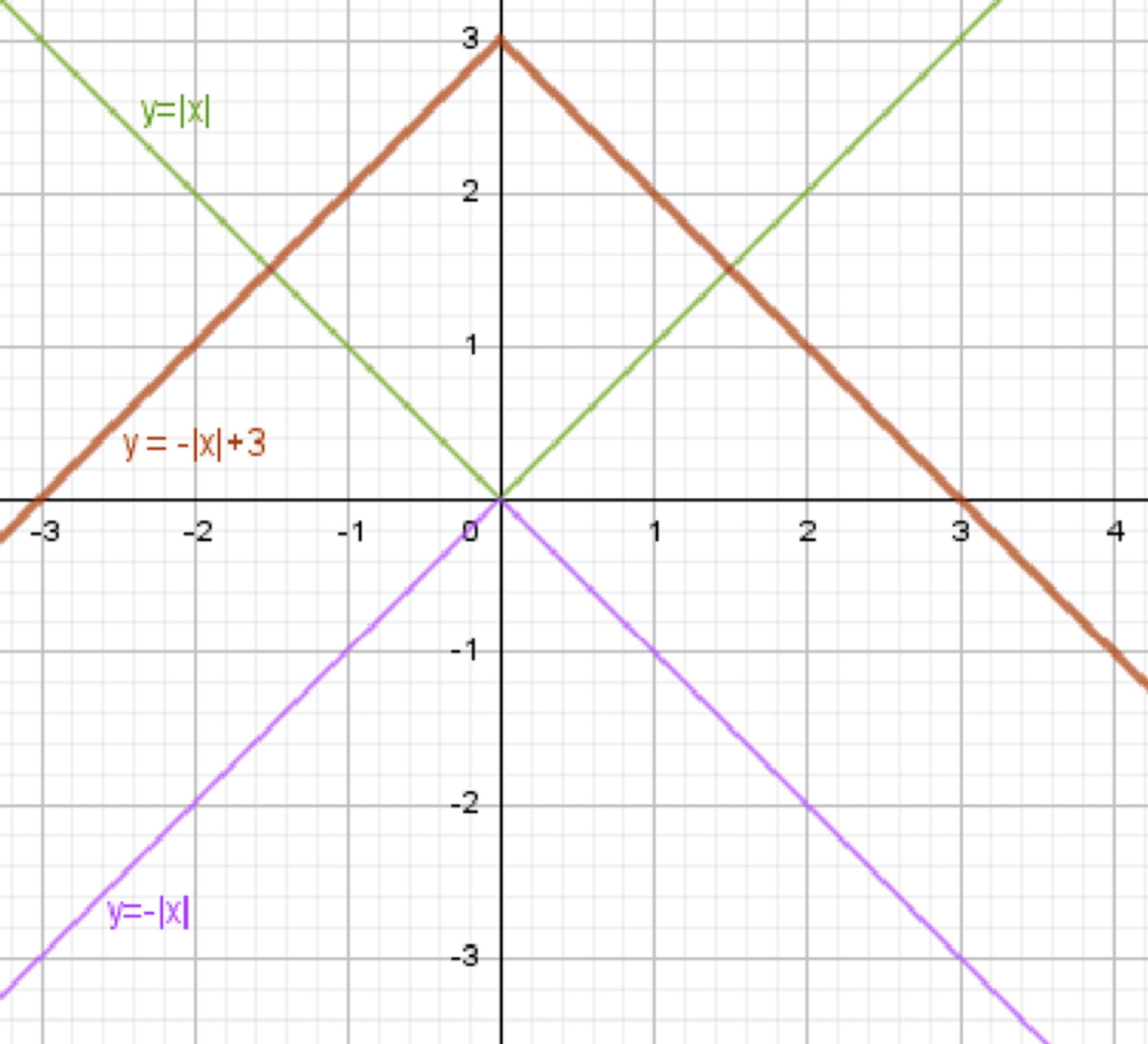
г) у = 3 — |x|.

Построить график заданной функции, найти область определения и область значений функции:

а) $y=\mathrm{\mid }x\mathrm{\mid }$;

Построим график функции $y=\mathrm{\mid }x\mathrm{\mid }$:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty });E(y)=[0;+\mathrm{\infty })$.

б) $y=\mathrm{\mid }x-2\mathrm{\mid }$;

Построим график функции $y=\mathrm{\mid }x\mathrm{\mid }$;

Перенесем его на 2 единицы вправо:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty });E(y)=[0;+\mathrm{\infty })$.

в) $y=-\mathrm{\mid }x\mathrm{\mid }$;

Построим график функции $y=\mathrm{\mid }x\mathrm{\mid }$;

Отразим его относительно оси абсцисс:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty });E(y)=(-\mathrm{\infty };0]$.

г) $y=3-\mathrm{\mid }x\mathrm{\mid }$;

Построим график функции $y=\mathrm{\mid }x\mathrm{\mid }$;

Отразим его относительно оси абсцисс;

Перенесем его на 3 единицы вверх:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty });E(y)=(-\mathrm{\infty };3]$.

а) $y=\mathrm{\mid }x\mathrm{\mid }$

Шаг 1: Область определения $D(y)$

Функция $y=\mathrm{\mid }x\mathrm{\mid }$ является абсолютной величиной. Абсолютная величина от любого числа существует, то есть для всех значений $x$ функция определена. Следовательно, область определения функции:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Шаг 2: Область значений $E(y)$

Функция $y=\mathrm{\mid }x\mathrm{\mid }$ всегда принимает неотрицательные значения, так как абсолютная величина любого числа $x$ всегда больше либо равна нулю. Минимальное значение функции $y=\mathrm{\mid }x\mathrm{\mid }$ достигается при $x=0$, и оно равно 0. С увеличением $\mathrm{\mid }x\mathrm{\mid }$ (абсолютной величины $x$), значение $y$ также увеличивается. Таким образом, область значений функции:

$$E(y)=[0;+\mathrm{\infty })$$

Шаг 3: Построение графика

График функции $y=\mathrm{\mid }x\mathrm{\mid }$ представляет собой «V»-образную кривую, которая имеет вершину в точке $(0,0)$. При $x>0$ график будет прямой с угловым коэффициентом 1, а при $x<0$ график будет прямой с угловым коэффициентом -1.

График функции:

Ответ:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty }),E(y)=[0;+\mathrm{\infty })$$

б) $y=\mathrm{\mid }x-2\mathrm{\mid }$

Шаг 1: Область определения $D(y)$

Функция $y=\mathrm{\mid }x-2\mathrm{\mid }$ также является функцией абсолютной величины, и для любых значений $x$ она будет определена. Следовательно, область определения этой функции:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Шаг 2: Область значений $E(y)$

Как и в случае с функцией $y=\mathrm{\mid }x\mathrm{\mid }$, функция $y=\mathrm{\mid }x-2\mathrm{\mid }$ всегда принимает неотрицательные значения, так как это абсолютная величина. Минимальное значение функции достигается в точке $x=2$, где $y=\mathrm{\mid }2-2\mathrm{\mid }=0$. При $x$ удаляющемся от 2, значение функции увеличивается. Таким образом, область значений:

$$E(y)=[0;+\mathrm{\infty })$$

Шаг 3: Построение графика

График функции $y=\mathrm{\mid }x-2\mathrm{\mid }$ будет аналогичен графику функции $y=\mathrm{\mid }x\mathrm{\mid }$, но сдвинут на 2 единицы вправо. Вершина графика будет в точке $(2,0)$.

График функции:

Ответ:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty }),E(y)=[0;+\mathrm{\infty })$$

в) $y=-\mathrm{\mid }x\mathrm{\mid }$

Шаг 1: Область определения $D(y)$

Функция $y=-\mathrm{\mid }x\mathrm{\mid }$ также является функцией абсолютной величины, но с отрицательным знаком перед ней. Для всех значений $x$ функция будет определена. Следовательно, область определения:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Шаг 2: Область значений $E(y)$

Функция $y=-\mathrm{\mid }x\mathrm{\mid }$ всегда будет принимать отрицательные значения или ноль, так как абсолютная величина всегда неотрицательна, а знак минус перед ней делает все значения отрицательными. Минимальное значение $y$ будет при $x=0$, где $y=0$. Для всех других значений $x$, значение функции будет отрицательным. Таким образом, область значений:

$$E(y)=(-\mathrm{\infty };0]$$

Шаг 3: Построение графика

График функции $y=-\mathrm{\mid }x\mathrm{\mid }$ будет зеркальным отражением графика функции $y=\mathrm{\mid }x\mathrm{\mid }$ относительно оси $x$, так как перед абсолютной величиной стоит отрицательный знак. Вершина графика будет в точке $(0,0)$, и график будет направлен вниз.

График функции:

Ответ:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty }),E(y)=(-\mathrm{\infty };0]$$

г) $y=3-\mathrm{\mid }x\mathrm{\mid }$

Шаг 1: Область определения $D(y)$

Функция $y=3-\mathrm{\mid }x\mathrm{\mid }$ также является функцией абсолютной величины, и она определена для всех значений $x$. Следовательно, область определения:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Шаг 2: Область значений $E(y)$

Функция $y=3-\mathrm{\mid }x\mathrm{\mid }$ имеет форму параболы, направленной вниз, так как перед абсолютной величиной стоит знак минус. Максимальное значение функции будет в вершине параболы, которая будет при $x=0$, где:

$$y=3-\mathrm{\mid }0\mathrm{\mid }=3$$

С увеличением $\mathrm{\mid }x\mathrm{\mid }$ (абсолютной величины $x$), значение $y$ будет уменьшаться, стремясь к минус бесконечности, но не достигая его. Таким образом, область значений:

$$E(y)=(-\mathrm{\infty };3]$$

Шаг 3: Построение графика

График функции $y=3-\mathrm{\mid }x\mathrm{\mid }$ будет представлять собой параболу, направленную вниз, с вершиной в точке $(0,3)$. Это будет симметричная фигура относительно оси $y$, и по мере увеличения $\mathrm{\mid }x\mathrm{\mid }$ функция будет стремиться к минус бесконечности.

График функции:

Ответ:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty }),E(y)=(-\mathrm{\infty };3]$$