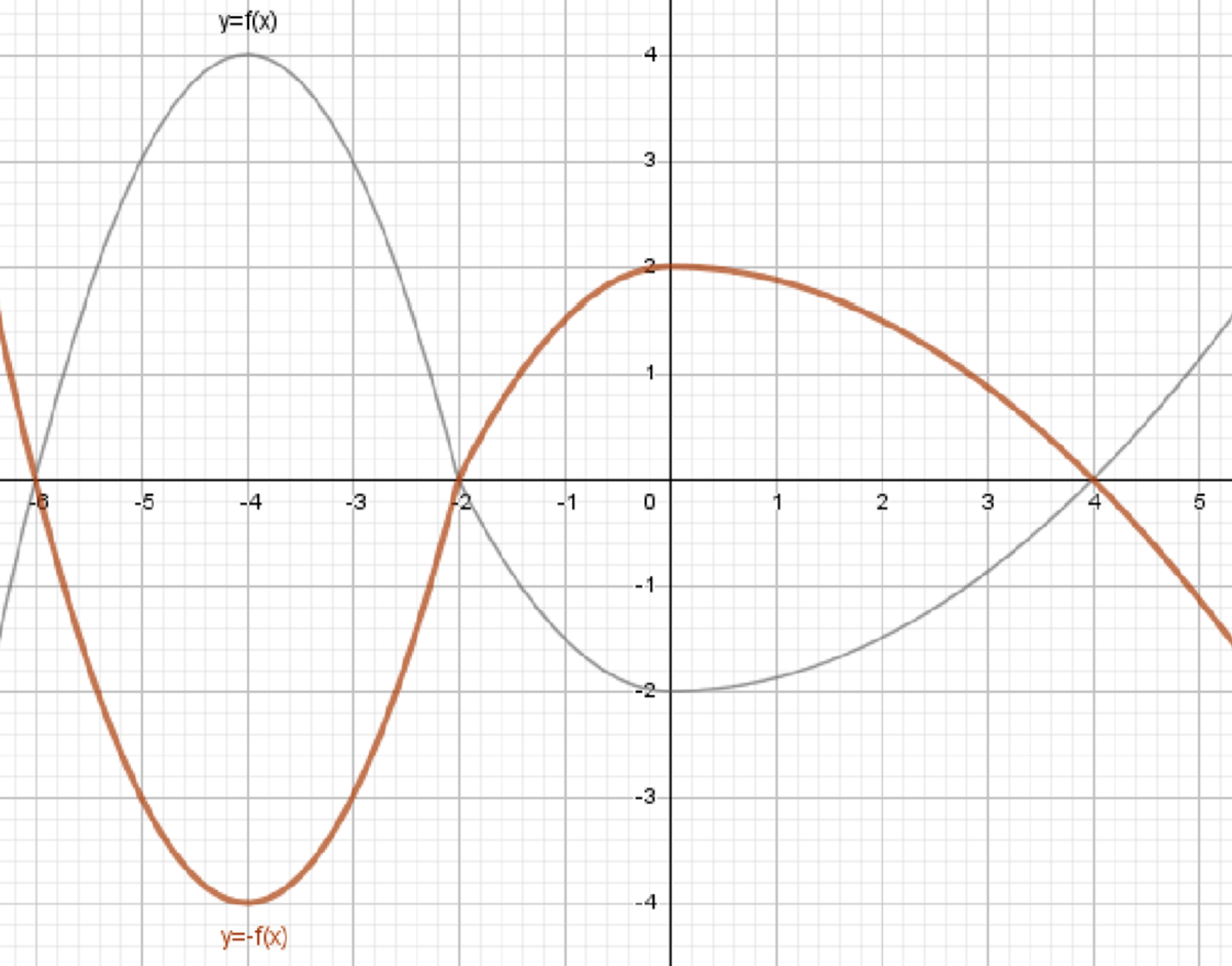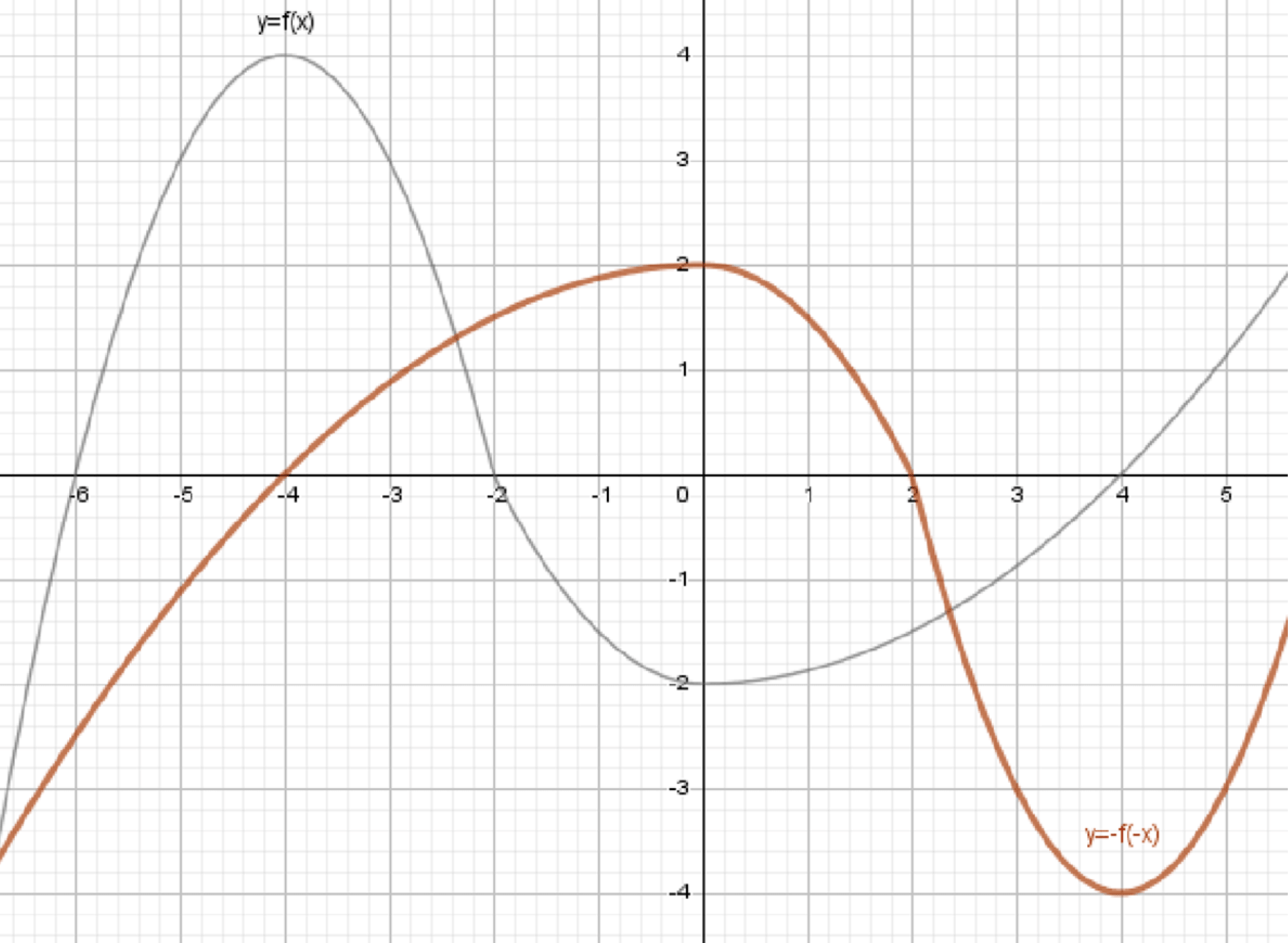ГДЗ 10-11 Класс Номер 1.14 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Используя график функции у = f(x), изображённый на рис. 1, постройте график функции:

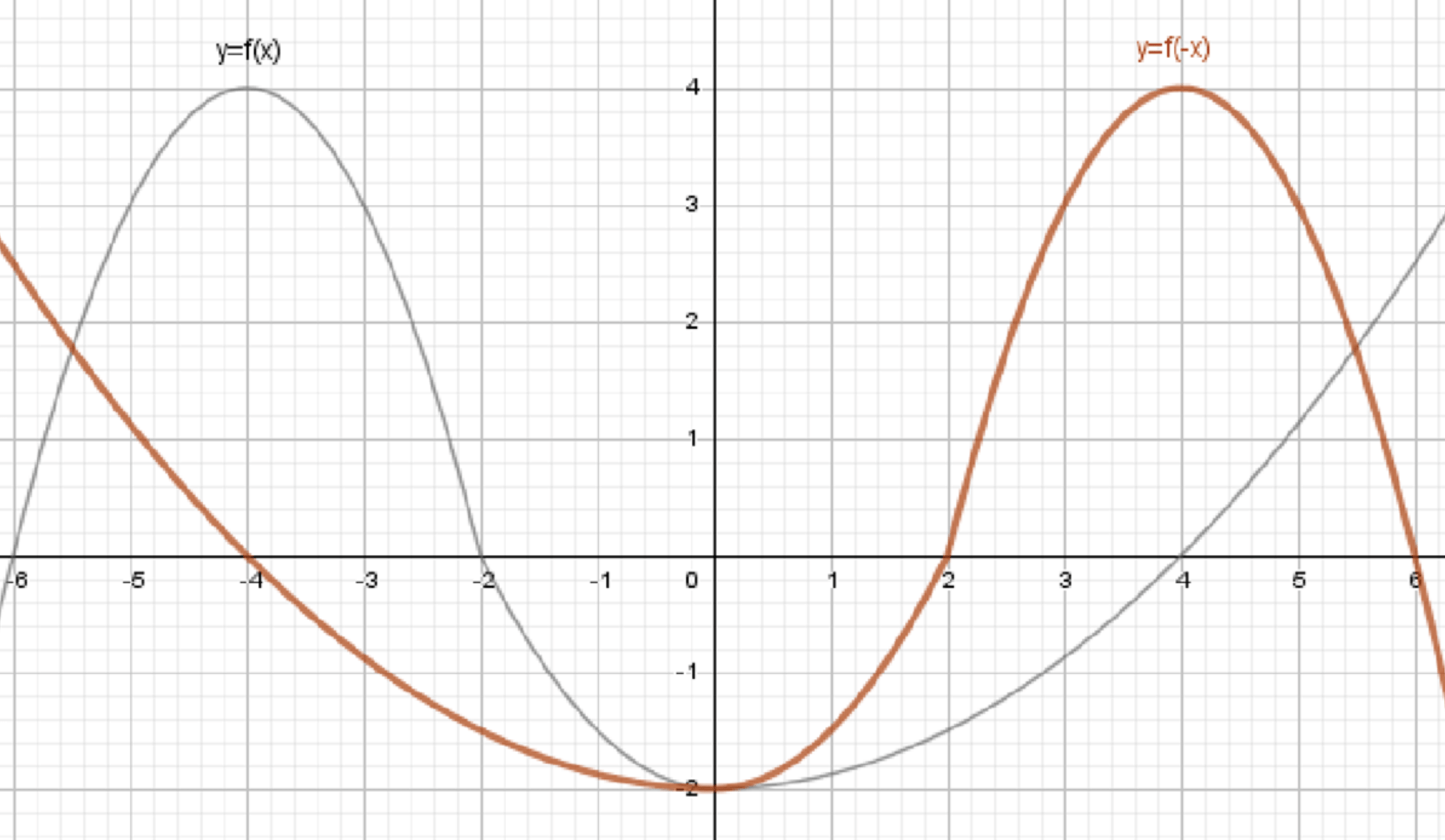
а) у = f(-x);

б) y = -f(x);

в) у = -f(-x);

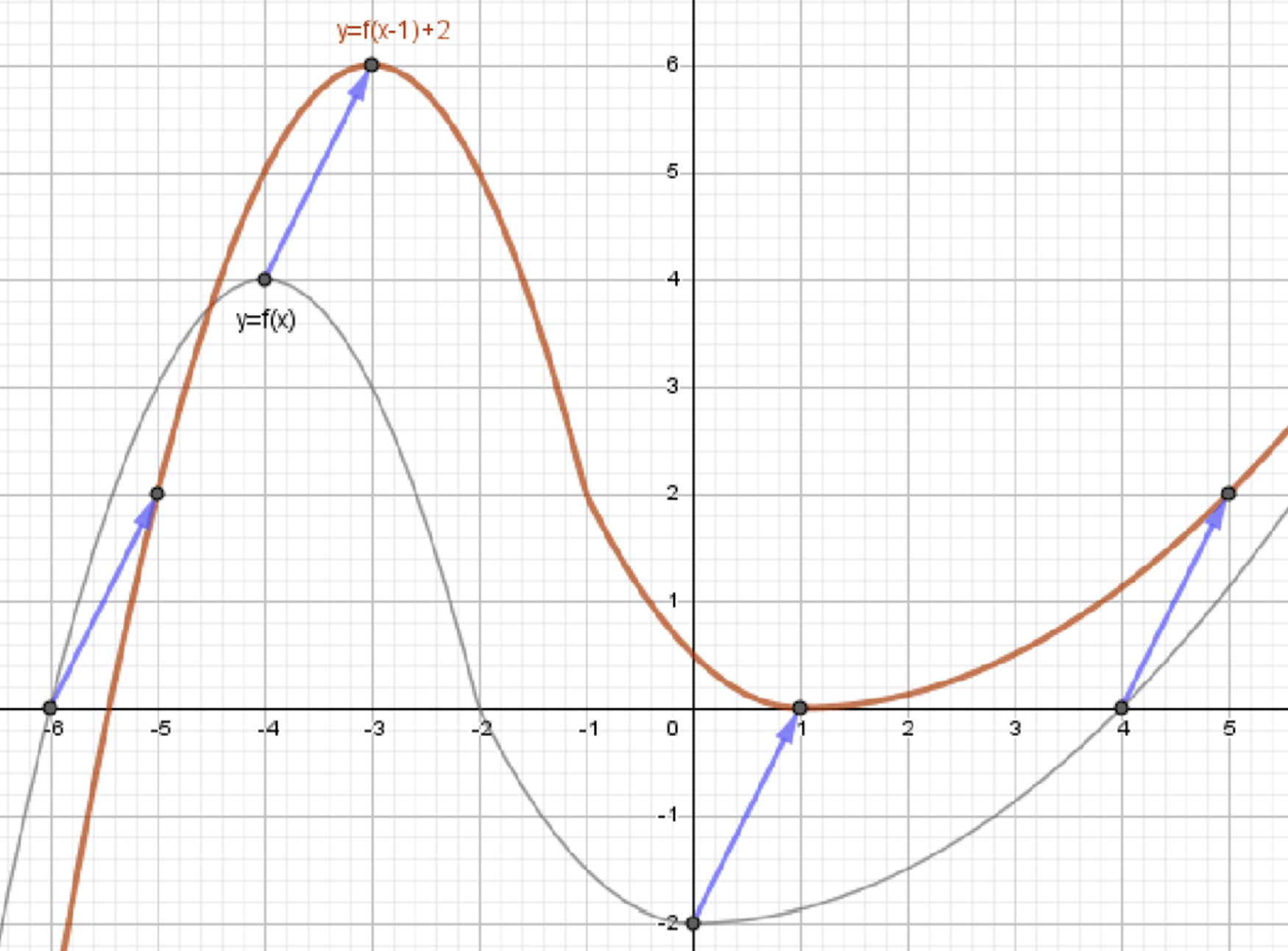
г) y = f(x-1) + 2.

Используя график функции $y=f(x)$, изображенный на рисунке 1, построить график функции:

а) $y=f(-x)$;
Отразим график относительно оси ординат:

б) $y=-f(x)$;
Отразим график относительно оси абсцисс:

в) $y=-f(-x)$;
Отразим график относительно осей координат:

г) $y=f(x-1)+2$;
Переносим график на 1 единицу вправо;
Переносим его на 2 единицы вверх:

Используя график функции $y=f(x)$, изображенный на рисунке 1, построим графики следующих функций.

а) $y=f(-x)$

Интерпретация:

Когда в аргументе функции появляется знак минус (как в $f(-x)$), график функции отражается относительно оси ординат (оси $y$). Это означает, что для каждого значения $x$ на графике функции $y=f(x)$, точка $(x,y)$ будет заменена на точку $(-x,y)$. Таким образом, функция будет симметрична относительно оси $y$.

Шаги:

1. Взять исходные точки графика функции $y=f(x)$.
2. Заменить все значения $x$ на их противоположные, т.е., для каждой точки $(x,y)$ будет новая точка $(-x,y)$.
3. Соединить все полученные точки.

Пример:

• Если на графике $y=f(x)$ есть точка $(3,5)$, то для функции $y=f(-x)$ будет точка $(-3,5)$.
• Если на графике $y=f(x)$ есть точка $(-2,4)$, то для функции $y=f(-x)$ будет точка $(2,4)$.

График:

б) $y=-f(x)$

Интерпретация:

Когда функция $y=f(x)$ меняется на $y=-f(x)$, это означает, что график функции отражается относительно оси абсцисс (оси $x$). Все точки графика функции $y=f(x)$ при этом будут изменяться на симметричные относительно оси $x$, то есть для каждой точки $(x,y)$ будет новая точка $(x,-y)$.

Шаги:

1. Взять исходные точки графика функции $y=f(x)$.
2. Для каждой точки $(x,y)$ на графике новой функции будет точка $(x,-y)$.
3. Соединить все полученные точки.

Пример:

• Если на графике $y=f(x)$ есть точка $(3,5)$, то для функции $y=-f(x)$ будет точка $(3,-5)$.
• Если на графике $y=f(x)$ есть точка $(-2,4)$, то для функции $y=-f(x)$ будет точка $(-2,-4)$.

График:

в) $y=-f(-x)$

Интерпретация:

Функция $y=-f(-x)$ представляет собой комбинацию двух операций:

1. Отражение графика функции $y=f(x)$ относительно оси ординат, то есть заменяем $x$ на $-x$, превращая график в $y=f(-x)$.
2. Отражение полученного графика относительно оси абсцисс, то есть изменяем знак всех значений $y$, превращая $y=f(-x)$ в $y=-f(-x)$.

Таким образом, сначала мы отражаем график относительно оси $y$, а затем — относительно оси $x$, что эквивалентно повороту графика на 180 градусов относительно начала координат.

Шаги:

1. Отразить исходный график функции $y=f(x)$ относительно оси ординат, получив $y=f(-x)$.
2. Отразить полученный график относительно оси абсцисс, получив $y=-f(-x)$.
3. Соединить все полученные точки.

Пример:

• Если на графике $y=f(x)$ есть точка $(3,5)$, то для функции $y=f(-x)$ будет точка $(-3,5)$, а для $y=-f(-x)$ будет точка $(-3,-5)$.
• Если на графике $y=f(x)$ есть точка $(-2,4)$, то для функции $y=f(-x)$ будет точка $(2,4)$, а для $y=-f(-x)$ будет точка $(2,-4)$.

График:

г) $y=f(x-1)+2$

Интерпретация:

Функция $y=f(x-1)+2$ представляет собой комбинацию двух операций:

1. Перемещение графика функции $y=f(x)$ на 1 единицу вправо. Это происходит из-за того, что $x$ заменяется на $x-1$. Все точки на графике сдвигаются вправо, и для каждой точки $(x,y)$ будет новая точка $(x+1,y)$.
2. Перемещение графика функции, полученной на предыдущем шаге, на 2 единицы вверх. Это происходит за счет добавления 2 к значению функции: $y=f(x-1)+2$.

Шаги:

1. Переместить график функции $y=f(x)$ на 1 единицу вправо. Для каждой точки $(x,y)$ новой функции будет точка $(x+1,y)$.
2. Переместить полученный график на 2 единицы вверх. Для каждой точки $(x,y)$ будет новая точка $(x,y+2)$.
3. Соединить все полученные точки.

Пример:

• Если на графике $y=f(x)$ есть точка $(3,5)$, то после сдвига на 1 вправо будет точка $(4,5)$, а после сдвига на 2 вверх будет точка $(4,7)$.
• Если на графике $y=f(x)$ есть точка $(-2,4)$, то после сдвига на 1 вправо будет точка $(-1,4)$, а после сдвига на 2 вверх будет точка $(-1,6)$.

График: