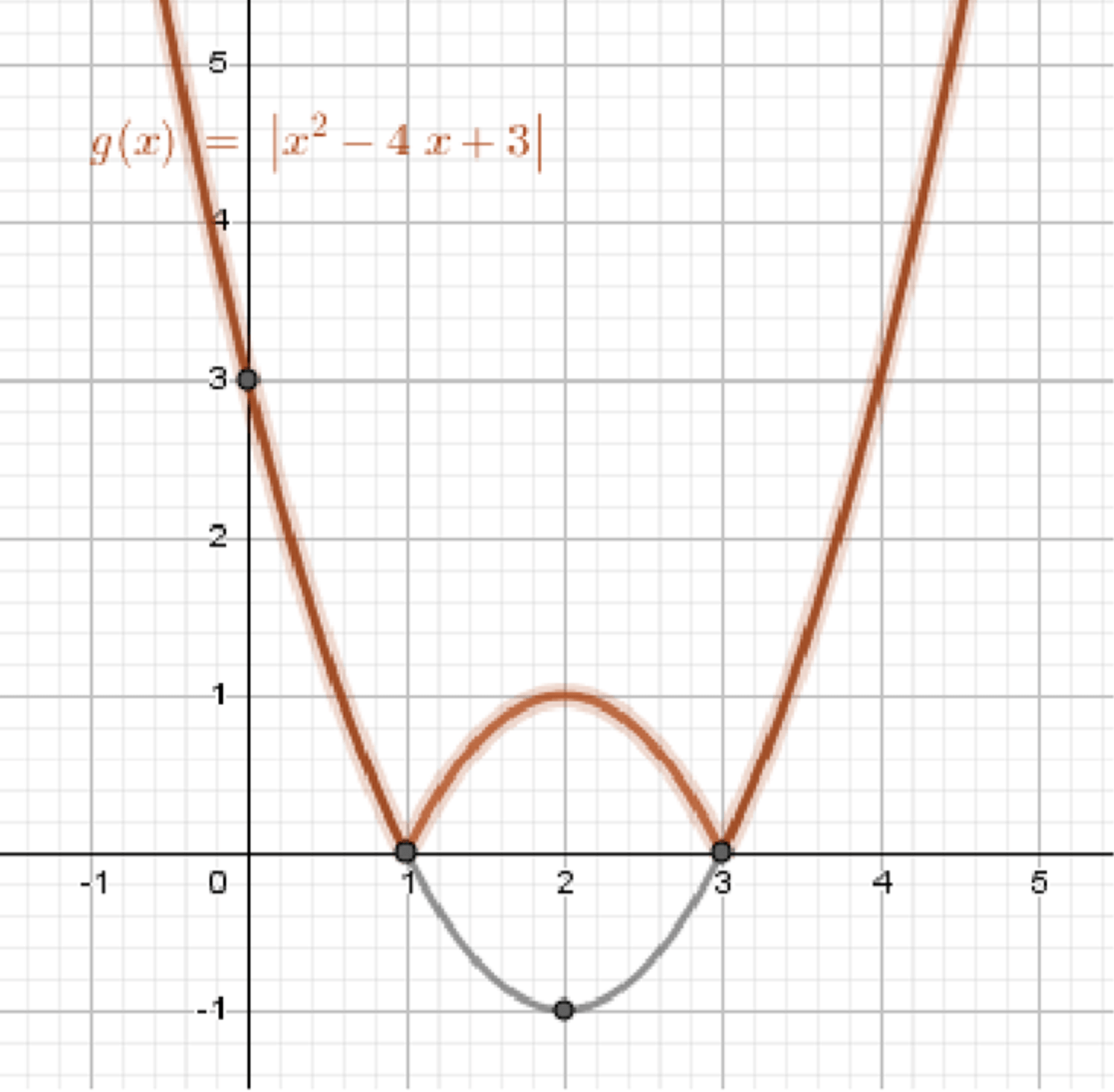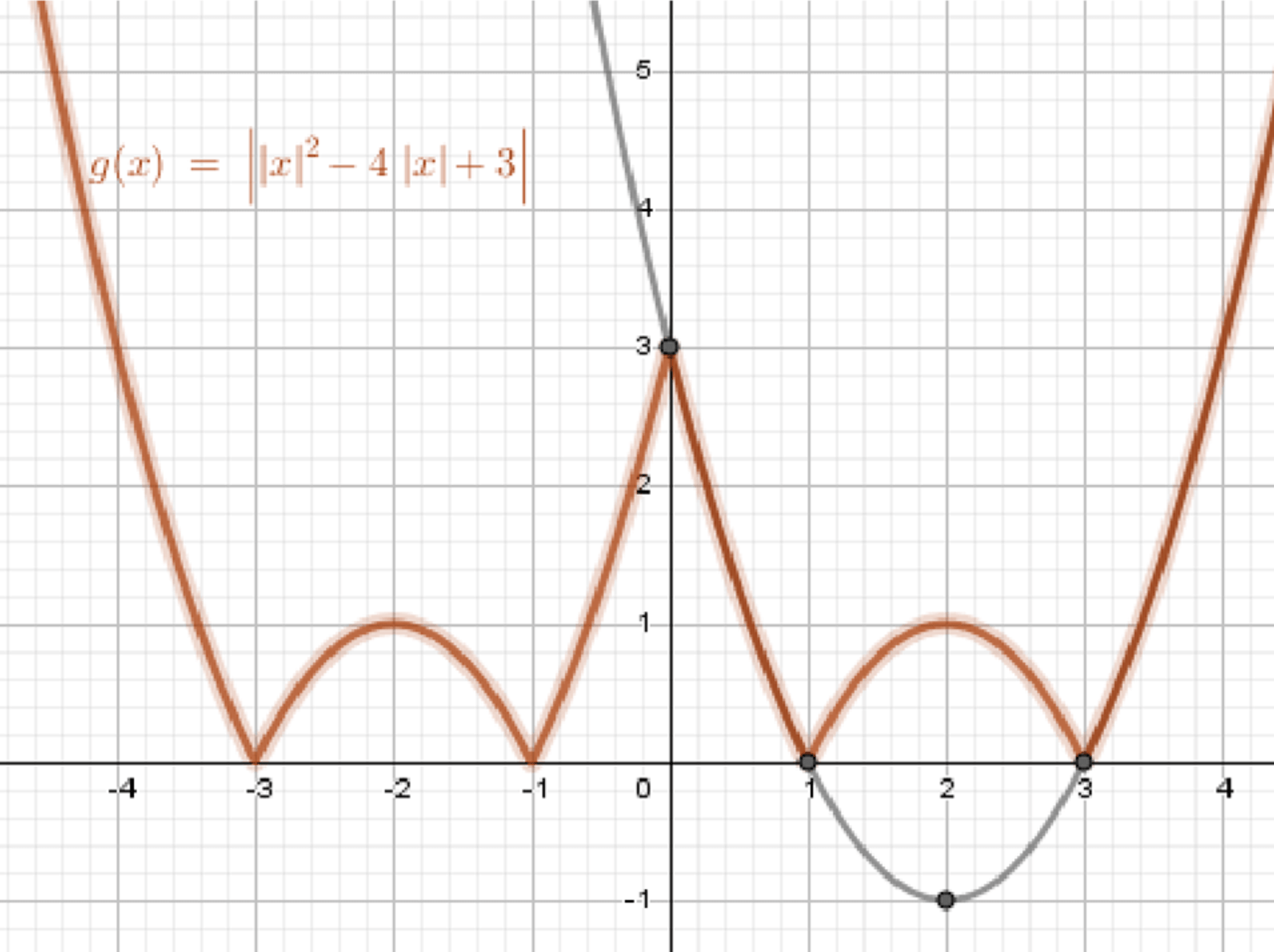ГДЗ 10-11 Класс Номер 1.15 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

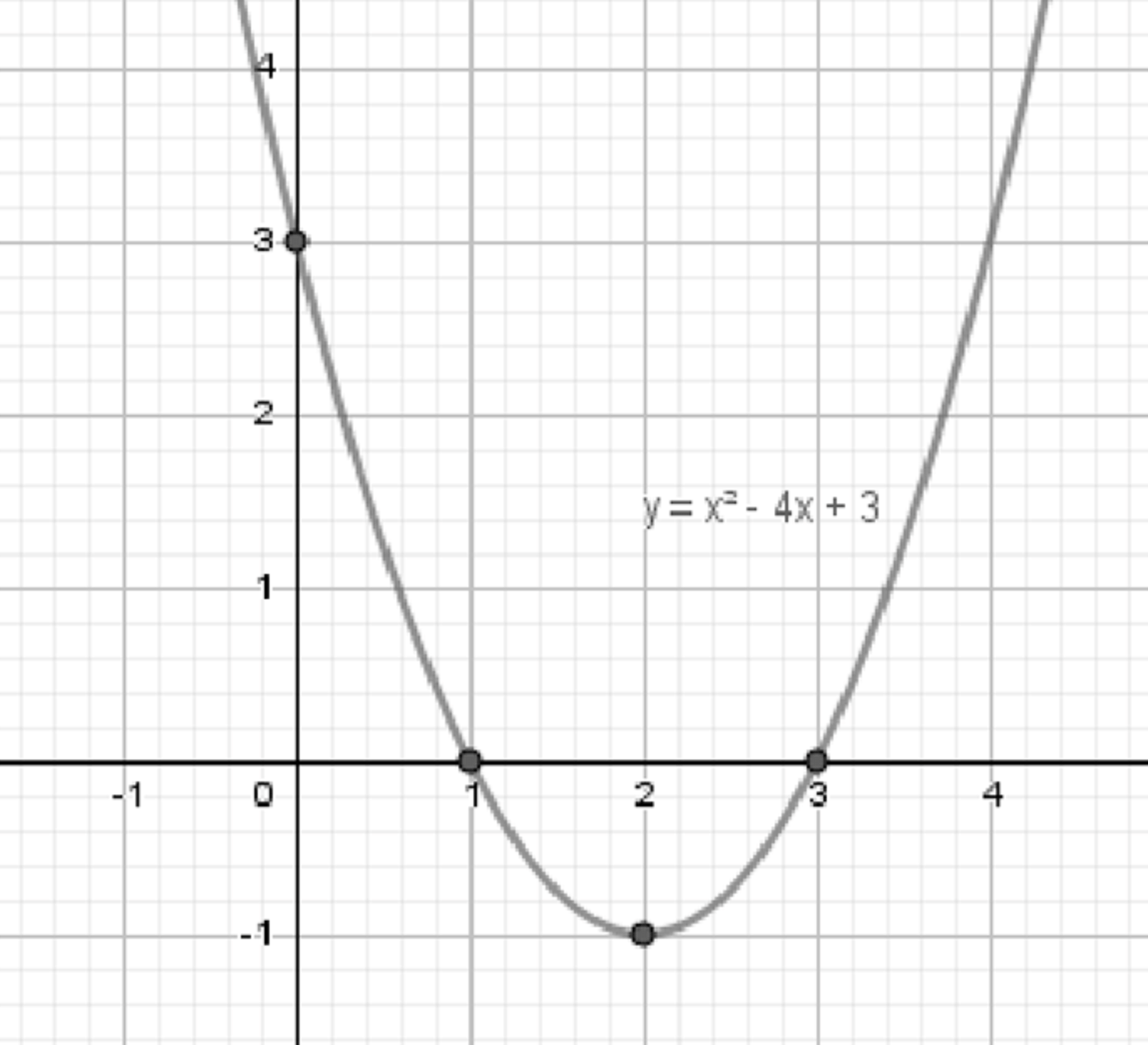
Используя график функции у = f(x), где f(x) = х² — 4х + 3, постройте график функции:

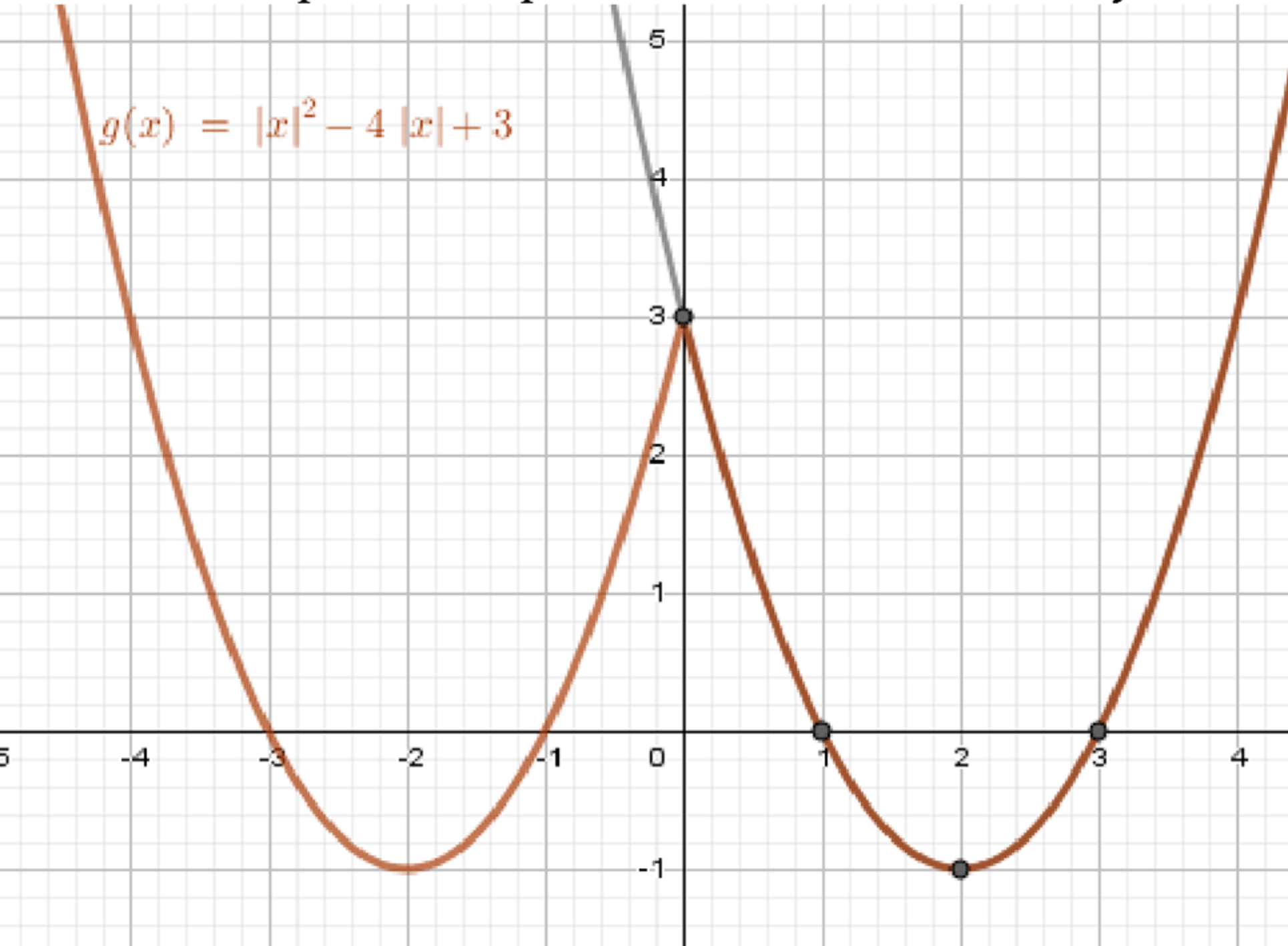
а) у = f(|х|);

б) у = |f(x)|;

в) y = |f(|x|)|;

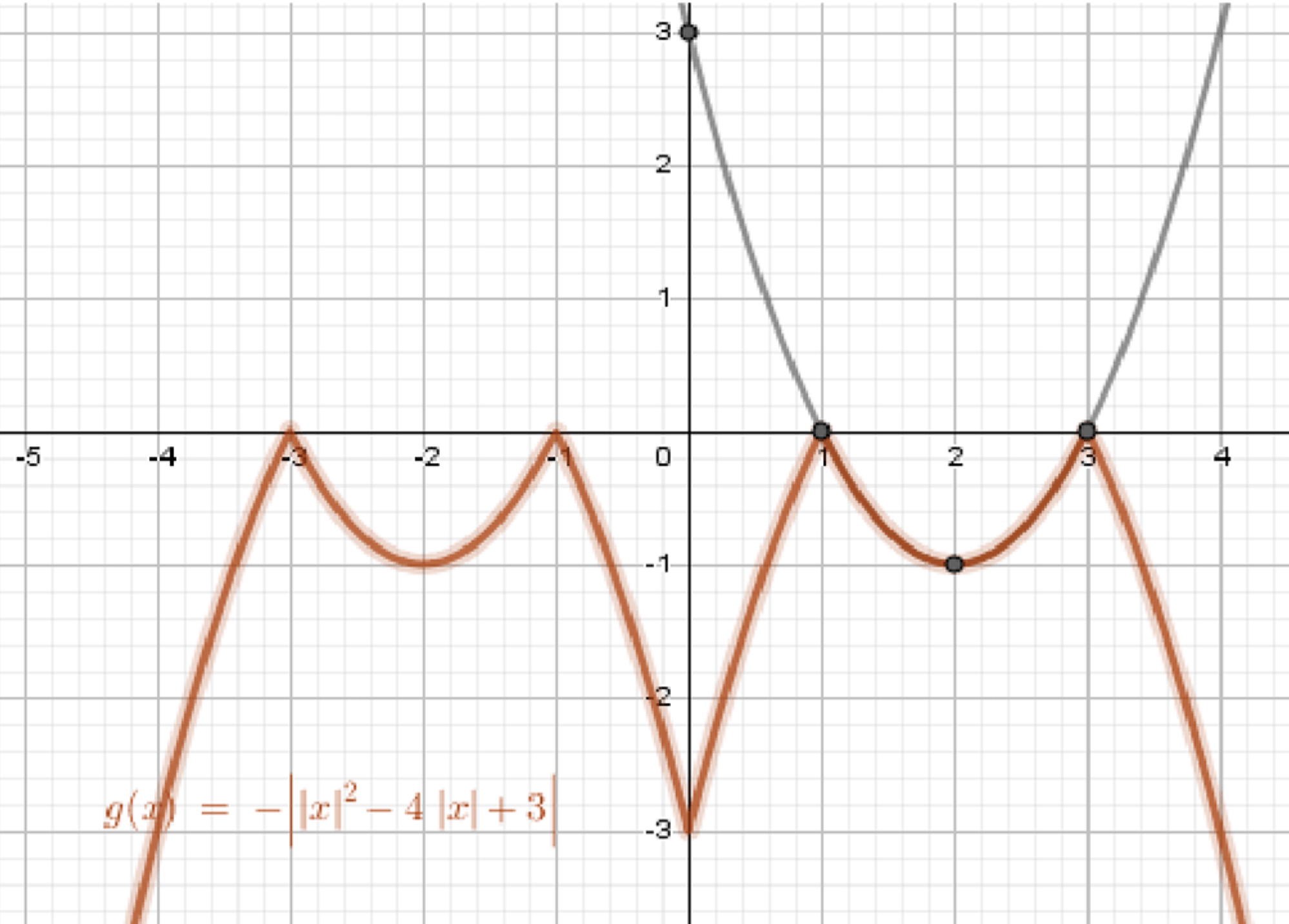
г) у = -|f(|x|)|.

Построим график функции $f(x)=x^2-4x+3$:

$$x_0=-\frac{b}{2a}=-\frac{-4}{2\cdot 1}=\frac{4}{2}=2;$$$$y_0=4-8+3=-1;$$

График функции:

а) $y=f(\mathrm{\mid }x\mathrm{\mid })$:

Уберем часть графика слева от оси ординат;
Отразим его относительно оси ординат:

б) $y=\mathrm{\mid }f(x)\mathrm{\mid }$:

Отразим часть графика снизу от оси абсцисс:

в) $y=\mathrm{\mid }f(\mathrm{\mid }x\mathrm{\mid })\mathrm{\mid }$:

Отразим часть графика снизу от оси абсцисс;
Уберем часть графика слева от оси ординат;
Отразим его относительно оси ординат:

г) $y=-\mathrm{\mid }f(\mathrm{\mid }x\mathrm{\mid })\mathrm{\mid }$:

Отразим часть графика снизу от оси абсцисс;
Уберем часть графика слева от оси ординат;
Отразим его относительно оси ординат;
Отразим его относительно оси абсцисс:

Построение графика функции $f(x)=x^2-4x+3$

Шаг 1. Нахождение вершины параболы

Функция $f(x)=x^2-4x+3$ — это квадратичная функция, и её график представляет собой параболу.

Для нахождения вершины параболы используем формулу для абсциссы вершины:

$$x_0=-\frac{b}{2a},$$

где $a=1$, $b=-4$ — коэффициенты при $x^2$ и $x$ в уравнении.

Подставляем значения:

$$x_0=-\frac{-4}{2\cdot 1}=\frac{4}{2}=2.$$

Теперь находим ординату вершины. Для этого подставляем $x_0=2$ в исходное уравнение:

$$y_0=f(2)=2^2-4\cdot 2+3=4-8+3=-1.$$

Таким образом, вершина параболы находится в точке $(2,-1)$.

Шаг 2. Построение таблицы значений функции

Чтобы построить график, необходимо выбрать несколько значений $x$ и вычислить соответствующие значения $y=f(x)$. В таблице ниже приведены некоторые точки функции:

Значения $y$ вычисляются подстановкой $x$ в исходную функцию $f(x)=x^2-4x+3$:

• Для $x=3$: $y=3^2-4\cdot 3+3=9-12+3=0$.
• Для $x=4$: $y=4^2-4\cdot 4+3=16-16+3=3$.
• Для $x=5$: $y=5^2-4\cdot 5+3=25-20+3=8$.

Шаг 3. Построение графика

Используя найденные точки $(3,0)$, $(4,3)$, $(5,8)$ и вершину $(2,-1)$, строим график функции $y=f(x)$, который представляет собой параболу с ветвями, направленными вверх.

График функции:

а) $y=f(\mathrm{\mid }x\mathrm{\mid })$

Интерпретация:

Функция $y=f(\mathrm{\mid }x\mathrm{\mid })$ означает, что для всех значений $x$, которые меньше нуля, значение функции будет вычисляться как для положительного $x$. Это означает, что график функции будет симметричен относительно оси ординат. То есть для $x<0$ график будет зеркально отражён от графика функции $y=f(x)$, а для $x\ge 0$ график останется неизменным.

Шаги:

1. Мы убираем часть графика, которая находится слева от оси ординат, так как $f(x)$ для отрицательных значений $x$ будет равно $f(-x)$.
2. Отражаем правую часть графика относительно оси ординат, чтобы график стал симметричным.

График:

б) $y=\mathrm{\mid }f(x)\mathrm{\mid }$

Интерпретация:

Функция $y=\mathrm{\mid }f(x)\mathrm{\mid }$ означает, что все отрицательные значения функции $f(x)$ превращаются в положительные. То есть все точки графика, где $f(x)$ отрицательно, будут отражены относительно оси абсцисс.

Шаги:

1. Рассматриваем график функции $y=f(x)$.
2. Для всех значений $x$, где $f(x)<0$, отражаем их относительно оси абсцисс, превращая их в положительные значения.

График:

в) $y=\mathrm{\mid }f(\mathrm{\mid }x\mathrm{\mid })\mathrm{\mid }$

Интерпретация:

Функция $y=\mathrm{\mid }f(\mathrm{\mid }x\mathrm{\mid })\mathrm{\mid }$ — это комбинация двух операций:

1. Мы сначала применяем операцию $f(\mathrm{\mid }x\mathrm{\mid })$, то есть для отрицательных значений $x$ подставляем $\mathrm{\mid }x\mathrm{\mid }$, тем самым делая график симметричным относительно оси ординат.
2. Затем все отрицательные значения, полученные после применения $f(\mathrm{\mid }x\mathrm{\mid })$, превращаются в положительные с помощью операции $\mathrm{\mid }f(x)\mathrm{\mid }$.

Шаги:

1. Убираем часть графика, которая находится слева от оси ординат, и отражаем её относительно оси ординат.
2. Все отрицательные значения на правой части графика превращаем в положительные, отражая их относительно оси абсцисс.

График:

г) $y=-\mathrm{\mid }f(\mathrm{\mid }x\mathrm{\mid })\mathrm{\mid }$

Интерпретация:

Функция $y=-\mathrm{\mid }f(\mathrm{\mid }x\mathrm{\mid })\mathrm{\mid }$ — это комбинация нескольких операций:

1. Сначала применяем $f(\mathrm{\mid }x\mathrm{\mid })$, чтобы сделать график симметричным относительно оси ординат.
2. Применяем операцию $\mathrm{\mid }f(x)\mathrm{\mid }$, чтобы сделать все значения положительными.
3. Затем отражаем весь график относительно оси абсцисс, делая все значения отрицательными.

Шаги:

1. Убираем часть графика слева от оси ординат и отражаем её относительно оси ординат.
2. Все значения функции $f(\mathrm{\mid }x\mathrm{\mid })$ преобразуем в положительные с помощью $\mathrm{\mid }f(x)\mathrm{\mid }$.
3. Отражаем полученную фигуру относительно оси абсцисс, превращая все значения в отрицательные.

График: