Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 1.16 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Решите графически уравнение:
а)
б)
в)
г)
Решить графически уравнение:
а)
- — кубическая парабола:
- — уравнение прямой:
Графики функций:
Ответ: .
б)
- — ветвь параболы:
- — уравнение прямой:
Графики функций:
Ответ: .
в)
- — уравнение ломаной:
- — уравнение гиперболы:
Графики функций:
Ответ: .
г)
- — уравнение гиперболы:
- — уравнение прямой:
Графики функций:
Ответ: .
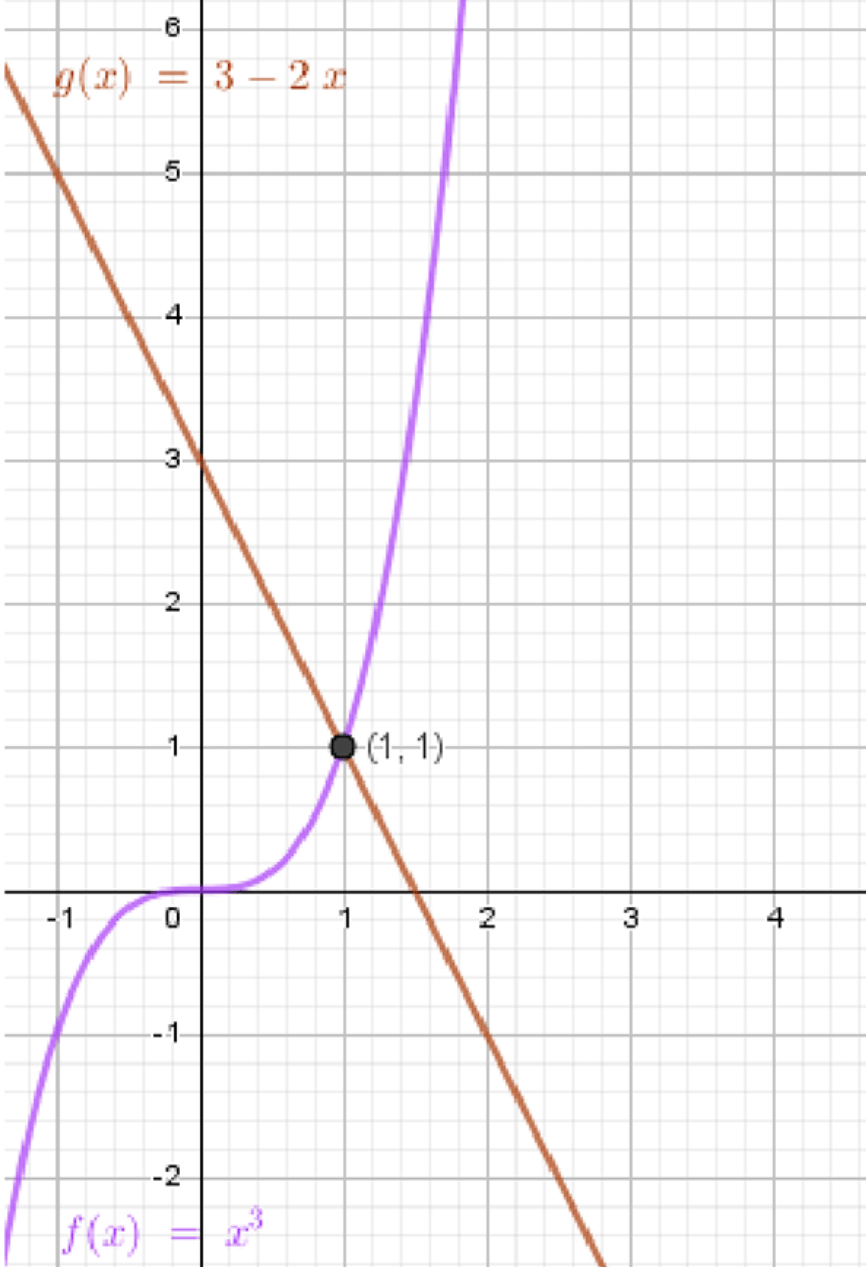
а)
Шаг 1: Преобразуем уравнение
Перепишем уравнение в виде:
Теперь это уравнение можно рассматривать как систему двух функций:
Шаг 2: Построение графиков функций
- График — это кубическая парабола. Она симметрична относительно начала координат, и её вершина находится в точке . Для нескольких точек мы можем вычислить значения функции:
Это даст нам точки и . График будет выглядеть как плавная парабола с ветвями, направленными вверх и вниз.
- График — это прямая. Для неё найдём несколько точек:
Это даёт нам точки и . График будет прямой с углом наклона, направленным вниз.
Шаг 3: Поиск пересечений
Графически решение уравнения соответствует точкам пересечения графиков функций и .
Из графика видно, что графики пересекаются в точке .
Ответ: .
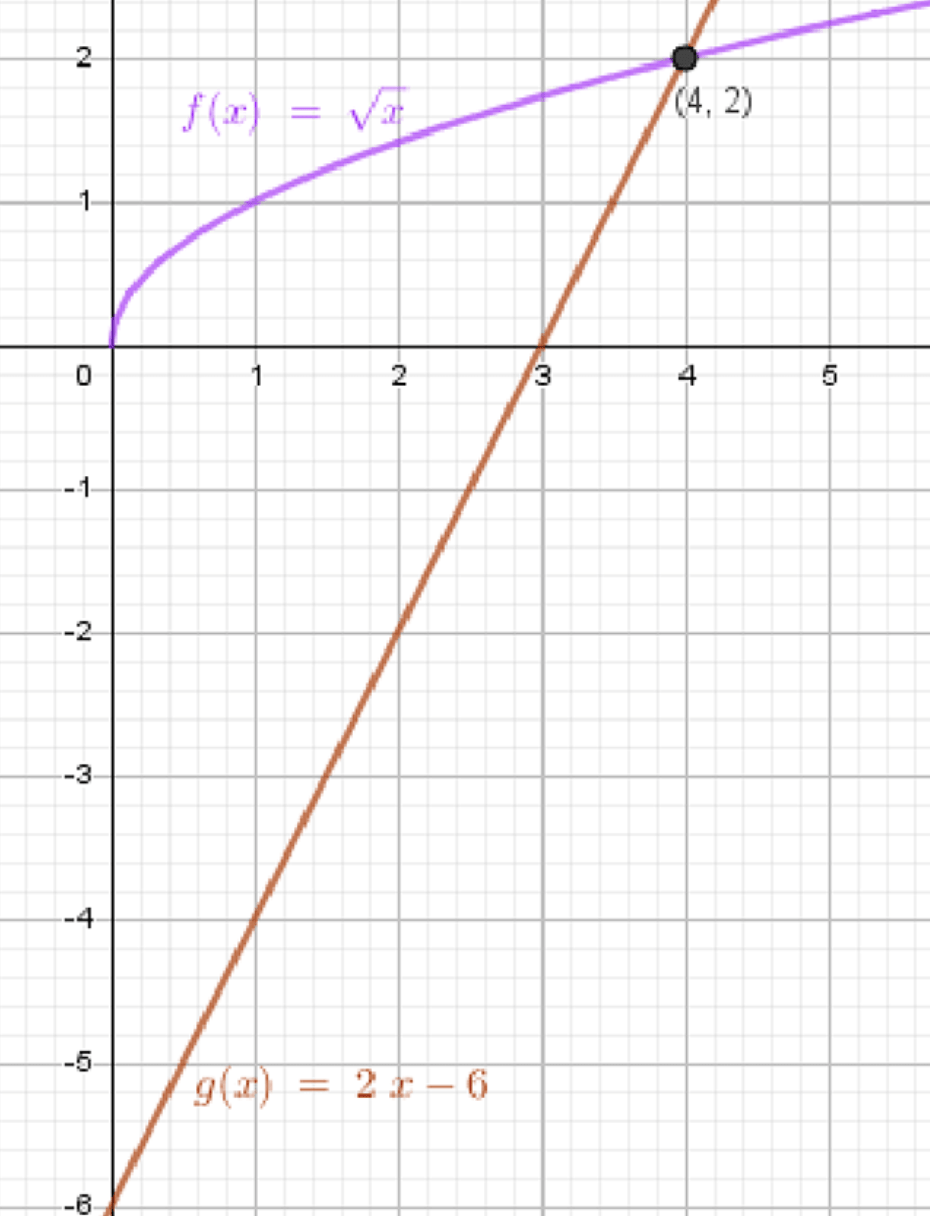
б)
Шаг 1: Преобразуем уравнение
Перепишем уравнение:
Теперь это уравнение можно рассматривать как систему двух функций:
Шаг 2: Построение графиков функций
- График — это ветвь параболы, которая начинается в точке . Для нескольких точек вычислим:
Это даёт нам точки , и . График будет представлять собой кривую, начинающуюся от начала координат и поднимающуюся вверх.
- График — это прямая. Для неё найдём несколько точек:
Это даёт нам точки и . График будет прямой с углом наклона, направленным вверх.
Шаг 3: Поиск пересечений
Графически решение уравнения соответствует точкам пересечения графиков функций и .
Из графика видно, что графики пересекаются в точке .
Ответ: .
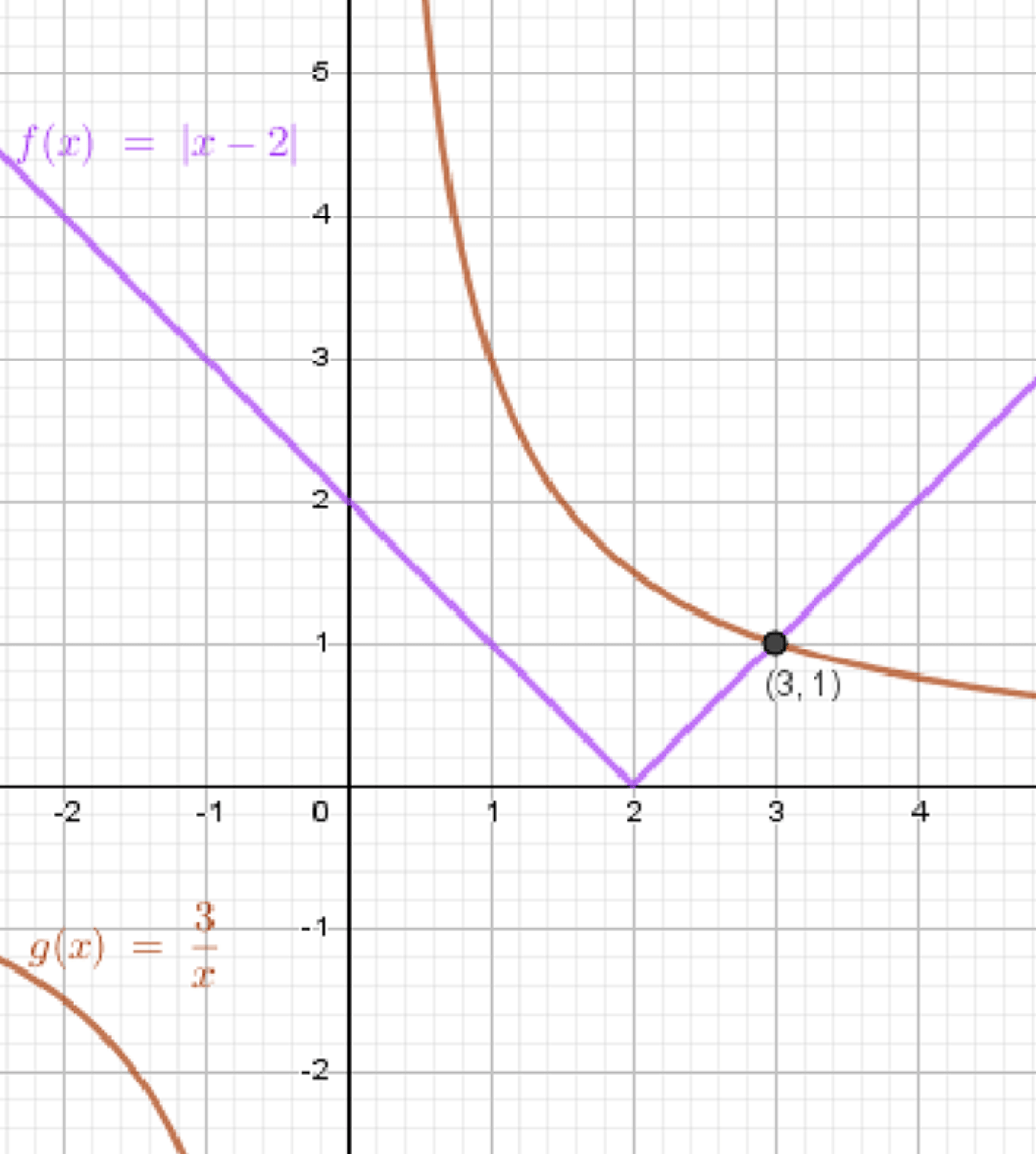
в)
Шаг 1: Преобразуем уравнение
Перепишем уравнение:
Это уравнение можно рассматривать как систему двух функций:
Шаг 2: Построение графиков функций
- График — это ломаная линия, которая имеет точку угла в точке . Для нескольких точек вычислим:
Это даёт нам точки и . График будет выглядеть как буква «V», где вершина находится в точке .
- График — это гипербола. Для неё найдём несколько точек:
Это даёт нам точки и . График будет гиперболой, стремящейся к оси абсцисс и ординат, но никогда их не пересекающей.
Шаг 3: Поиск пересечений
Графически решение уравнения соответствует точкам пересечения графиков функций и .
.
Из графика видно, что графики пересекаются в точке .
Ответ: .
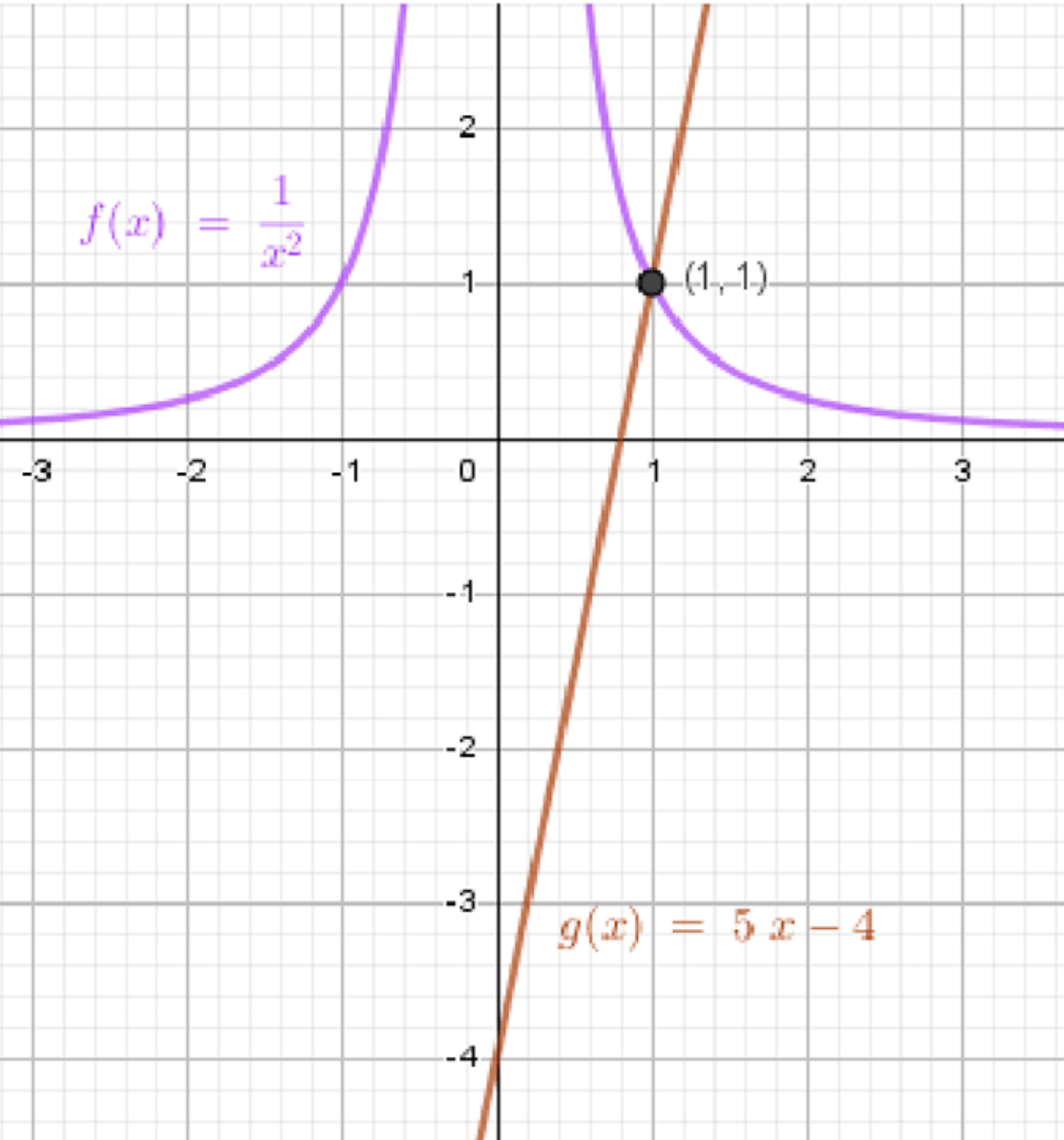
г)
Шаг 1: Преобразуем уравнение
Перепишем уравнение:
Теперь это уравнение можно рассматривать как систему двух функций:
Шаг 2: Построение графиков функций
- График — это гипербола, имеющая вертикальную асимптоту при и горизонтальную асимптоту при . Для нескольких точек вычислим:
Это даёт нам точки и . График будет гиперболой, открывающейся вверх и вправо, стремящейся к асимптотам.
- График — это прямая. Для неё найдём несколько точек:
Это даёт нам точки и . График будет прямой с углом наклона, направленным вверх.
Шаг 3: Поиск пересечений
Графически решение уравнения соответствует точкам пересечения графиков функций и .
Из графика видно, что графики пересекаются в точке .
Ответ: .