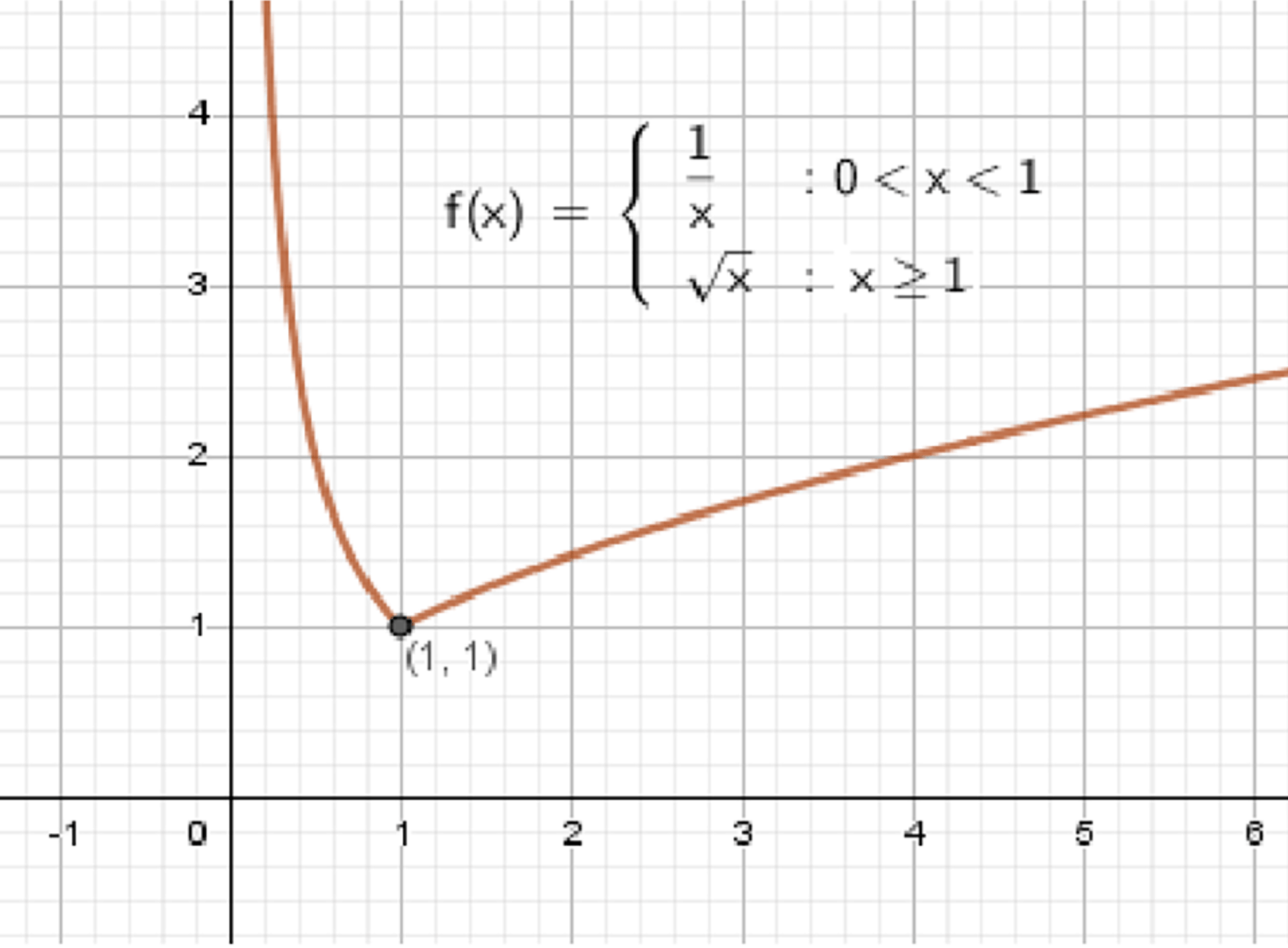ГДЗ 10-11 Класс Номер 1.18 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Дана функция $y=f(x)$, где

$$f(x)=\{\begin{array}{ll}\frac{1}{x},& \text{если }0<x<1,\\ \sqrt{x},& \text{если }x\ge 1.\end{array}$$

а) Найдите $f(6.25)$; $f(0.01)$; $f(-3)$;

б) Постройте график функции;

в) Найдите $D(f)$;

г) Найдите $E(f)$.

Дана функция $f(x)=\{\begin{array}{ll}\frac{1}{x},& \text{если }0<x<1;\\ \sqrt{x},& \text{если }x\ge 1\end{array}$

а) Значения данной функции:

• $f(6,25)=\sqrt{6,25}=2,5$;
• $f(0,01)=\frac{1}{0,01}=100$;
• $f(-3)$ — не существует;

б) $y=\frac{1}{x}$ — уравнение гиперболы:

• $x_0=0$, $y_0=0$;

$y=\sqrt{x}$ — уравнение ветви параболы:

• $x_0=0$, $y_0=0$;

График функции:

в) Область определения:

$D(y)=(0;+\mathrm{\infty });$

г) Множество значений:

$E(y)=[1;+\mathrm{\infty })$

Дана функция $f(x)=\{\begin{array}{ll}\frac{1}{x},& \text{если }0<x<1;\\ \sqrt{x},& \text{если }x\ge 1\end{array}$

а) Значения данной функции

Нужно найти значения функции для различных $x$:

• 1. $f(6.25)$

Поскольку $6.25\ge 1$, то мы используем второй случай из определения функции, который равен $f(x)=\sqrt{x}$.

$$f(6.25)=\sqrt{6.25}=2.5$$

• 2. $f(0.01)$

Поскольку $0.01$ попадает в интервал $0<x<1$, то мы используем первый случай, где $f(x)=\frac{1}{x}$.

$$f(0.01)=\frac{1}{0.01}=100$$

• 3. $f(-3)$

Для $x=-3$, функция не определена, так как для первого случая $0<x<1$, а для второго $x\ge 1$, и ни один из них не покрывает отрицательные значения. Таким образом, $f(-3)$ не существует.

$$f(-3)\text{не существует}\mathrm{.}$$

б) График функции

Чтобы построить график функции, разобьем его на две части в зависимости от того, какой из случаев определяет функцию для каждого $x$.

График для $0<x<1$:

Для этого интервала используется функция $y=\frac{1}{x}$, которая представляет собой гиперболу. Она имеет вертикальную асимптоту в точке $x=0$ и горизонтальную асимптоту в точке $y=0$.

Для некоторых значений $x$:

• При $x=0.5$, $y=\frac{1}{0.5}=2$.
• При $x=1$, $y=\frac{1}{1}=1$.

Таким образом, для $0<x<1$ график будет убывать с бесконечности до точки $(1,1)$, при этом приближаясь к оси $x$ при $x\to 0^{+}$.

График для $x\ge 1$:

Для этого интервала используется функция $y=\sqrt{x}$, которая представляет собой ветвь параболы. График будет начинаться с точки $(1,1)$ и постепенно подниматься вверх.

Для некоторых значений $x$:

• При $x=1$, $y=\sqrt{1}=1$.
• При $x=4$, $y=\sqrt{4}=2$.
• При $x=9$, $y=\sqrt{9}=3$.

Таким образом, для $x\ge 1$ график будет увеличиваться, начиная с точки $(1,1)$, и двигаться вверх, приближаясь к прямой $y=x$.

в) Область определения функции $D(f)$

Область определения функции включает все значения $x$, для которых функция имеет смысл.

1. Для первого случая $f(x)=\frac{1}{x}$, функция определена только при $0<x<1$, так как в $x=0$ функция не существует (деление на ноль).
2. Для второго случая $f(x)=\sqrt{x}$, функция определена при $x\ge 1$, так как квадратный корень из отрицательных чисел не существует в рамках действительных чисел.

Таким образом, область определения функции $D(f)$ — это объединение интервала $(0,1)$ и отрезка $[1,+\mathrm{\infty })$.

$$D(f)=(0;+\mathrm{\infty })$$

г) Множество значений функции $E(f)$

Множество значений функции — это все возможные значения $y$, которые может принимать функция $f(x)$.

1. Для $0<x<1$, функция $f(x)=\frac{1}{x}$ принимает значения от $+\mathrm{\infty }$ до $1$ (при $x\to 0^{+}$, $y\to +\mathrm{\infty }$, и при $x=1$, $y=1$).
2. Для $x\ge 1$, функция $f(x)=\sqrt{x}$ принимает значения от $1$ до $+\mathrm{\infty }$ (при $x=1$, $y=1$, и при $x\to +\mathrm{\infty }$, $y\to +\mathrm{\infty }$).

Таким образом, множество значений функции $E(f)$ — это отрезок $[1,+\mathrm{\infty })$.

$$E(f)=[1;+\mathrm{\infty })$$