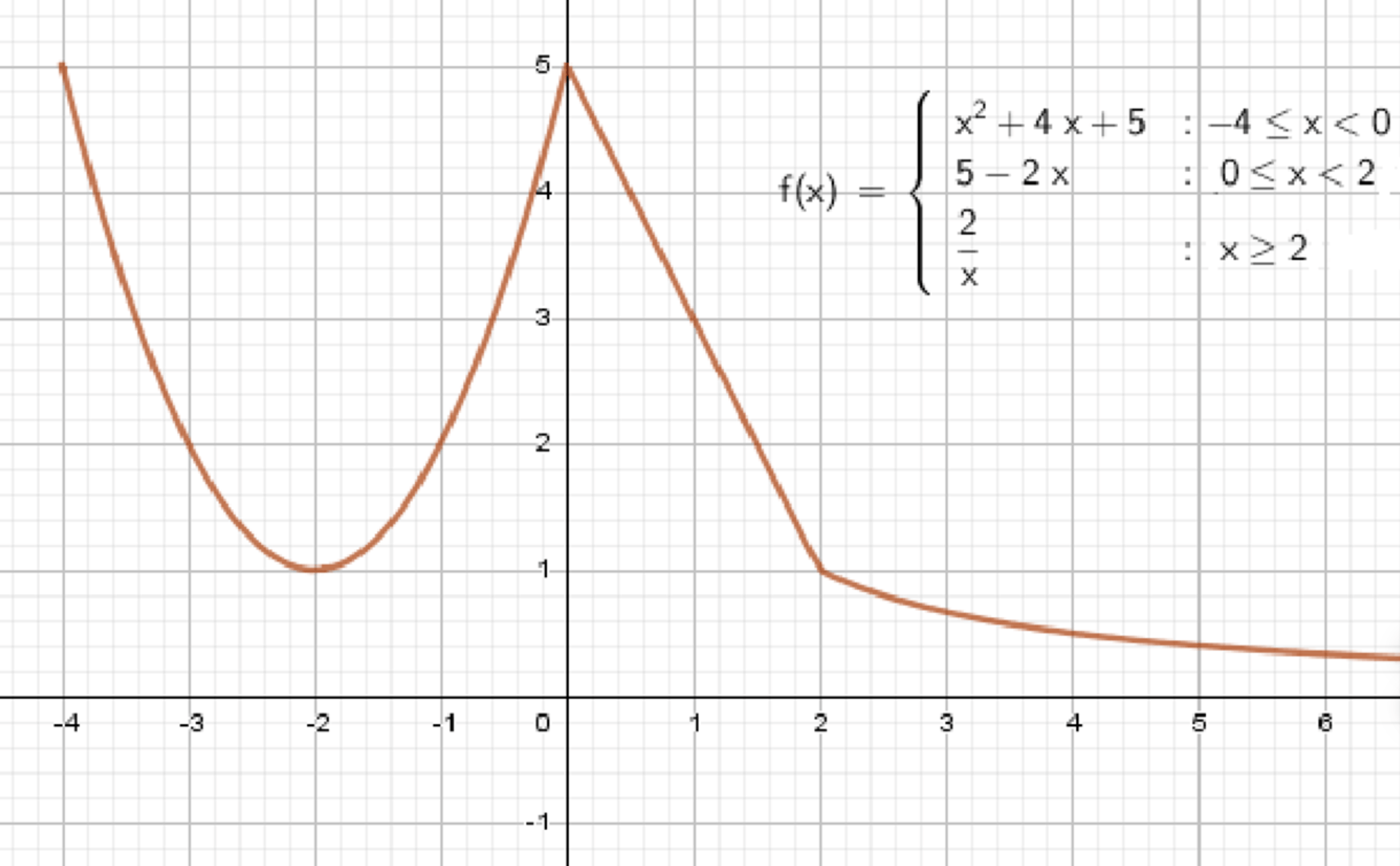ГДЗ 10-11 Класс Номер 1.19 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Дана функция $y=f(x)$, где

$$f(x)=\{\begin{array}{ll}{x}^2+4x+5,& \text{если }-4\le x<0,\\ 5-2x,& \text{если }0\le x<2,\\ \frac{2}{x},& \text{если }x\ge 2.\end{array}$$

а) Найдите $f(-5)$; $f(-3)$; $f(0)$; $f(4)$;

б) Постройте график функции;

в) Найдите $D(f)$;

г) Найдите $E(f)$.

Дана функция $f(x)=\{\begin{array}{ll}{x}^2+4x+5,& \text{если }-4\le x<0\\ 5-2x,& \text{если }0\le x<2\\ \frac{2}{x},& \text{если }x\ge 2\end{array}$

а) Значения данной функции:

• $f(-5)$ — не существует;
• $f(-3)=9-12+5=2$;
• $f(0)=5-2\cdot 0=5$;
• $f(4)=\frac{2}{4}=0.5$;

б) $y=x^2+4x+5$ — уравнение параболы:

• $x_0=-\frac{b}{2a}=-\frac{4}{2\cdot 1}=-\frac{4}{2}=-2$;
• $y_0=(-2{)}^2+4(-2)+5=4-8+5=1$;

$y=5-2x$ — уравнение прямой:

$y=\frac{2}{x}$ — уравнение гиперболы:

• $x_0=0$, $y_0=0$;

График функции:

в) Область определения:

$D(y)=[-4;+\mathrm{\infty });$

г) Множество значений:

$E(y)=(0;5]$

Функция $f(x)$ задана по частям:

$$f(x)=\{\begin{array}{ll}{x}^2+4x+5,& \text{если }-4\le x<0,\\ 5-2x,& \text{если }0\le x<2,\\ \frac{2}{x},& \text{если }x\ge 2.\end{array}$$

а) Найдем значения функции:

Задача состоит в нахождении значений функции для указанных точек: $f(-5)$, $f(-3)$, $f(0)$, $f(4)$.

Найдем $f(-5)$:

$x=-5$ не попадает в область определения для $f(x)$, поскольку $-5$ меньше, чем нижняя граница первого интервала, где $x\ge -4$. Поэтому, $f(-5)$ не существует.

$$f(-5)\text{не существует.}$$

Найдем $f(-3)$:

$x=-3$ попадает в первый интервал, где $-4\le x<0$, и функция определяется как:

$$f(x)=x^2+4x+5.$$

Подставляем $x=-3$:

$$f(-3)=(-3{)}^2+4(-3)+5=9-12+5=2.$$$$f(-3)=2.$$

Найдем $f(0)$:

$x=0$ попадает во второй интервал, где $0\le x<2$, и функция определяется как:

$$f(x)=5-2x\mathrm{.}$$

Подставляем $x=0$:

$$f(0)=5-2\cdot 0=5.$$$$f(0)=5.$$

Найдем $f(4)$:

$x=4$ попадает в третий интервал, где $x\ge 2$, и функция определяется как:

$$f(x)=\frac{2}{x}\mathrm{.}$$

Подставляем $x=4$:

$$f(4)=\frac{2}{4}=\mathrm{0.5.}$$$$f(4)=\mathrm{0.5.}$$

Результат для пункта а):

• $f(-5)$ — не существует;
• $f(-3)=2$;
• $f(0)=5$;
• $f(4)=0.5$.

б) Построение графика функции:

Для первой части функции $f(x)=x^2+4x+5$ на интервале $-4\le x<0$:

Это парабола, открытая вверх, с коэффициентами $a=1$, $b=4$, $c=5$.

• Вершина параболы находится по формуле:$$x_0=-\frac{b}{2a}=-\frac{4}{2\cdot 1}=-2.$$
• Значение функции в вершине:$$y_0=(-2{)}^2+4(-2)+5=4-8+5=1.$$
• Поэтому вершина параболы $(-2,1)$.

Таблица значений:

Для второй части функции $f(x)=5-2x$ на интервале $0\le x<2$:

Это линейная функция с угловым коэффициентом $-2$ и сдвигом по $y$ равным 5.

Таблица значений:

Для третьей части функции $f(x)=\frac{2}{x}$ на интервале $x\ge 2$:

Это гипербола, где $x$ не равен нулю.

Таблица значений:

График функции:

График состоит из трех частей:

• Парабола на интервале $-4\le x<0$,
• Прямая на интервале $0\le x<2$,
• Гипербола на интервале $x\ge 2$.

в) Область определения $D(f)$:

Область определения — это множество значений $x$, для которых функция $f(x)$ имеет смысл. Поскольку $f(x)$ задана на трех интервалах, область определения включает все эти интервалы:

$$D(f)=[-4;+\mathrm{\infty })\mathrm{.}$$

г) Множество значений $E(f)$:

Множество значений функции — это все возможные значения $y$, которые принимает функция $f(x)$.

1. Для первой части функции $f(x)=x^2+4x+5$, $x\in [-4,0)$:Парабола имеет минимальное значение в вершине $x=-2$, где $f(-2)=1$. Поскольку парабола открыта вверх, то значения функции на этом интервале будут больше или равны 1. То есть на интервале $-4\le x<0$ $f(x)\in [1,\mathrm{\infty })$.
2. Для второй части функции $f(x)=5-2x$, $x\in [0,2)$:Линейная функция принимает значения от 5 (при $x=0$) до 1 (при $x=2$), то есть на интервале $[0,2)$ $f(x)\in [1,5)$.
3. Для третьей части функции $f(x)=\frac{2}{x}$, $x\in [2,\mathrm{\infty })$:Гипербола на этом интервале принимает значения от 1 (при $x=2$) до $0$ (при $x\to \mathrm{\infty }$), то есть на интервале $[2,\mathrm{\infty })$ $f(x)\in (0,1]$.

Таким образом, объединяя все эти интервалы, получаем, что множество значений функции $f(x)$:

$$E(f)=(0;5]\mathrm{.}$$