ГДЗ 10-11 Класс Номер 1.8 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график заданной функции, найдите область определения и область значений функции:

а) $y=x^2+2$;

б) $y=3-2x^2$;

в) $y=\frac{1}{2}{x}^2-4$;

г) $y=-1,5x^2-2$

Построить график заданной функции, найти область определения и область значений функции:

а) $y=x^2+2$;

• Построим график функции $y=x^2$;
• Перенесем его на 2 единицы вверх:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty })$; $E(y)=[2;+\mathrm{\infty })$.

б) $y=3-2x^2$;

• Построим график функции $y=-x^2$;
• Растянем его в 2 раза от оси абсцисс;
• Перенесем его на 3 единицы вверх:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty })$; $E(y)=(-\mathrm{\infty };3]$.

в) $y=\frac{1}{2}{x}^2-4$;

• Построим график функции $y=x^2$;
• Сожмем его в 2 раза к оси абсцисс;
• Перенесем его на 4 единицы вниз:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty })$; $E(y)=[-4;+\mathrm{\infty })$.

г) $y=-1,5x^2-2$;

• Построим график функции $y=-x^2$;
• Растянем его в 1,5 раза от оси абсцисс;
• Перенесем его на 2 единицы вниз:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty })$; $E(y)=(-\mathrm{\infty };-2]$.

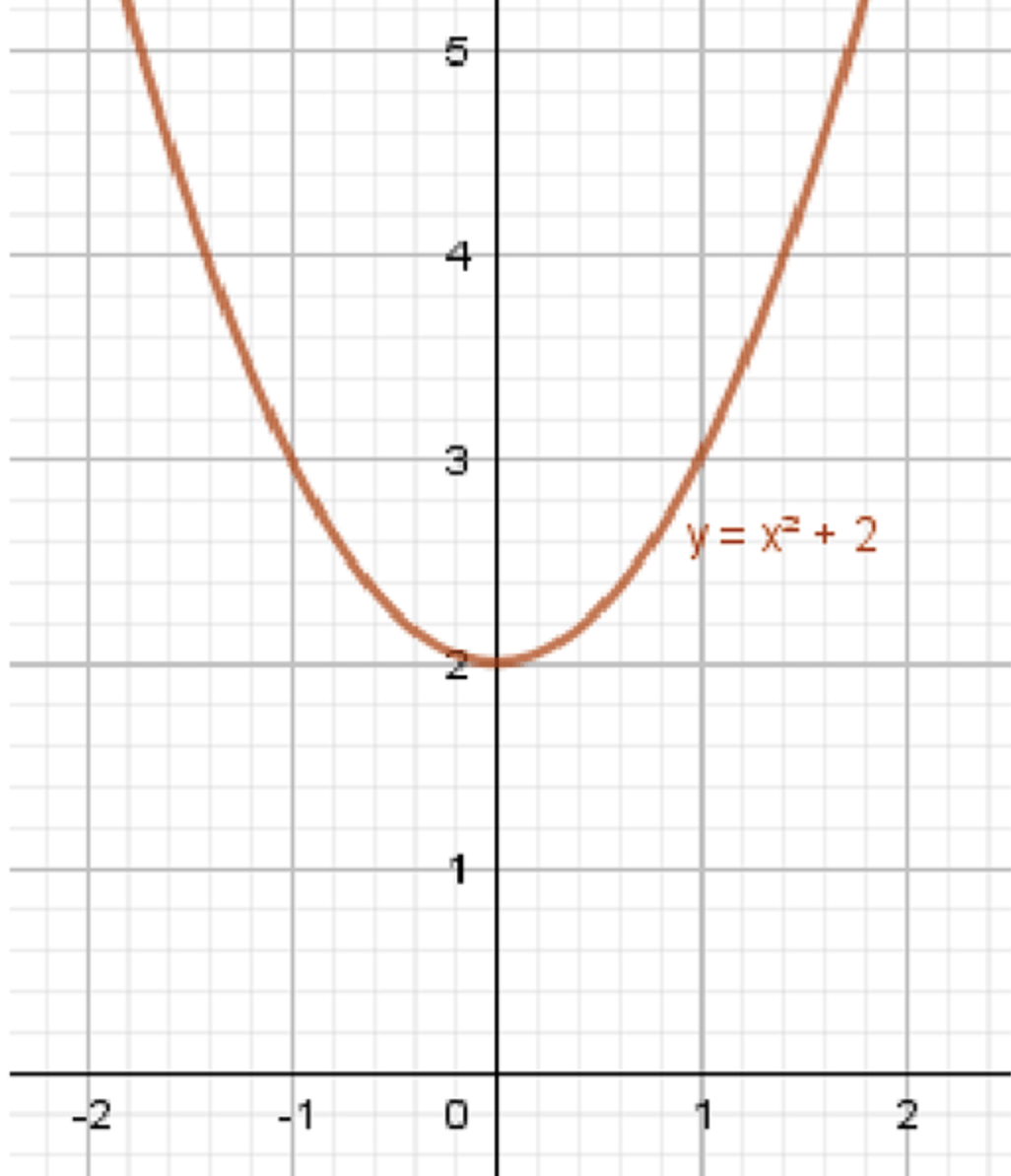
а) $y=x^2+2$

Шаг 1: Область определения (D).

Функция $y=x^2+2$ является квадратичной. Для квадратичных функций область определения всегда будет $(-\mathrm{\infty };+\mathrm{\infty })$, так как они определены для всех значений $x$. Область определения:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Шаг 2: Область значений (E).

Для нахождения области значений рассмотрим график функции. Эта функция представляет собой параболу, которая открывается вверх (так как коэффициент при $x^2$ положительный). Минимальное значение функции будет на вершине параболы, а затем значения $y$ будут увеличиваться без ограничений.

1. Вершина параболы. Для функции $y=x^2+2$ вершина будет в точке, где $x=0$ (так как для квадратичной функции с коэффициентом $x^2=1$ вершина находится в начале координат). Подставляем $x=0$:$$y=0^2+2=2$$

   Следовательно, минимальное значение $y$ равно 2.

2. Так как функция открывается вверх, все значения $y$ будут больше или равны 2. Таким образом, область значений:$$E(y)=[2;+\mathrm{\infty })$$

Шаг 3: Построение графика.

График функции $y=x^2+2$ представляет собой параболу, смещенную на 2 единицы вверх относительно стандартной параболы $y=x^2$. Чтобы построить график, возьмем несколько точек:

• При $x=0$: $y=0^2+2=2$ (точка $(0,2)$)
• При $x=1$: $y=1^2+2=3$ (точка $(1,3)$)
• При $x=-1$: $y=(-1{)}^2+2=3$ (точка $(-1,3)$)
• При $x=2$: $y=2^2+2=6$ (точка $(2,6)$)

График функции будет параболой, открывающейся вверх, с минимальной точкой в $(0,2)$.

График функции:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty })$; $E(y)=[2;+\mathrm{\infty })$.

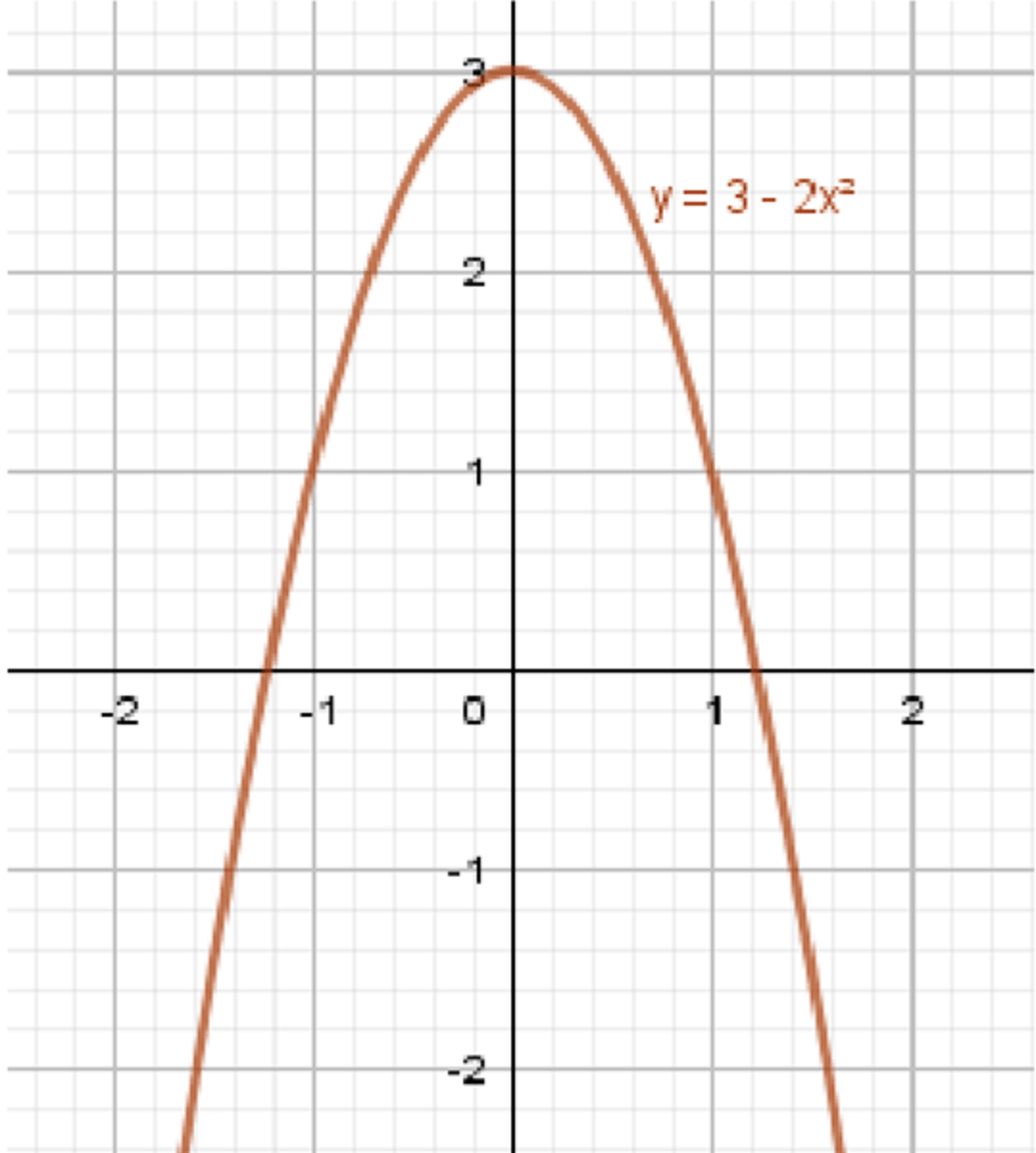
б) $y=3-2x^2$

Шаг 1: Область определения (D).

Функция $y=3-2x^2$ также является квадратичной, и как и в предыдущем примере, область определения для квадратичных функций будет $(-\mathrm{\infty };+\mathrm{\infty })$. Область определения:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Шаг 2: Область значений (E).

Эта функция представляет собой параболу, которая открывается вниз, так как коэффициент при $x^2$ отрицательный ($-2$). Максимальное значение функции будет на вершине параболы.

1. Вершина параболы. Для функции $y=3-2x^2$ вершина будет в точке $x=0$ (по аналогии с предыдущим примером, так как коэффициент при $x^2$ равен $-2$, что не изменяет расположение вершины относительно оси $y$). Подставляем $x=0$:$$y=3-2(0{)}^2=3$$

   Таким образом, максимальное значение $y$ равно 3.

2. Так как парабола открывается вниз, все значения $y$ будут меньше или равны 3. Область значений:$$E(y)=(-\mathrm{\infty };3]$$

Шаг 3: Построение графика.

График функции $y=3-2x^2$ представляет собой параболу, открывающуюся вниз, с максимальной точкой в $(0,3)$. Для построения графика возьмем несколько точек:

• При $x=0$: $y=3-2(0{)}^2=3$ (точка $(0,3)$)
• При $x=1$: $y=3-2(1{)}^2=1$ (точка $(1,1)$)
• При $x=-1$: $y=3-2(-1{)}^2=1$ (точка $(-1,1)$)
• При $x=2$: $y=3-2(2{)}^2=-5$ (точка $(2,-5)$)

График функции будет параболой, открывающейся вниз, с вершиной в $(0,3)$.

График функции:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty })$; $E(y)=(-\mathrm{\infty };3]$.

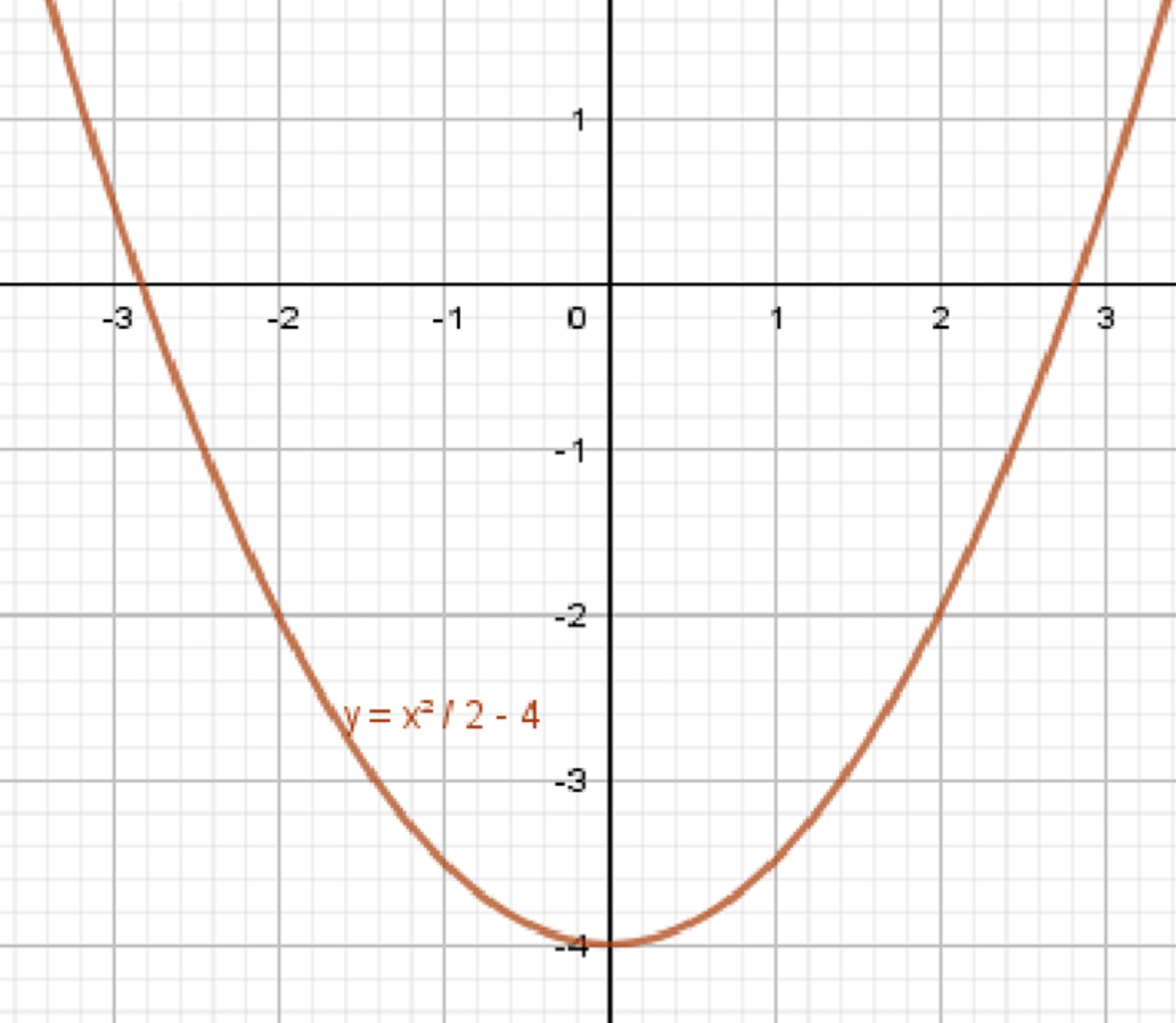
в) $y=\frac{1}{2}{x}^2-4$

Шаг 1: Область определения (D).

Функция $y=\frac{1}{2}{x}^2-4$ является квадратичной. Как и в предыдущих примерах, область определения будет $(-\mathrm{\infty };+\mathrm{\infty })$. Область определения:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Шаг 2: Область значений (E).

Эта функция представляет собой параболу, которая открывается вверх (так как коэффициент при $x^2$ положительный, $\frac{1}{2}$). Минимальное значение функции будет на вершине параболы.

1. Вершина параболы. Для функции $y=\frac{1}{2}{x}^2-4$ вершина будет в точке $x=0$. Подставляем $x=0$:$$y=\frac{1}{2}(0{)}^2-4=-4$$

   Таким образом, минимальное значение $y$ равно -4.

2. Так как функция открывается вверх, все значения $y$ будут больше или равны -4. Область значений:$$E(y)=[-4;+\mathrm{\infty })$$

Шаг 3: Построение графика.

График функции $y=\frac{1}{2}{x}^2-4$ представляет собой параболу, открывающуюся вверх, с минимальной точкой в $(0,-4)$. Для построения графика возьмем несколько точек:

• При $x=0$: $y=\frac{1}{2}(0{)}^2-4=-4$ (точка $(0,-4)$)
• При $x=2$: $y=\frac{1}{2}(2{)}^2-4=-2$ (точка $(2,-2)$)
• При $x=-2$: $y=\frac{1}{2}(-2{)}^2-4=-2$ (точка $(-2,-2)$)
• При $x=4$: $y=\frac{1}{2}(4{)}^2-4=4$ (точка $(4,4)$)

График функции будет параболой, открывающейся вверх, с вершиной в $(0,-4)$.

График функции:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty })$; $E(y)=[-4;+\mathrm{\infty })$.

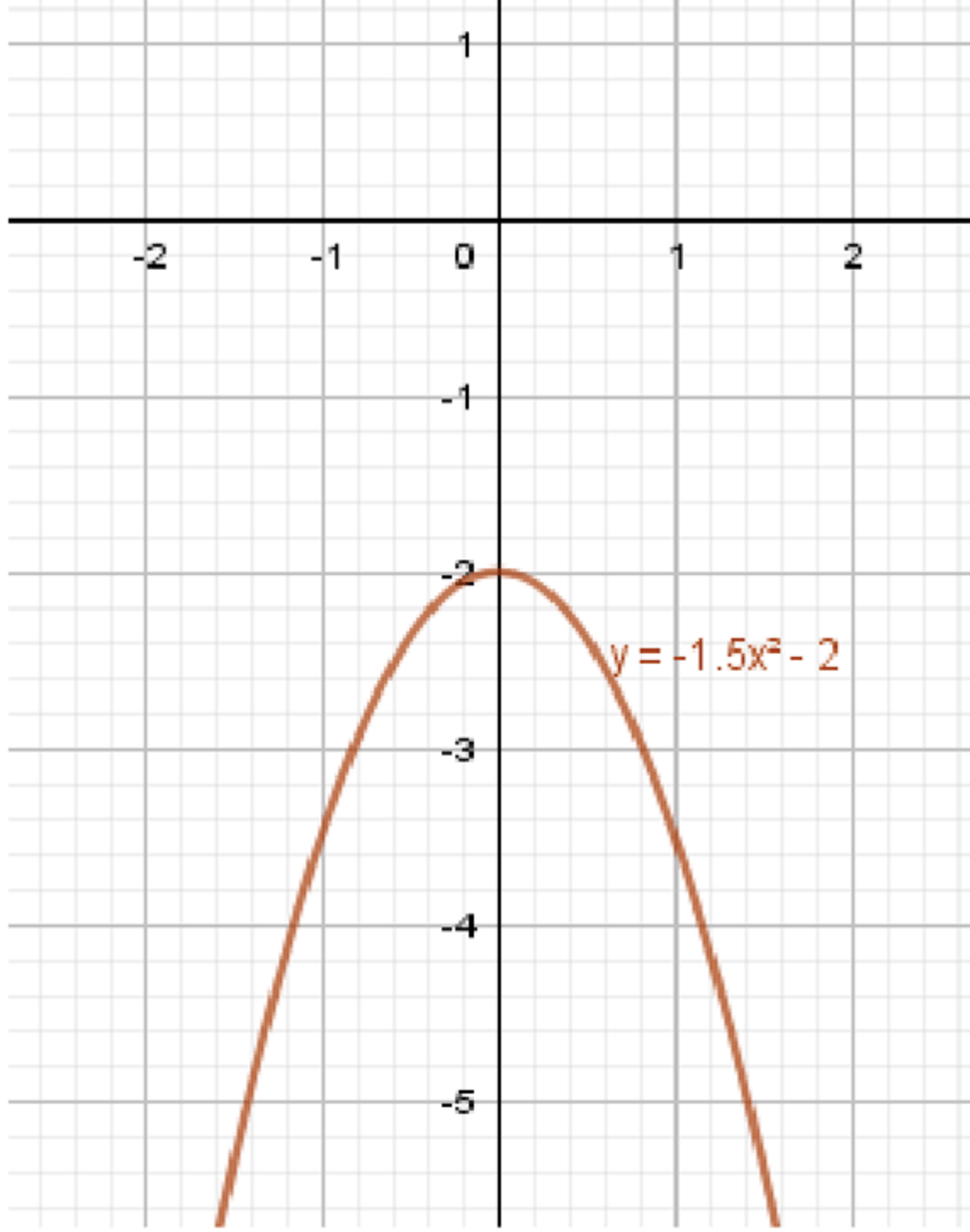
г) $y=-1,5x^2-2$

Шаг 1: Область определения (D).

Функция $y=-1,5x^2-2$ является квадратичной. Как и в других примерах, область определения будет $(-\mathrm{\infty };+\mathrm{\infty })$. Область определения:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Шаг 2: Область значений (E).

Эта функция представляет собой параболу, которая открывается вниз (так как коэффициент при $x^2$ отрицательный, $-1,5$). Максимальное значение функции будет на вершине параболы.

1. Вершина параболы. Для функции $y=-1,5x^2-2$ вершина будет в точке $x=0$. Подставляем $x=0$:$$y=-1,5(0{)}^2-2=-2$$

   Таким образом, максимальное значение $y$ равно -2.

2. Так как парабола открывается вниз, все значения $y$ будут меньше или равны -2. Область значений:$$E(y)=(-\mathrm{\infty };-2]$$

Шаг 3: Построение графика.

График функции $y=-1,5x^2-2$ представляет собой параболу, открывающуюся вниз, с максимальной точкой в $(0,-2)$. Для построения графика возьмем несколько точек:

• При $x=0$: $y=-1,5(0{)}^2-2=-2$ (точка $(0,-2)$)
• При $x=1$: $y=-1,5(1{)}^2-2=-3,5$ (точка $(1,-3,5)$)
• При $x=-1$: $y=-1,5(-1{)}^2-2=-3,5$ (точка $(-1,-3,5)$)
• При $x=2$: $y=-1,5(2{)}^2-2=-8$ (точка $(2,-8)$)

График функции будет параболой, открывающейся вниз, с вершиной в $(0,-2)$.

График функции:

Ответ: $D(y)=(-\mathrm{\infty };+\mathrm{\infty })$; $E(y)=(-\mathrm{\infty };-2]$.