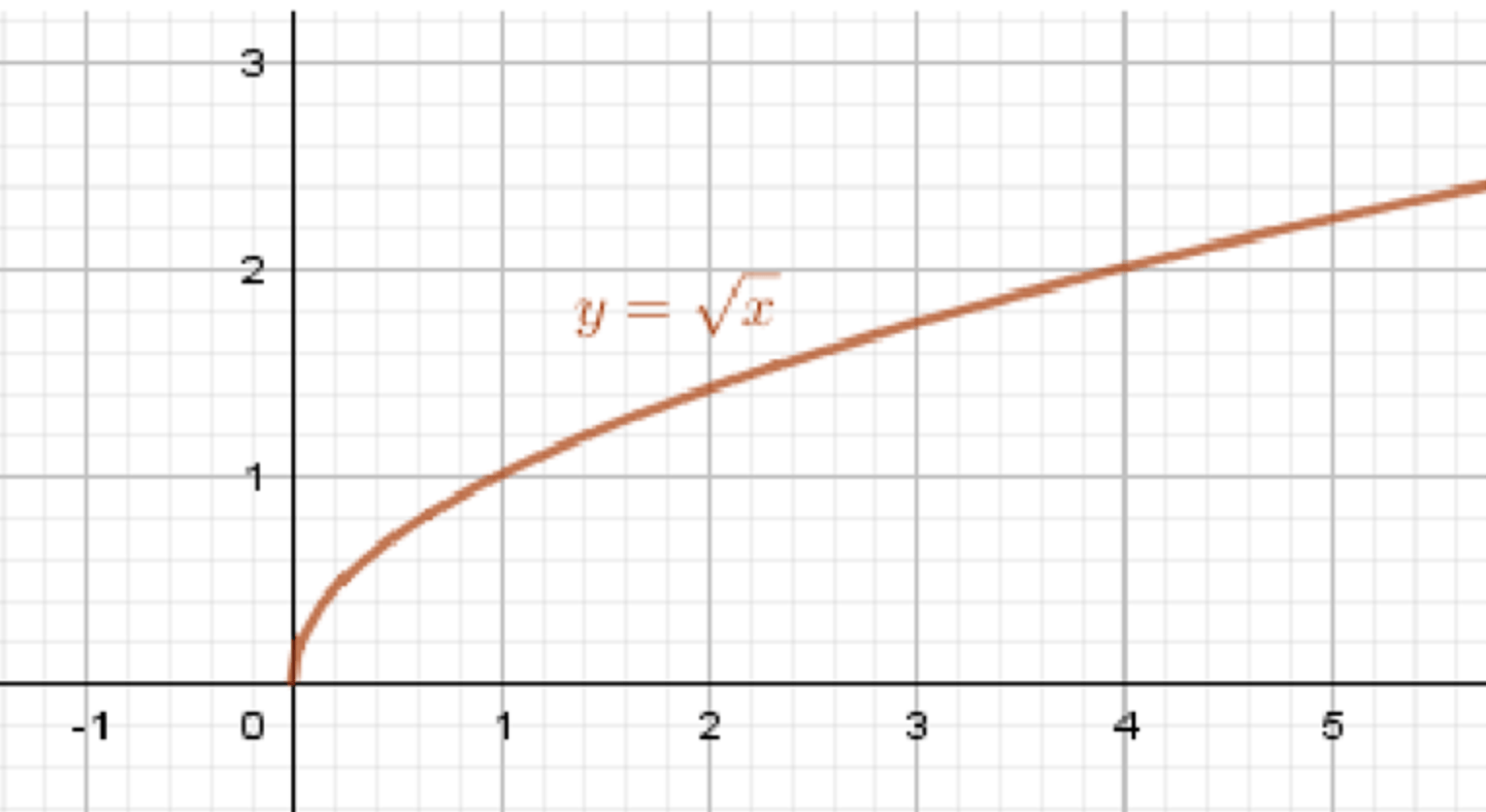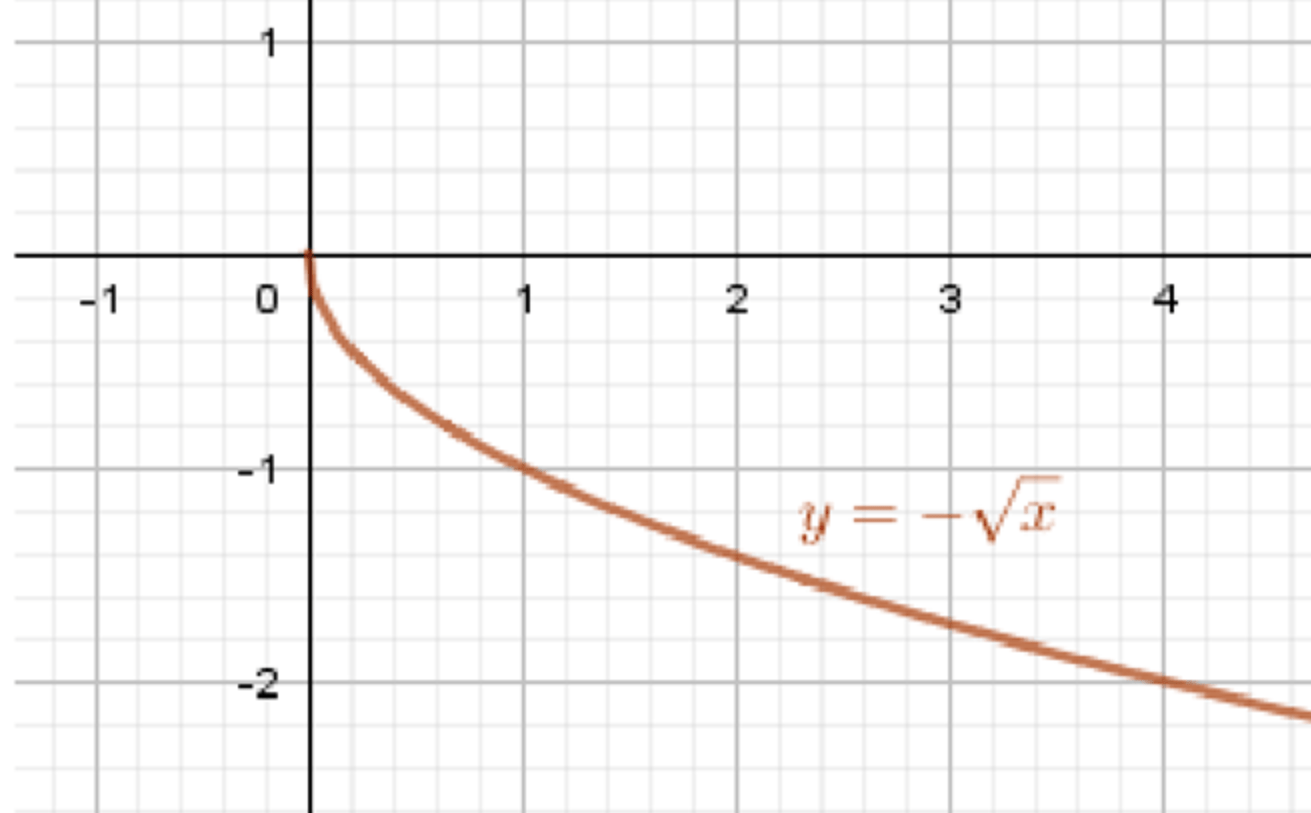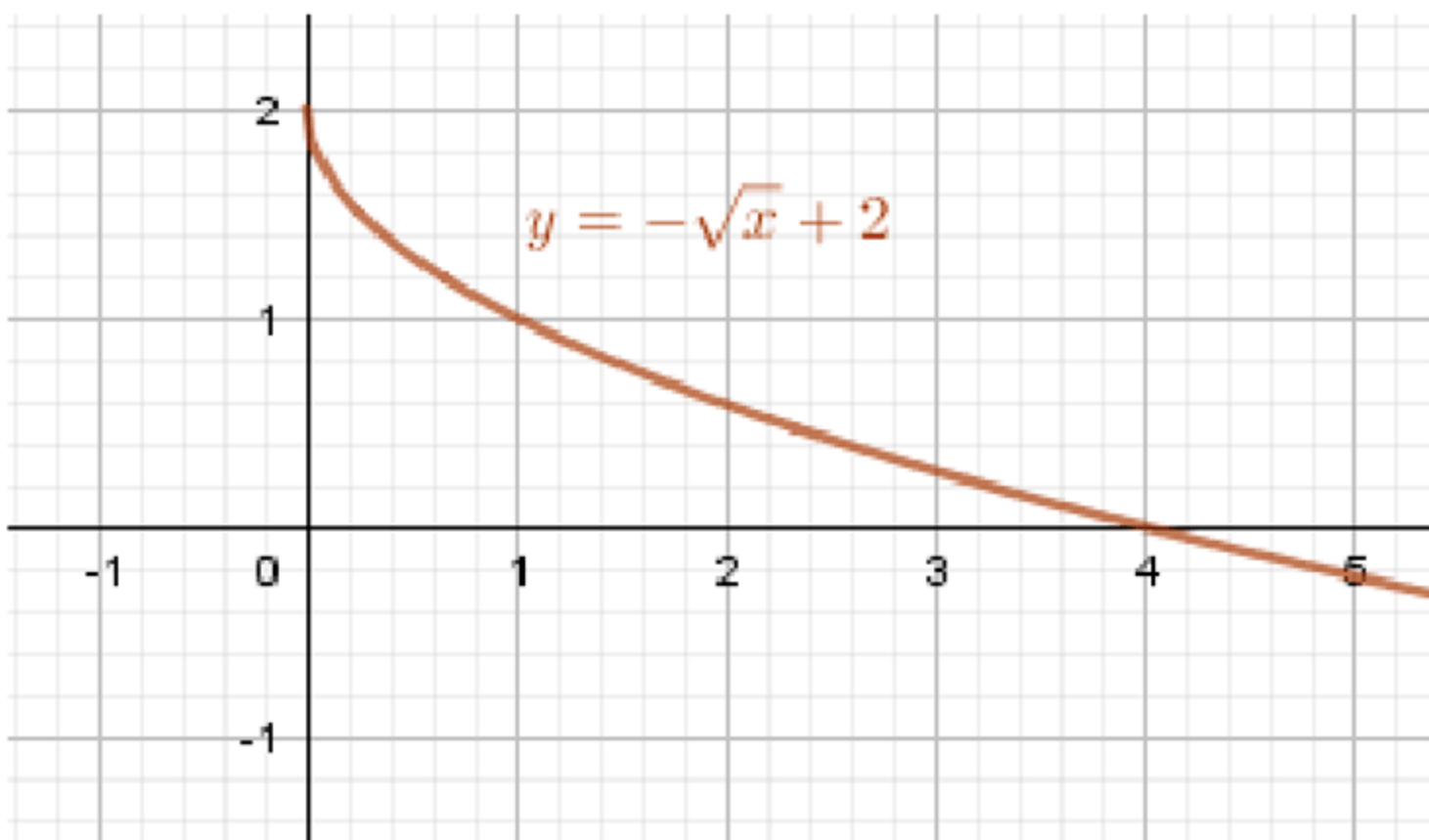Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 1.9 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте график заданной функции, найдите область определения и область значений функции:
а) ;
б) ;
в) ;
г)
Построить график заданной функции, найти область определения и область значений функции:
а) ;
Построим график функции :
Ответ:
;
.
б) ;
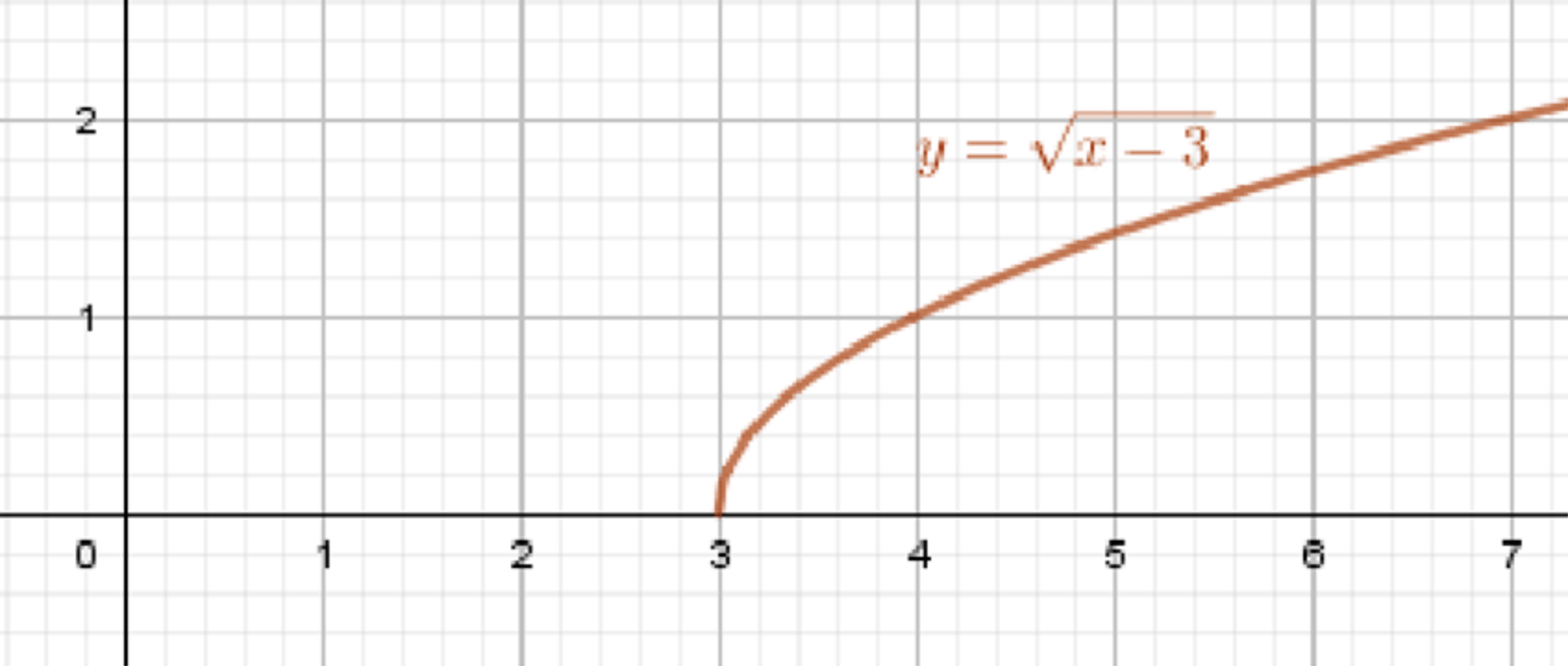
Построим график функции ;
Перенесем его на 3 единицы вправо:
Ответ:
;
.
в) ;
Построим график функции ;
Отразим его относительно оси абсцисс:
Ответ:
;
.
г) ;
Построим график функции ;
Отразим его относительно оси абсцисс;
Перенесем его на 2 единицы вверх:
Ответ:
;
.
а)
Шаг 1: Область определения
Функция имеет подкоренное выражение , которое должно быть неотрицательным, так как из подкоренного выражения нельзя извлечь квадратный корень из отрицательных чисел (в рамках вещественных чисел). Следовательно, для того чтобы функция была определена, необходимо, чтобы .
Таким образом, область определения функции:
Шаг 2: Область значений
Функция для принимает только неотрицательные значения. При функция даёт значение . По мере увеличения значение функции также будет увеличиваться. Таким образом, область значений функции:
Шаг 3: Построение графика
График функции представляет собой кривую, которая начинается в точке и увеличивается по мере увеличения . График будет плавно возрастать, так как функция растёт медленно (корень из числа растёт медленно с увеличением ).
График функции:
Ответ:
б)
Шаг 1: Область определения
Функция имеет подкоренное выражение , которое должно быть неотрицательным, так как из подкоренного выражения нельзя извлечь квадратный корень из отрицательных чисел. Для того чтобы функция была определена, необходимо, чтобы:
Решая это неравенство:
Таким образом, область определения функции:
Шаг 2: Область значений
Для функция принимает неотрицательные значения. Когда , функция даёт значение . По мере увеличения , значение будет увеличиваться. Следовательно, область значений:
Шаг 3: Построение графика
График функции будет выглядеть аналогично графику , но сдвинутым на 3 единицы вправо. То есть, вместо того чтобы начинаться с точки , график начнётся в точке и будет возрастать по мере увеличения .
График функции:
Ответ:
в)
Шаг 1: Область определения
Функция имеет подкоренное выражение , которое должно быть неотрицательным, так как из подкоренного выражения нельзя извлечь квадратный корень из отрицательных чисел. Следовательно, для того чтобы функция была определена, необходимо, чтобы:
Таким образом, область определения функции:
Шаг 2: Область значений
Функция принимает только отрицательные значения или ноль, так как для всех функция будет иметь значение, равное отрицательному корню из . При , функция даёт . По мере увеличения , будет уменьшаться, так как корень из будет расти, а знак минус перед корнем делает значение функции отрицательным.
Таким образом, область значений:
Шаг 3: Построение графика
График функции представляет собой кривую, которая начинается в точке и убывает по мере увеличения . График будет плавно опускаться, так как корень из растёт медленно, а знак минус делает значения функции отрицательными.
График функции:
Ответ:
г)
Шаг 1: Область определения
Функция имеет подкоренное выражение , которое должно быть неотрицательным, так как из подкоренного выражения нельзя извлечь квадратный корень из отрицательных чисел. Следовательно, для того чтобы функция была определена, необходимо, чтобы:
Таким образом, область определения функции:
Шаг 2: Область значений
Функция имеет форму, аналогичную функции , но сдвинутую на 2 единицы вверх. Это означает, что график функции будет начинаться в точке и будет убывать по мере увеличения , так как знак минус перед корнем делает значения функции отрицательными. При , . По мере увеличения , будет уменьшаться, но оставаться не больше 2.
Таким образом, область значений:
Шаг 3: Построение графика
График функции будет представлять собой параболу, открывающуюся вниз, с вершиной в точке . График будет спадать по мере увеличения .
График функции:
Ответ: