ГДЗ 10-11 Класс Номер 10.10 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Построить график функции:

а) $y = \sin\left(x — \frac{\pi}{4}\right) + 1$;

Построим график функции $y = \sin x$;
Переместим его на $\frac{\pi}{4}$ единицы вправо;
Переместим его на 1 единицу вверх:

б) $y = \sin\left(x + \frac{\pi}{3}\right) — 1$;

Построим график функции $y = \sin x$;
Переместим его на $\frac{\pi}{3}$ единицы влево;
Переместим его на 1 единицу вниз:

База: сдвиги у $y=\sin(x-s)+d$

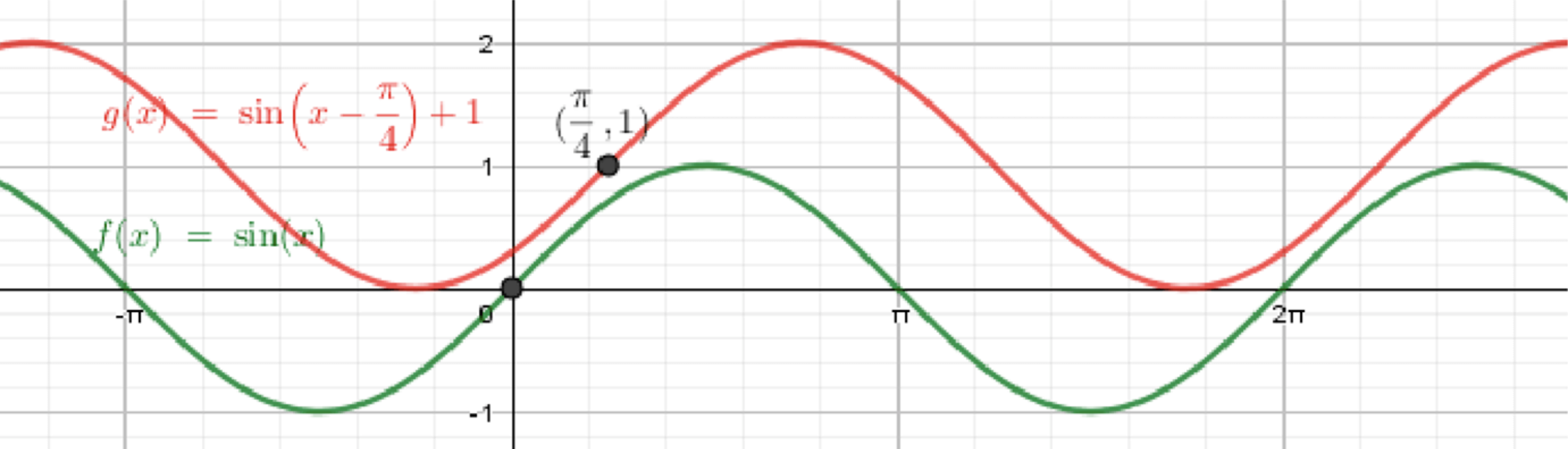
• Область определения: все $x\in\mathbb{R}$.
• Период: $2\pi$ (не меняется при сдвигах).
• Амплитуда: $1$ (здесь растяжений нет).
• Горизонтальный сдвиг: $x\mapsto x-s$ — вправо на $s$ (если $s>0$), влево (если $s<0$).
• Вертикальный сдвиг: вверх на $d$ (если $d>0$), вниз (если $d<0$).
• Средняя линия: $y=d$.
• Значения: $[d-1,\ d+1]$.
• Экстремумы (для всех $k\in\mathbb{Z}$):
  • максимумы при $x=s+\tfrac{\pi}{2}+2\pi k,\quad y=d+1$;
  • минимумы при $x=s+\tfrac{3\pi}{2}+2\pi k,\quad y=d-1$.
• Производная: $y’=\cos(x-s)$.
  Возрастает на $\big(s-\tfrac{\pi}{2}+2\pi k,\ s+\tfrac{\pi}{2}+2\pi k\big)$, убывает на $\big(s+\tfrac{\pi}{2}+2\pi k,\ s+\tfrac{3\pi}{2}+2\pi k\big)$.
• Вторая производная: $y»=-\sin(x-s)$.
  Ветви вниз (выпуклость вниз), когда $\sin(x-s)>0$ — т.е. $x\in(s,\ s+\pi)+2\pi k$; вверх, когда $\sin(x-s)<0$ — $x\in(s+\pi,\ s+2\pi)+2\pi k$.
• «Пятиточечный шаблон» одного периода (в координатах $x$):
  $x=s+0,\ s+\tfrac{\pi}{2},\ s+\pi,\ s+\tfrac{3\pi}{2},\ s+2\pi$ с $y=d,\ d+1,\ d,\ d-1,\ d$.

а) $y=\sin\!\Big(x-\tfrac{\pi}{4}\Big)+1$

Параметры. $s=\tfrac{\pi}{4}$ (вправо на $\tfrac{\pi}{4}$); $d=1$ (вверх на 1).
Период $2\pi$, амплитуда $1$, средняя линия $y=1$, диапазон значений $[0,2]$.

Ключевые уровни: вершины $y=2$, впадины $y=0$.

Опорные точки (шаблон, подставили $s,d$):

$$\begin{aligned} x&=\tfrac{\pi}{4} &&\Rightarrow\ y=1,\\ x&=\tfrac{3\pi}{4} &&\Rightarrow\ y=2,\\ x&=\tfrac{5\pi}{4} &&\Rightarrow\ y=1,\\ x&=\tfrac{7\pi}{4} &&\Rightarrow\ y=0,\\ x&=\tfrac{9\pi}{4} &&\Rightarrow\ y=1\ (\text{уже за }2\pi). \end{aligned}$$

Для отрезка $[0,2\pi]$ используйте четыре первые.

Экстремумы (все $k\in\mathbb{Z}$):

• максимумы: $x=\tfrac{\pi}{4}+\tfrac{\pi}{2}+2\pi k=\tfrac{3\pi}{4}+2\pi k,\ y=2$;
• минимумы: $x=\tfrac{\pi}{4}+\tfrac{3\pi}{2}+2\pi k=\tfrac{7\pi}{4}+2\pi k,\ y=0$.

Пересечения с осями.

• С $Oy$: $x=0\Rightarrow y=\sin\!\big(-\tfrac{\pi}{4}\big)+1=1-\tfrac{\sqrt{2}}{2}\approx0.293$.
• С $Ox$ (нули): $\sin(x-\tfrac{\pi}{4})+1=0\Rightarrow \sin(x-\tfrac{\pi}{4})=-1\Rightarrow x=\tfrac{7\pi}{4}+2\pi k$.
  Это касание оси $Ox$ (в точке минимума; касательная горизонтальна).

Монотонность (в пределах $[0,2\pi]$):

• возрастает на $(0,\ \tfrac{3\pi}{4})$ и $(\tfrac{7\pi}{4},\ 2\pi)$;
• убывает на $(\tfrac{3\pi}{4},\ \tfrac{7\pi}{4})$.

Выпуклость (на $[0,2\pi]$):

• вниз на $\big(\tfrac{\pi}{4},\ \tfrac{5\pi}{4}\big)$;
• вверх на $\big(\tfrac{5\pi}{4},\ 2\pi\big)$.

Как построить (пошагово):

1. Проведите горизонтальную среднюю линию $y=1$. Отметьте уровни $y=2$ и $y=0$.
2. По оси $x$ разметьте точки $\tfrac{\pi}{4},\ \tfrac{3\pi}{4},\ \tfrac{5\pi}{4},\ \tfrac{7\pi}{4},\ 2\pi$.
3. Поставьте опорные точки: $(\tfrac{\pi}{4},1)$, $(\tfrac{3\pi}{4},2)$, $(\tfrac{5\pi}{4},1)$, $(\tfrac{7\pi}{4},0)$.
4. Соедините плавной синусоидой: от $y=1$ (на $\tfrac{\pi}{4}$) вверх до $2$, затем вниз до $1$, далее до $0$ и снова к $1$.
5. Продолжите периодически с шагом $2\pi$ по $x$.

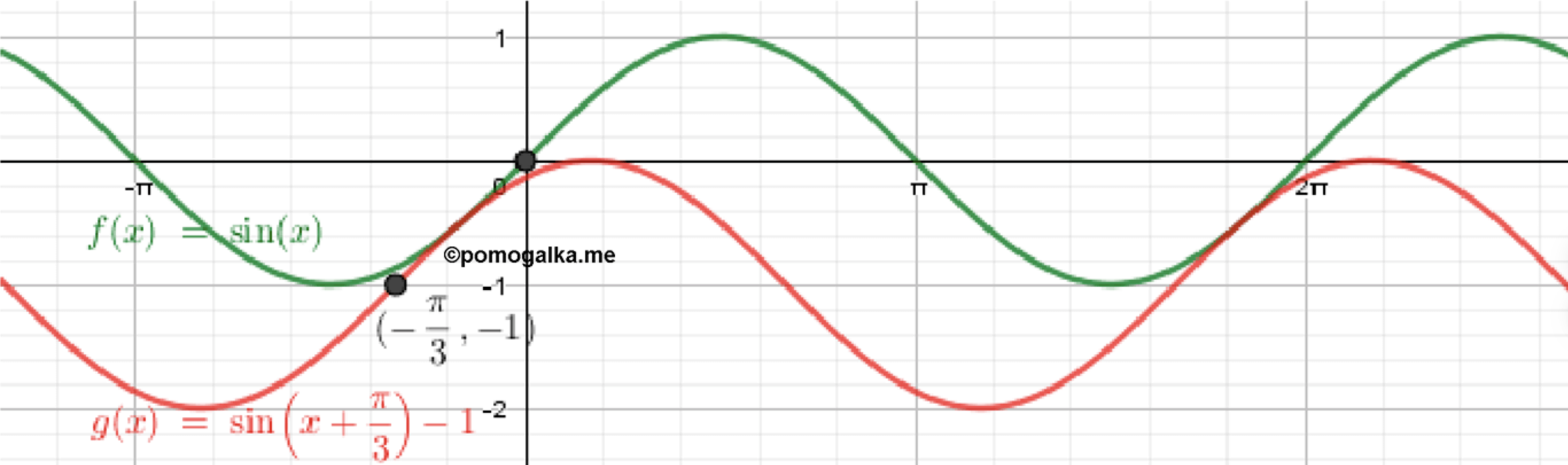
б) $y=\sin\!\Big(x+\tfrac{\pi}{3}\Big)-1$

Параметры. $s=-\tfrac{\pi}{3}$ (влево на $\tfrac{\pi}{3}$); $d=-1$ (вниз на 1).
Период $2\pi$, амплитуда $1$, средняя линия $y=-1$, диапазон значений $[-2,0]$.

Ключевые уровни: вершины $y=0$, впадины $y=-2$.

Опорные точки (используем $t=x+\tfrac{\pi}{3}$, т.е. $x=t-\tfrac{\pi}{3}$):

$$\begin{aligned} x&=-\tfrac{\pi}{3} &&\Rightarrow\ y=-1\ (\text{вне }[0,2\pi]),\\ x&=\tfrac{\pi}{6} &&\Rightarrow\ y=0\ (\text{максимум/касание }Ox),\\ x&=\tfrac{2\pi}{3} &&\Rightarrow\ y=-1,\\ x&=\tfrac{7\pi}{6} &&\Rightarrow\ y=-2\ (\text{минимум}),\\ x&=\tfrac{5\pi}{3} &&\Rightarrow\ y=-1. \end{aligned}$$

На $[0,2\pi]$ удобно брать $\tfrac{\pi}{6},\ \tfrac{2\pi}{3},\ \tfrac{7\pi}{6},\ \tfrac{5\pi}{3}$.

Экстремумы (все $k\in\mathbb{Z}$):

• максимумы: $x=-\tfrac{\pi}{3}+\tfrac{\pi}{2}+2\pi k=\tfrac{\pi}{6}+2\pi k,\ y=0$;
• минимумы: $x=-\tfrac{\pi}{3}+\tfrac{3\pi}{2}+2\pi k=\tfrac{7\pi}{6}+2\pi k,\ y=-2$.

Пересечения с осями.

• С $Oy$: $x=0\Rightarrow y=\sin\!\big(\tfrac{\pi}{3}\big)-1=\tfrac{\sqrt3}{2}-1\approx-0.134$.
• С $Ox$ (нули): $\sin(x+\tfrac{\pi}{3})-1=0\Rightarrow \sin(x+\tfrac{\pi}{3})=1\Rightarrow x=\tfrac{\pi}{6}+2\pi k$.
  Это касание оси $Ox$ в точках максимума (касательная горизонтальна), график не поднимается выше $0$.

Монотонность (на $[0,2\pi]$):

• возрастает на $(0,\ \tfrac{\pi}{6})$ и $(\tfrac{7\pi}{6},\ 2\pi)$;
• убывает на $(\tfrac{\pi}{6},\ \tfrac{7\pi}{6})$.

Выпуклость (на $[0,2\pi]$):

• вниз на $\big(0,\ \tfrac{2\pi}{3}\big)$ и $\big(\tfrac{5\pi}{3},\ 2\pi\big)$;
• вверх на $\big(\tfrac{2\pi}{3},\ \tfrac{5\pi}{3}\big)$.

Как построить (пошагово):

1. Проведите среднюю линию $y=-1$. Отметьте уровни $y=0$ и $y=-2$.
2. По оси $x$ разметьте $\tfrac{\pi}{6},\ \tfrac{2\pi}{3},\ \tfrac{7\pi}{6},\ \tfrac{5\pi}{3},\ 2\pi$.
3. Поставьте опорные точки: максимум $(\tfrac{\pi}{6},0)$, «середины» $(\tfrac{2\pi}{3},-1)$ и $(\tfrac{5\pi}{3},-1)$, минимум $(\tfrac{7\pi}{6},-2)$.
4. Соедините плавной синусоидой: от касания оси $Ox$ опускайтесь к средней линии, далее к минимуму, снова к средней линии.
5. Продолжите периодически с шагом $2\pi$.