Краткий ответ:
Построить график функции:
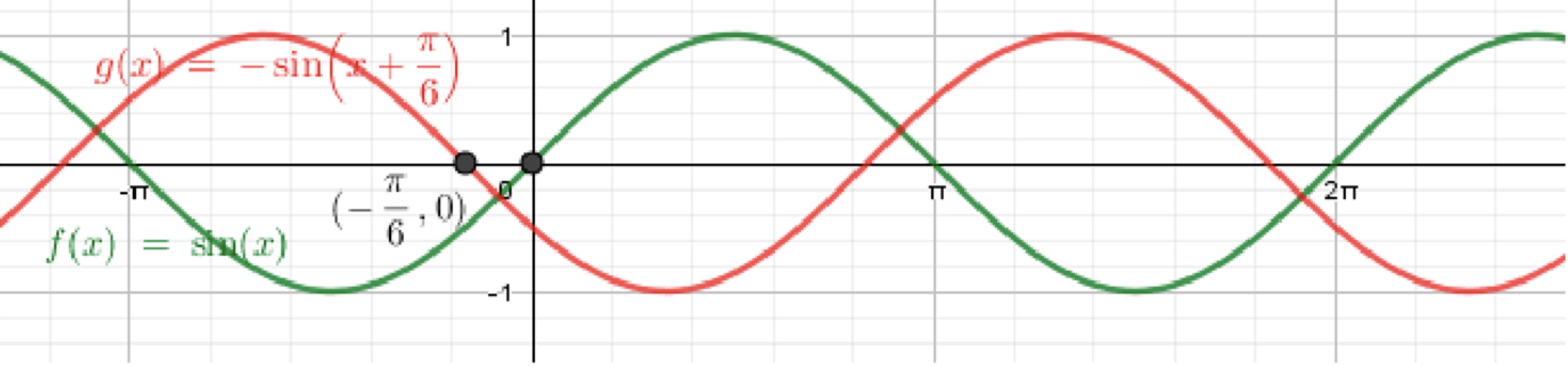
а) y = − sin ( x + π 6 ) y = -\sin \left( x + \frac{\pi}{6} \right)
Построим график функции y = sin x y = \sin x
Переместим его на π 6 \frac{\pi}{6}
Отразим его относительно оси абсцисс;
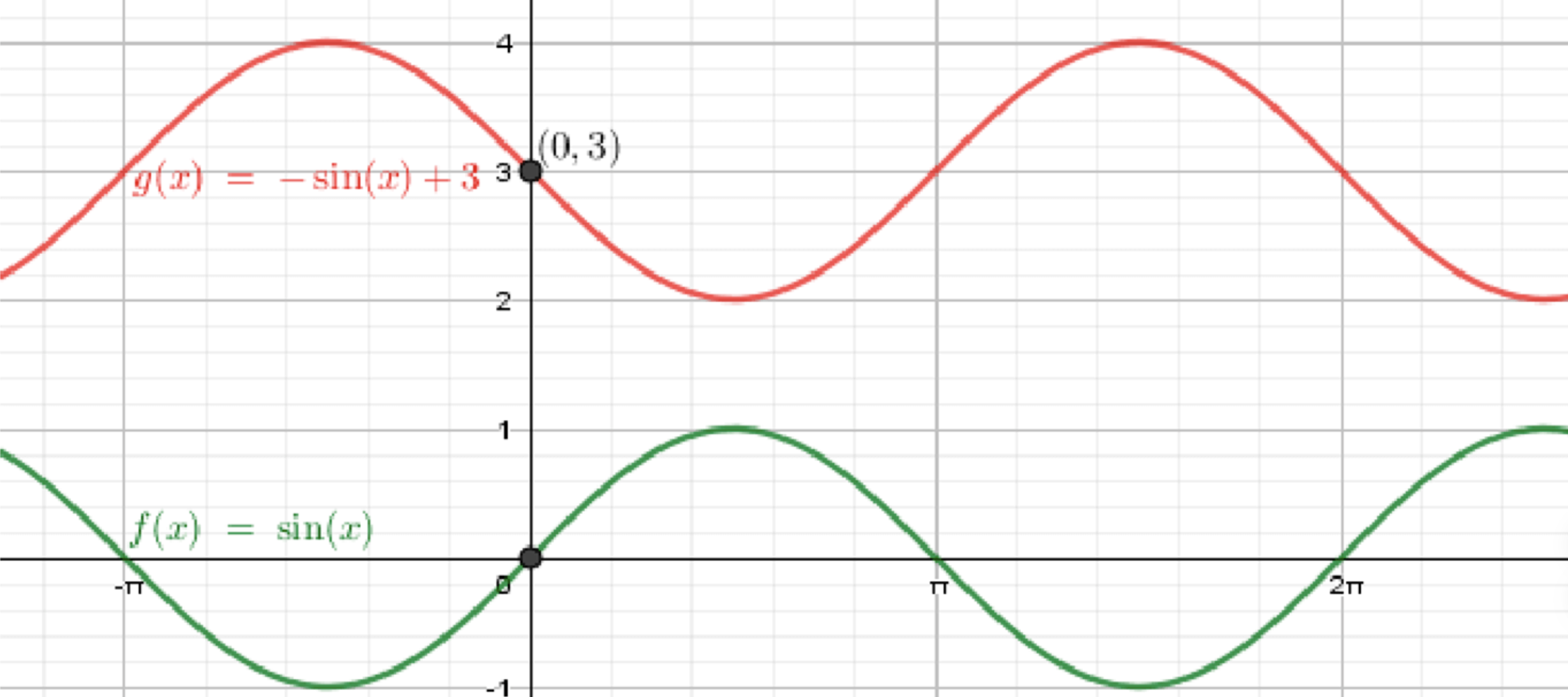
б) y = − sin x + 3 y = -\sin x + 3
Построим график функции y = sin x y = \sin x
Отразим его относительно оси абсцисс;
Переместим его на 3 единицы вверх;
Подробный ответ:
База преобразований
y = sin x y=\sin x 2 π 2\pi 1 1 y = 0 y=0 = 1 =1 x = π 2 + 2 π k x=\frac{\pi}{2}+2\pi k = − 1 =-1 x = 3 π 2 + 2 π k x=\frac{3\pi}{2}+2\pi k x = π k x=\pi k Горизонтальный сдвиг: sin ( x − a ) \sin(x-a) a a sin ( x + a ) \sin(x+a) a a Отражение относительно оси O x Ox y = − f ( x ) y=-f(x) Вертикальный сдвиг: y = f ( x ) + d y=f(x)+d d d y = d y=d [ d − 1 , d + 1 ] [d-1,d+1] а) y = − sin ( x + π 6 ) y=-\sin\!\Big(x+\tfrac{\pi}{6}\Big)
Параметры
Область определения: R \mathbb{R} Период: 2 π 2\pi Амплитуда: 1 1 Средняя линия: y = 0 y=0 Диапазон значений: [ − 1 , 1 ] [-1,1] Преобразования: сдвиг влево на π 6 \tfrac{\pi}{6} O x Ox Опорные точки (за один «шаблонный» ход)
Удобно взять точки, сдвинутые на − π 6 -\tfrac{\pi}{6}
x = π 6 − π 6 = 0 ⇒ y = − sin ( π 6 ) = − 1 2 , x = π 2 − π 6 = π 3 ⇒ y = − sin ( π 2 ) = − 1 ( минимум ) , x = π − π 6 = 5 π 6 ⇒ y = − sin ( π ) = 0 ( нуль/перегиб ) , x = 3 π 2 − π 6 = 4 π 3 ⇒ y = − sin ( 3 π 2 ) = 1 ( максимум ) , x = 2 π − π 6 = 11 π 6 ⇒ y = − sin ( 2 π ) = 0 ( нуль/перегиб ) . \begin{aligned} x&=\tfrac{\pi}{6} \!-\! \tfrac{\pi}{6}=0 \quad &&\Rightarrow\ y=-\sin\!\big(\tfrac{\pi}{6}\big)=-\tfrac12,\\ x&=\tfrac{\pi}{2} \!-\! \tfrac{\pi}{6}=\tfrac{\pi}{3} \quad &&\Rightarrow\ y=-\sin\!\big(\tfrac{\pi}{2}\big)=-1\ \ (\text{минимум}),\\ x&=\pi \!-\! \tfrac{\pi}{6}=\tfrac{5\pi}{6} \quad &&\Rightarrow\ y=-\sin(\pi)=0\ \ (\text{нуль/перегиб}),\\ x&=\tfrac{3\pi}{2} \!-\! \tfrac{\pi}{6}=\tfrac{4\pi}{3} \quad &&\Rightarrow\ y=-\sin\!\big(\tfrac{3\pi}{2}\big)=1\ \ (\text{максимум}),\\ x&=2\pi \!-\! \tfrac{\pi}{6}=\tfrac{11\pi}{6} \quad &&\Rightarrow\ y=-\sin(2\pi)=0\ \ (\text{нуль/перегиб}). \end{aligned}
Нули и экстремумы
Нули: sin ( x + π 6 ) = 0 ⇒ x + π 6 = π n ⇒ x = − π 6 + π n \sin(x+\tfrac{\pi}{6})=0 \Rightarrow x+\tfrac{\pi}{6}=\pi n \Rightarrow x=-\tfrac{\pi}{6}+\pi n [ 0 , 2 π ] [0,2\pi] x = 5 π 6 , 11 π 6 x=\tfrac{5\pi}{6},\ \tfrac{11\pi}{6} Максимумы: когда sin ( x + π 6 ) = − 1 ⇒ x + π 6 = 3 π 2 + 2 π k ⇒ x = 4 π 3 + 2 π k \sin(x+\tfrac{\pi}{6})=-1\Rightarrow x+\tfrac{\pi}{6}=\tfrac{3\pi}{2}+2\pi k\Rightarrow x=\tfrac{4\pi}{3}+2\pi k y = 1 y=1 Минимумы: когда sin ( x + π 6 ) = 1 ⇒ x + π 6 = π 2 + 2 π k ⇒ x = π 3 + 2 π k \sin(x+\tfrac{\pi}{6})=1\Rightarrow x+\tfrac{\pi}{6}=\tfrac{\pi}{2}+2\pi k\Rightarrow x=\tfrac{\pi}{3}+2\pi k y = − 1 y=-1 Монотонность (через производную y ′ = − cos ( x + π 6 ) y’=-\cos(x+\tfrac{\pi}{6})
Критические точки: cos ( x + π 6 ) = 0 ⇒ x = π 3 + π k \cos(x+\tfrac{\pi}{6})=0 \Rightarrow x=\tfrac{\pi}{3}+\pi k На [ 0 , 2 π ] [0,2\pi] ( 0 , π 3 ) (0,\tfrac{\pi}{3}) ( π 3 , 4 π 3 ) (\tfrac{\pi}{3},\tfrac{4\pi}{3}) ( 4 π 3 , 2 π ) (\tfrac{4\pi}{3},2\pi) Выпуклость (вторая производная y ′ ′ = sin ( x + π 6 ) y»=\sin(x+\tfrac{\pi}{6})
Вниз (вогнута вниз, y ′ ′ < 0 y»<0 ( 5 π 6 , 11 π 6 ) (\tfrac{5\pi}{6},\tfrac{11\pi}{6}) Вверх (выпукла вверх, y ′ ′ > 0 y»>0 ( 0 , 5 π 6 ) (0,\tfrac{5\pi}{6}) ( 11 π 6 , 2 π ) (\tfrac{11\pi}{6},2\pi) Точки перегиба: там, где y ′ ′ = 0 y»=0 x = − π 6 + π n x=-\tfrac{\pi}{6}+\pi n [ 0 , 2 π ] [0,2\pi] x = 5 π 6 , 11 π 6 x=\tfrac{5\pi}{6},\ \tfrac{11\pi}{6} y y Пересечения с осями
С O y Oy x = 0 ⇒ y = − sin ( π 6 ) = − 1 2 x=0\Rightarrow y=-\sin\!\big(\tfrac{\pi}{6}\big)=-\tfrac12 С O x Ox x = 5 π 6 , 11 π 6 x=\tfrac{5\pi}{6},\ \tfrac{11\pi}{6} Как построить (на бумаге)
Разметьте по x x 0 , π 3 , 5 π 6 , 4 π 3 , 11 π 6 , 2 π 0,\ \tfrac{\pi}{3},\ \tfrac{5\pi}{6},\ \tfrac{4\pi}{3},\ \tfrac{11\pi}{6},\ 2\pi Поставьте точки: ( 0 , − 1 2 ) (0,-\tfrac12) ( π 3 , − 1 ) (\tfrac{\pi}{3},-1) ( 5 π 6 , 0 ) (\tfrac{5\pi}{6},0) ( 4 π 3 , 1 ) (\tfrac{4\pi}{3},1) ( 11 π 6 , 0 ) (\tfrac{11\pi}{6},0) Соедините плавной синусоидой, следя за убыванием/возрастанием и выпуклостью на указанных интервалах. Продолжайте периодически с шагом 2 π 2\pi
б) y = − sin x + 3 y=-\sin x+3
Параметры
Область определения: R \mathbb{R} Период: 2 π 2\pi Амплитуда: 1 1 Средняя линия: y = 3 y=3 Диапазон значений: [ 2 , 4 ] [2,4] Преобразования: сначала отражение y = − sin x y=-\sin x вверх на 3 3 Опорные точки (за период [ 0 , 2 π ] [0,2\pi]
( 0 , 3 ) , ( π 2 , 2 ) (минимум) , ( π , 3 ) , ( 3 π 2 , 4 ) (максимум) , ( 2 π , 3 ) . (0,3),\quad \Big(\tfrac{\pi}{2},\,2\Big)\ \text{(минимум)},\quad (\pi,3),\quad \Big(\tfrac{3\pi}{2},\,4\Big)\ \text{(максимум)},\quad (2\pi,3).
Нули и экстремумы
Нули: − sin x + 3 = 0 ⇒ sin x = 3 -\sin x+3=0 \Rightarrow \sin x=3 нет решений (график не пересекает O x Ox Максимумы: x = 3 π 2 + 2 π k x=\tfrac{3\pi}{2}+2\pi k y = 4 y=4 Минимумы: x = π 2 + 2 π k x=\tfrac{\pi}{2}+2\pi k y = 2 y=2 Монотонность (производная y ′ = − cos x y’=-\cos x
Критические точки: cos x = 0 ⇒ x = π 2 + π k \cos x=0 \Rightarrow x=\tfrac{\pi}{2}+\pi k На [ 0 , 2 π ] [0,2\pi] ( 0 , π 2 ) (0,\tfrac{\pi}{2}) ( 3 π 2 , 2 π ) (\tfrac{3\pi}{2},2\pi) ( π 2 , 3 π 2 ) (\tfrac{\pi}{2},\tfrac{3\pi}{2}) Выпуклость (вторая производная y ′ ′ = sin x y»=\sin x
Вверх (y ′ ′ > 0 y»>0 ( 0 , π ) (0,\pi) Вниз (y ′ ′ < 0 y»<0 ( π , 2 π ) (\pi,2\pi) Точки перегиба: x = π k x=\pi k [ 0 , 2 π ] [0,2\pi] 0 , π , 2 π 0,\ \pi,\ 2\pi y = 3 y=3 Пересечения с осями
С O y Oy x = 0 ⇒ y = 3 x=0\Rightarrow y=3 С O x Ox [ 2 , 4 ] [2,4] выше оси O x Ox Как построить (на бумаге)
Проведите среднюю линию y = 3 y=3 y = 2 y=2 y = 4 y=4 Разметьте по x x 0 , π 2 , π , 3 π 2 , 2 π 0,\ \tfrac{\pi}{2},\ \pi,\ \tfrac{3\pi}{2},\ 2\pi Поставьте опорные точки и соедините плавной волной: вниз к минимуму ( π 2 , 2 ) (\tfrac{\pi}{2},2) ( π , 3 ) (\pi,3) ( 3 π 2 , 4 ) (\tfrac{3\pi}{2},4) ( 2 π , 3 ) (2\pi,3) Повторите периодически с шагом 2 π 2\pi