ГДЗ 10-11 Класс Номер 10.15 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции у = f(x), где:

а)

$$y = \begin{cases} x^2, & \text{если } x < 0; \\ \sin x, & \text{если } x \geq 0; \end{cases}$$

б)

$$y=\{\begin{array}{ll}\sin x,& \text{если }x<0\\ x^2,& \text{если }x\ge 0\end{array}$$

Построить график функции $y = f(x)$, где:

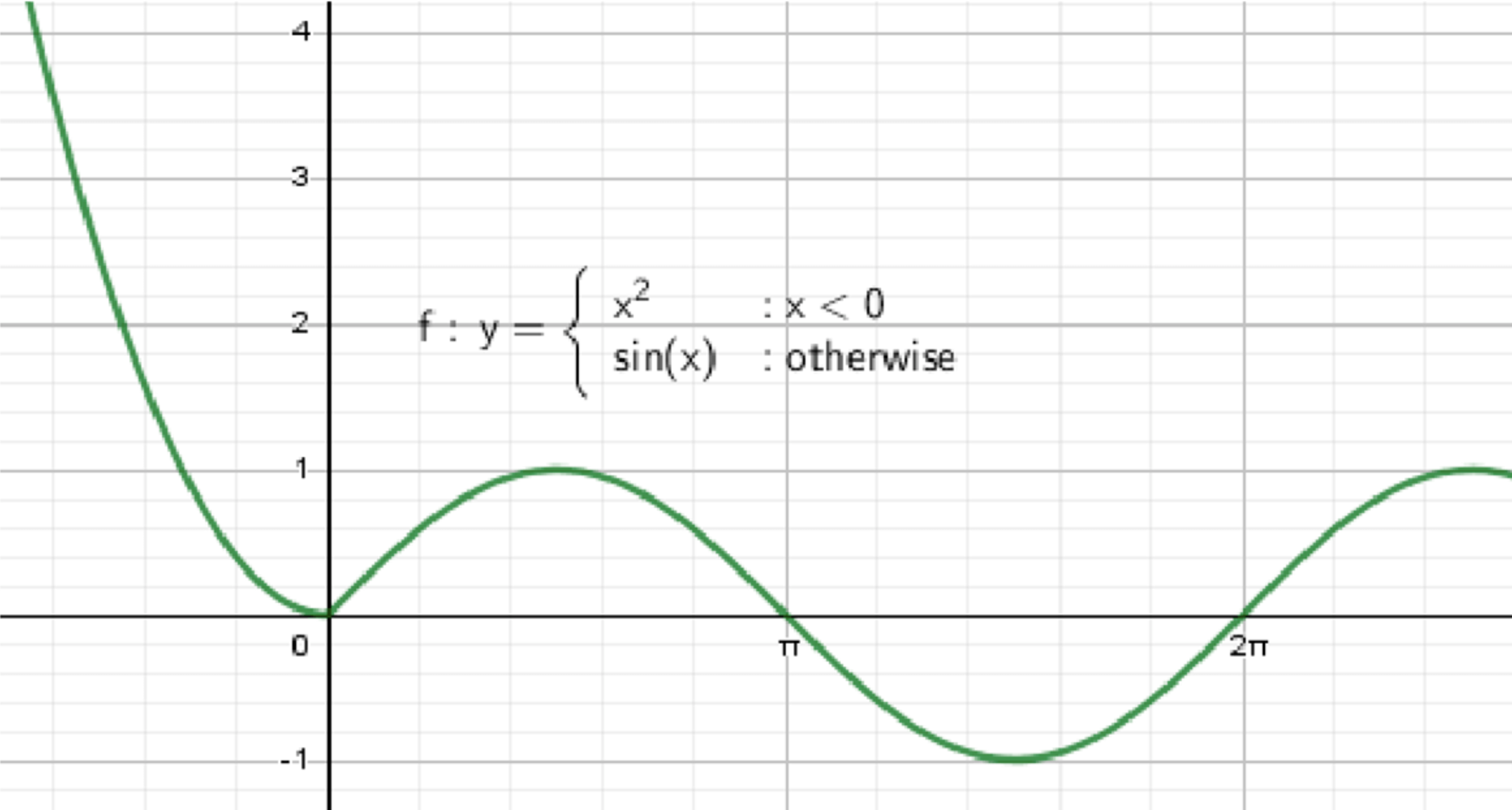
а)

$$y = \begin{cases} x^2, & \text{если } x < 0; \\ \sin x, & \text{если } x \geq 0; \end{cases}$$

$y = \sin x$ — уравнение синусоиды:
$y(0) = \sin 0 = 0$;

$y = x^2$ — уравнение параболы:
$x_0 = 0, \, y_0 = 0$;

График функции:

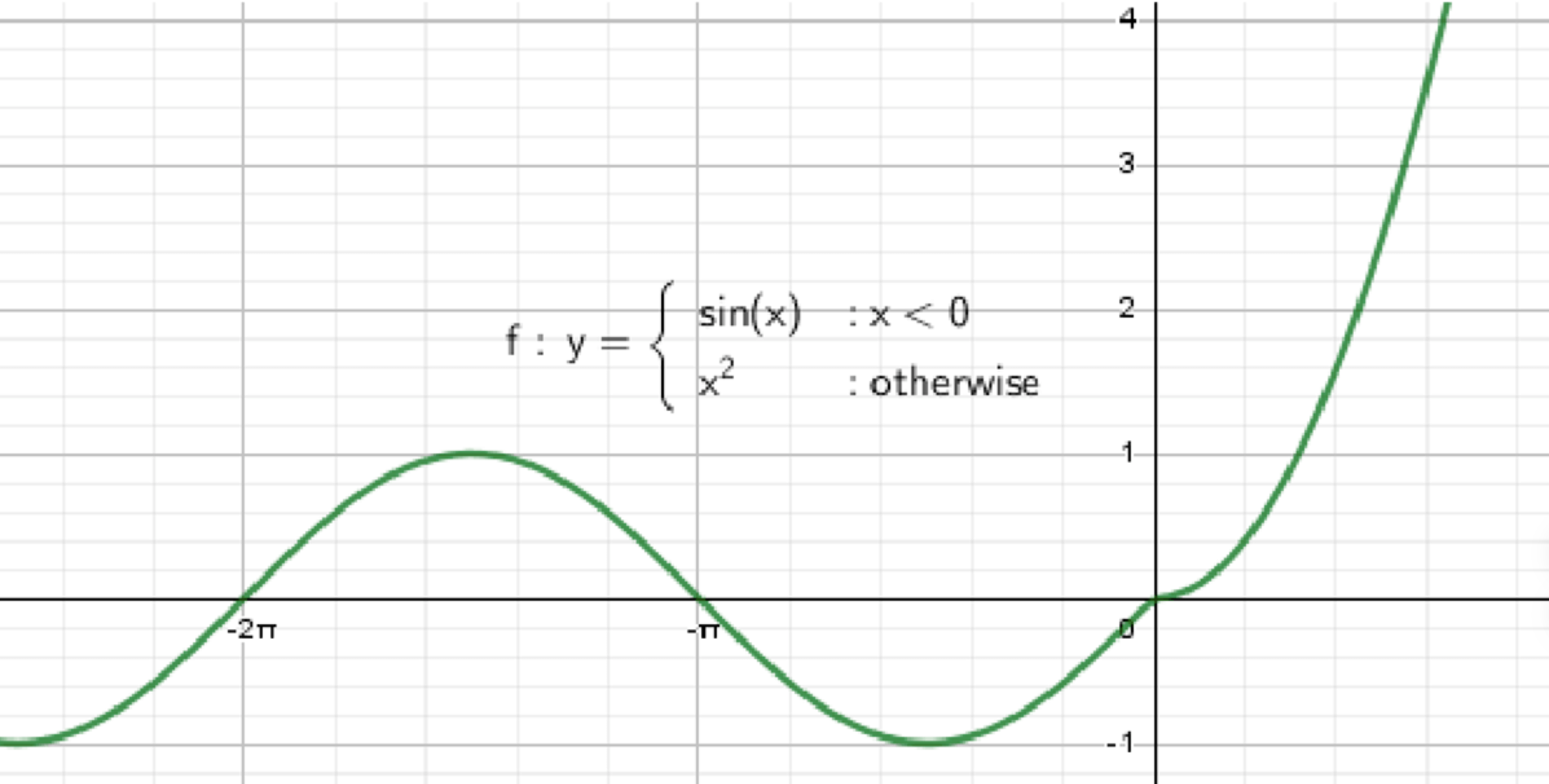
б)

$$y = \begin{cases} \sin x, & \text{если } x < 0; \\ x^2, & \text{если } x \geq 0; \end{cases}$$

$y = \sin x$ — уравнение синусоиды:
$y(0) = \sin 0 = 0$;

$y = x^2$ — уравнение параболы:
$x_0 = 0, \, y_0 = 0$;

График функции:

Построить график функции $y=f(x)$

a) $\; y=\begin{cases}x^2,& x<0\\ \sin x,& x\ge 0\end{cases}$

1) Область определения и значения

• Область определения: все $x\in\mathbb{R}$ (оба выражения заданы для всех $x$).
• Область значений:
  $\;x^2$ при $x<0$ даёт $y>0$ и стремится к $+\infty$ при $x\to-\infty$;
  $\;\sin x$ при $x\ge0$ даёт $[-1,1]$.
  Итого: $y\in[-1,+\infty)$.

2) Точки «склейки» и непрерывность

• Граница разбиения — $x=0$.
• Значение в точке: берём правую ветвь ($\sin x$): $f(0)=\sin0=0$.
• Левосторонний предел: $\lim_{x\to0^-}x^2=0$.
• Правосторонний предел: $\lim_{x\to0^+}\sin x=0$.
• Пределы равны значению ⇒ функция непрерывна в $x=0$ и, конечно, на каждом из промежутков.

3) Дифференцируемость в $x=0$

• Слева: $(x^2)’\!=2x\Rightarrow f’_-(0)=0$.
• Справа: $(\sin x)’\!=\cos x\Rightarrow f’_+(0)=1$.
• Односторонние производные не совпадают ⇒ в $x=0$ недифференцируема (излом).

4) Нули, знаки, экстремумы

• Нули: при $x<0$ $x^2>0$ ⇒ нулей нет; при $x\ge0$: $\sin x=0$ при $x=n\pi,\;n=0,1,2,\dots$.
  Значит, нули: $\{0,\pi,2\pi,3\pi,\dots\}$.
• Знак:
  • для $x<0$: $f(x)=x^2>0$;
  • для $x\ge0$: знак $\sin x$ (отрицателен на $(\pi,2\pi)+2\pi k$).
• Экстремумы: на $x<0$ ветвь $x^2$ монотонно убывает к 0; на $x\ge0$ экстремумы синуса: максимумы $=1$ в $x=\frac{\pi}{2}+2\pi k$, минимумы $=-1$ в $x=\frac{3\pi}{2}+2\pi k$ (для $k\ge0$).
  Глобальный минимум функции — $-1$ (достигается у синуса), глобального максимума нет (из-за роста $x^2$ слева к $+\infty$).

5) Монотонность и поведение на бесконечности

• На $(-\infty,0)$: убывает (потому что $x^2$ убывает при движении к 0 слева).
• На $[0,\infty)$: колеблется (синус).
• $x\to-\infty:\; f(x)\to+\infty$.
• $x\to+\infty:\; f(x)$ ограничена синусом в $[-1,1]$.

6) Как рисовать

1. На $x<0$ — левая ветвь параболы $y=x^2$, без точки в $x=0$ (открытый кружок).
2. В $x\ge0$ — синусоида, начиная с точки $(0,0)$ (закрытая точка).
3. Поставить характерные точки синуса: $0,\ \frac{\pi}{2},\ \pi,\ \frac{3\pi}{2},\ 2\pi,\dots$.
4. Провести оси/сетку — видно излом касания в $(0,0)$: касательная справа имеет наклон 1, слева — 0.

б) $\; y=\begin{cases}\sin x,& x<0\\ x^2,& x\ge 0\end{cases}$

1) Область определения и значения

• Область определения: $\mathbb{R}$.
• Область значений: $[-1,1]$ слева и $[0,+\infty)$ справа ⇒ снова $y\in[-1,+\infty)$.

2) Непрерывность в $x=0$

• Значение: берём правую ветвь $x^2$: $f(0)=0$.
• $\lim_{x\to0^-}\sin x=0$, $\lim_{x\to0^+}x^2=0$ ⇒ непрерывна в $0$.

3) Дифференцируемость в $x=0$

• Слева: $(\sin x)’\!=\cos x\Rightarrow f’_-(0)=1$.
• Справа: $(x^2)’\!=2x\Rightarrow f’_+(0)=0$.
• Производные разные ⇒ в $0$ недифференцируема (излом, но «наоборот», чем в пункте a).

4) Нули, знаки, экстремумы

• Нули: при $x\ge0$: $x^2=0\Rightarrow x=0$; при $x<0$: $\sin x=0$ при $x=n\pi,\; n=-1,-2,-3,\dots$.
  Итого нули: $\{0,-\pi,-2\pi,-3\pi,\dots\}$.
• Знак:
  • слева — знак $\sin x$ (например, отрицателен на $(-2\pi,-\pi)$, $(-\pi,0)$ меняет знак);
  • справа $x^2\ge0$.
• Экстремумы: слева — экстремумы синуса: макс $=1$ при $x=-\frac{3\pi}{2}+2\pi k$, мин $=-1$ при $x=-\frac{\pi}{2}+2\pi k$ (для отрицательных $x$); справа — у $x^2$ минимум в $x=0$, далее неограниченно возрастает.
  Глобальный минимум снова $-1$; глобального максимума нет (правая ветвь растёт).

5) Монотонность и поведение на бесконечности

• На $(-\infty,0)$: колеблется (синус).
• На $[0,\infty)$: монотонно возрастает (квадратичная).
• $x\to-\infty:$ ограниченные колебания в $[-1,1]$.
• $x\to+\infty:$ $f(x)\to+\infty$.

6) Как рисовать

1. На $x<0$ — синусоида, без точки в $x=0$ (открытый кружок).
2. На $x\ge0$ — правая половина параболы $y=x^2$ с точкой в $(0,0)$.
3. Отметить характерные узлы синуса слева: $-\frac{\pi}{2},-\pi,-\frac{3\pi}{2},-2\pi,\dots$.
4. Видно, что касательные по разные стороны имеют углы 1 и 0 соответственно — излом.