ГДЗ 10-11 Класс Номер 10.17 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

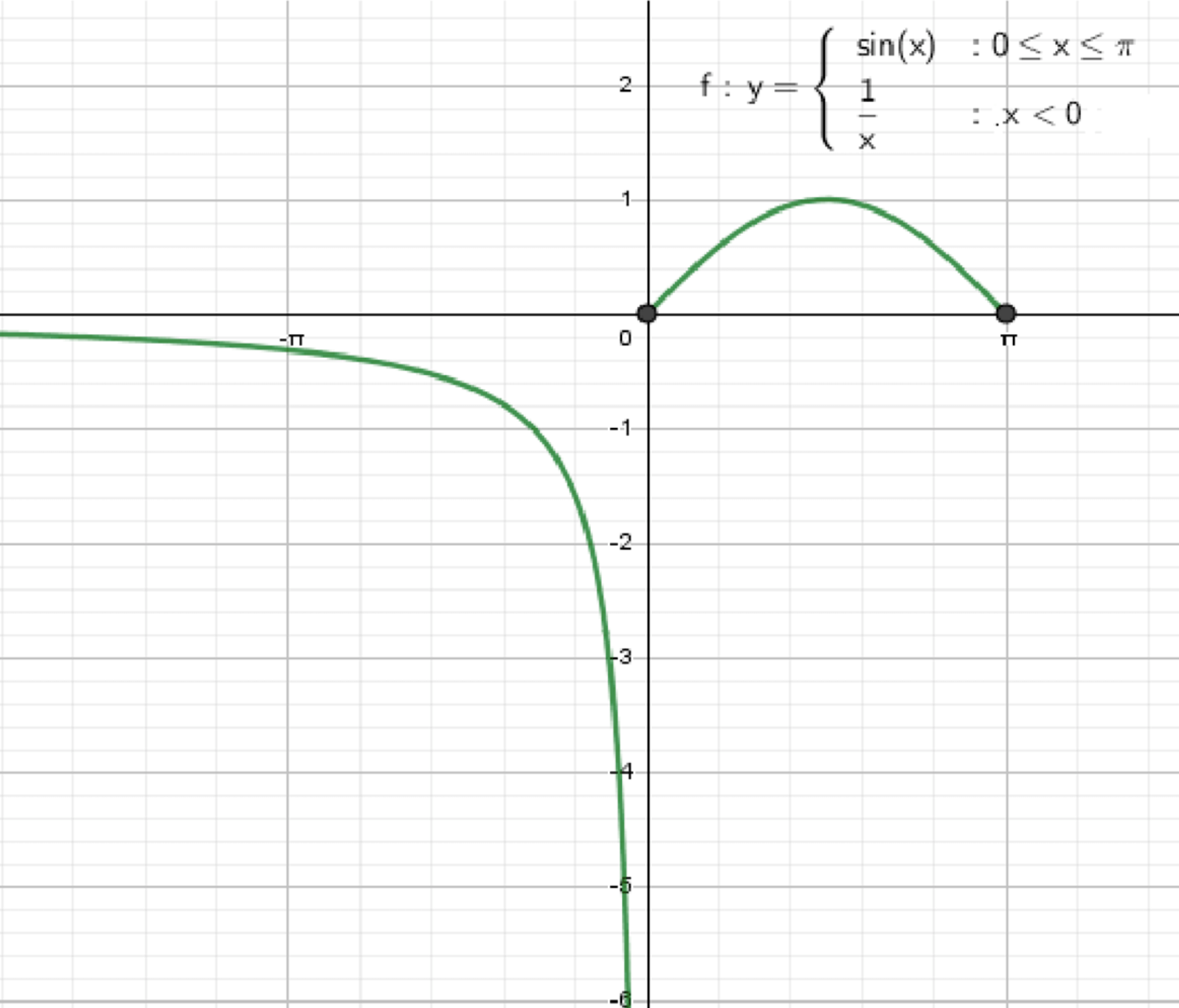
Дана функция $y=f(x)$, где

$$f(x)=\{\begin{array}{ll}\frac{1}{x},& \text{если }x<0,\\ \sin x,& \text{если }0\le x\le \pi \mathrm{.}\end{array}$$

а) Вычислите: $f(-2)$, $f(0)$, $f(1)$;

б) Постройте график функции $y=f(x)$;

в) Прочитайте график функции $y=f(x)$.

Дана функция: $f(x)=\{\begin{array}{l}\frac{1}{x},\text{ если }x<0\\ \sin x,\text{ если }0\le x\le \pi \end{array}$

а) Найдём значения:

$f(-2)=\frac{1}{-2}=-0,5;$

$f(0)=\sin 0=0;$

$f(1)=\sin 1;$

б) $y=\sin x$ — уравнение синусоиды:

$$\begin{array}{cccc}x& 0& \frac{\pi }{2}& \pi \\ y& 0& 1& 0\end{array}$$

$y=\frac{1}{x}$ — уравнение гиперболы:

$x_0=0,y_0=0;$

$$\begin{array}{cccc}x& -2& -1& -0,5\\ y& -0,5& -1& -2\end{array}$$

в) Свойства функции:

— $D(f)=(-\mathrm{\infty };\pi ];E(f)=(-\mathrm{\infty };1];$

— Возрастает на $[0;\frac{\pi }{2}];$

— Убывает на $(-\mathrm{\infty };0)\cup [\frac{\pi }{2};\pi ];$

— $f(x)>0$ на $(0;\pi );$

— $f(x)<0$ на $(-\mathrm{\infty };0);$

— Ограничена сверху;

— $y_{\max }=f\left(\frac{\pi }{2}\right)=1;$

— Ни чётная, ни нечётная;

— Не является периодической;

— Непрерывна на $(-\mathrm{\infty };0)\cup (0;\pi ].$

Условие

$$f(x)=\{\begin{array}{ll}{\displaystyle \frac{1}{x}},& x<0,\\ \sin x,& 0\le x\le \pi \mathrm{.}\end{array}$$

а) Точные значения

$x=-2<0\Rightarrow$ берём ветвь $1\mathrm{/}x$:

$$f(-2)=\frac{1}{-2}=-\frac{1}{2}=-\mathrm{0,5.}$$

$x=0\in [0,\pi ]\Rightarrow$ берём ветвь $\sin x$:

$$f(0)=\sin 0=0.$$

$x=1\in [0,\pi ]\Rightarrow$ опять $\sin x$:

$$f(1)=\sin 1(\text{численно }\approx \mathrm{0,84147})\mathrm{.}$$

б) Построение графика

Идея: рисуем две части и объединяем на одном поле координат.

Ветвь 1: $y={\displaystyle \frac{1}{x}},x<0$

• Область определения этой ветви: $(-\mathrm{\infty },0)$.
• Асимптоты: вертикальная $x=0$; горизонтальная $y=0$ при $x\to -\mathrm{\infty }$.
• Знак: на всём промежутке $y<0$.
• Монотонность: производная $y^{\mathrm{\prime }}=-1\mathrm{/}{x}^2<0\Rightarrow$ строго убывает на $(-\mathrm{\infty },0)$.
• Выпуклость: $y^{\mathrm{\prime }\mathrm{\prime }}=2\mathrm{/}{x}^3<0$ (так как $x<0$) ⇒ ветвь вогнута вниз.
• Опорные точки для эскиза: $(-2,-\mathrm{0,5}),(-1,-1),(-\mathrm{0,5},-2)$.

Ветвь 2: $y=\sin x,0\le x\le \pi$

• Область определения ветви: $[0,\pi ]$.
• Опорные точки: $(0,0),(\frac{\pi }{2},1),(\pi ,0)$.
• Монотонность: $\sin x$ возрастает на $[0,\frac{\pi }{2}]$ (так как $\cos x\ge 0$) и убывает на $[\frac{\pi }{2},\pi ]$ (так как $\cos x\le 0$).
• Экстремум: максимум $y_{\max }=1$ при $x=\frac{\pi }{2}$.
• Знак: на $(0,\pi )$ положительна, в концах $x=0,\pi$ равна нулю.
• Выпуклость: $y^{\mathrm{\prime }\mathrm{\prime }}=-\sin x\le 0$ на $[0,\pi ]$ ⇒ вогнута вниз (внутри интервала строго).

Как совместить

• Точка $x=0$ принадлежит правой ветви: на графике есть закрашенная точка $(0,0)$.
• Слева от нуля ветвь гиперболы стремится к $-\mathrm{\infty }$ при $x\to 0^{-}$, то есть в $x=0$ разрыв по типу вертикальной асимптоты для левой части.
• В остальном просто рисуем обе части на одной системе координат.

в) «Прочитать» (проанализировать) график функции

Область определения (где задана):

$$D(f)=(-\mathrm{\infty },0)\cup [0,\pi ]=(-\mathrm{\infty },\pi ]\mathrm{.}$$

Множество значений (что принимает):

• для $x<0$: $1\mathrm{/}x<0\Rightarrow (-\mathrm{\infty },0)$;
• для $0\le x\le \pi$: $\sin x\in [0,1]$.
  Итого:

$$E(f)=(-\mathrm{\infty },1]\mathrm{.}$$

Нули функции (где $f(x)=0$):

$$x=0,x=\pi \mathrm{.}$$

Знак функции:

$$f(x)<0\text{ на }(-\mathrm{\infty },0),f(x)>0\text{ на }(0,\pi )\mathrm{.}$$

Монотонность:

$$\begin{array}{rl}{\displaystyle }& {\displaystyle \text{убывает на }(-\mathrm{\infty },0)(\text{ветвь }1\mathrm{/}x),}\\ {\displaystyle }& {\displaystyle \text{возрастает на }[0,\frac{\pi }{2}],}\\ {\displaystyle }& {\displaystyle \text{убывает на }[\frac{\pi }{2},\pi ]\mathrm{.}}\end{array}$$

Экстремумы:
Единственный максимум на отрезке $[0,\pi ]$:

$$x=\frac{\pi }{2},f\text{\hspace{0.17em}⁣}\left(\frac{\pi }{2}\right)=1.$$

Минимумов нет (слева значения уходят к $-\mathrm{\infty }$).

Ограниченность:
Сверху ограничена числом $1$; снизу не ограничена (значения уходят к $-\mathrm{\infty }$ при $x\to 0^{-}$).

Непрерывность:

$$\text{непрерывна на }(-\mathrm{\infty },0)\cup (0,\pi ],\text{ в точке }x=0\text{— разрыв }$$

Дифференцируемость:
Дифференцируема на $(-\mathrm{\infty },0)\cup (0,\pi )$. В $x=0$ не дифференцируема (из-за разрыва).

Асимптоты:
Для левой ветви $y=\frac{1}{x}$: вертикальная $x=0$ и горизонтальная $y=0$ (при $x\to -\mathrm{\infty }$).

Чётность/нечётность:
Функция не чётная и не нечётная (из-за кусочной заданности и разных областей).

Периодичность:
Не периодическая (часть $\sin x$ ограничена отрезком, а другая часть — не периодична).

Пересечения с осями:

• с осью $Ox$: точки $(0,0)$ и $(\pi ,0)$;
• с осью $Oy$: точка $(0,0)$.

Выпуклость:

• на $(-\mathrm{\infty },0)$ $f^{\mathrm{\prime }\mathrm{\prime }}(x)=2\mathrm{/}{x}^3<0\Rightarrow$ вогнута вниз;
• на $(0,\pi )$ $f^{\mathrm{\prime }\mathrm{\prime }}(x)=-\sin x<0\Rightarrow$ также вогнута вниз.