ГДЗ 10-11 Класс Номер 10.18 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x)=\{\begin{array}{ll}2x+2\pi ,& \text{если }x\le -\pi \\ \sin x,& \text{если }-\pi <x\le 0\\ -2x,& \text{если }x>0\end{array}$$

а) Вычислите: $$f(-\pi -2)$$$$f(-\pi — 2) = 2(-\pi — 2) + 2\pi = -4;$$ $$f(-\frac{\pi }{6})$$$$f\left(-\frac{\pi}{6}\right) = \sin\left(-\frac{\pi}{6}\right) = -\sin\frac{\pi}{6} = -0.5;$$ $$f(2)$$

б) Постройте график функции $y = f(x)$;

в) Прочитайте график функции $y = f(x)$.

Дана функция:

$$f(x) = \begin{cases} 2x + 2\pi, & \text{если } x \leq -\pi \\ \sin x, & \text{если } -\pi < x \leq 0 \\ -2x, & \text{если } x > 0 \end{cases}$$

а) Найдем значения:

$$f(-\pi — 2) = 2(-\pi — 2) + 2\pi = -4;$$ $$f\left(-\frac{\pi}{6}\right) = \sin\left(-\frac{\pi}{6}\right) = -\sin\frac{\pi}{6} = -0.5;$$ $$f(2) = -2 \cdot 2 = -4;$$

б) $y = 2x + 2\pi$ — уравнение прямой:

$y = \sin x$ — уравнение синусоиды:

$y = -2x$ — уравнение прямой:

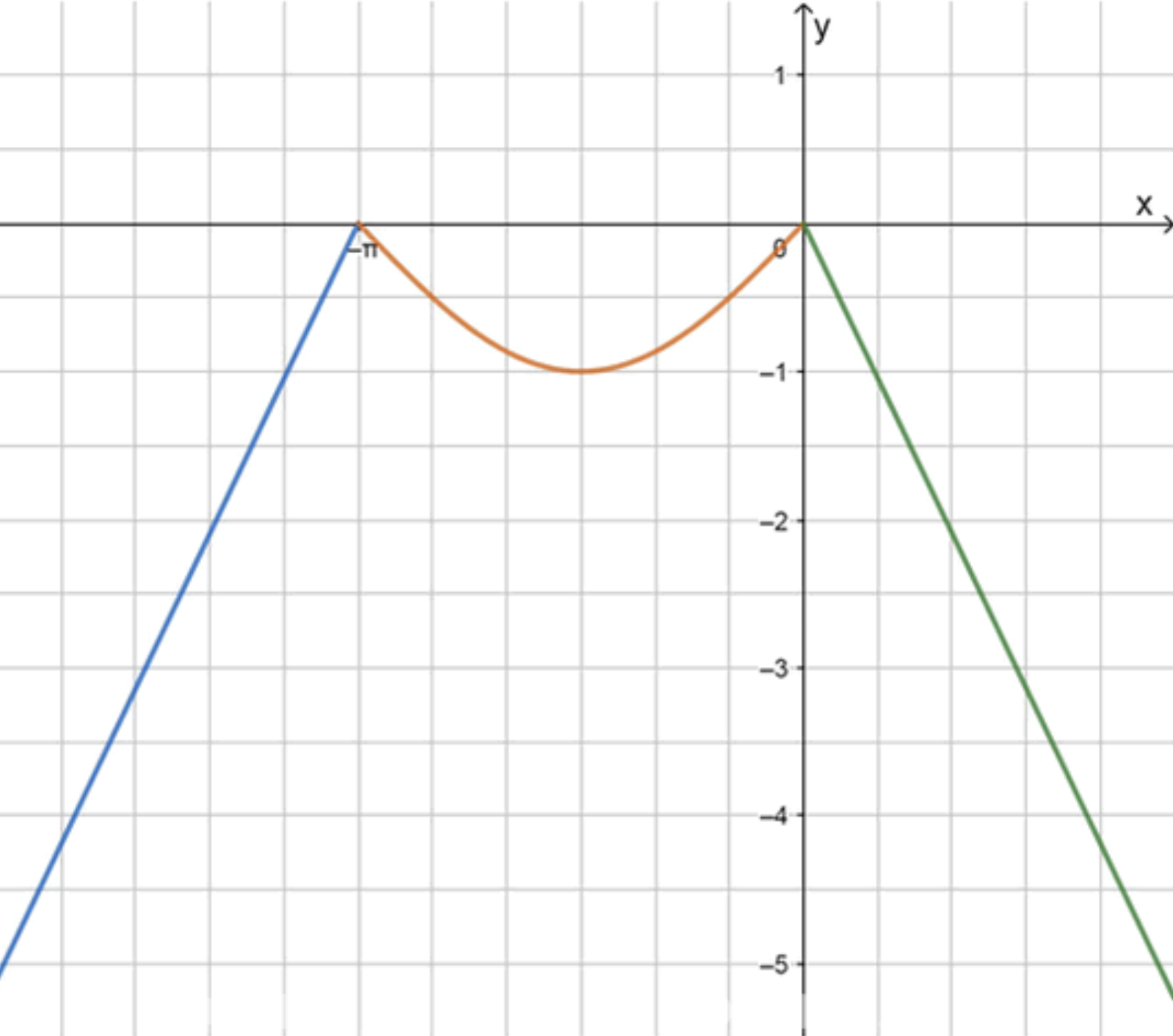
График функции:

в) Свойства функции:

• $D(f) = (-\infty; +\infty); E(f) = (-\infty; 0];$
• Возрастает на $(-\infty; -\pi] \cup \left[-\frac{\pi}{2}; 0\right];$
• Убывает на $\left[-\pi; -\frac{\pi}{2}\right] \cup [0; +\infty);$
• $f(x) < 0$ на $(-\infty; -\pi) \cup (-\pi; 0) \cup (0; +\infty);$
• Ограничена сверху;
• $y_{\max} = y(-\pi) = y(0) = 0;$
• Ни четная, ни нечетная;
• Не является периодической;
• Непрерывна на $(-\infty; +\infty);$

Дана кусочно-заданная функция

$$f(x)= \begin{cases} 2x+2\pi, & x\le -\pi,\\[4pt] \sin x, & -\pi<x\le 0,\\[4pt] -2x, & x>0. \end{cases}$$

а) Точные вычисления значений

$f(-\pi-2)$. Здесь $x\le -\pi$, значит берём первую ветвь:

$$f(-\pi-2)=2(-\pi-2)+2\pi=-2\pi-4+2\pi=-4.$$

$f\!\left(-\dfrac{\pi}{6}\right)$. Здесь $-\pi<-\dfrac{\pi}{6}\le 0$, берём вторую ветвь:

$$f\!\left(-\frac{\pi}{6}\right)=\sin\!\left(-\frac{\pi}{6}\right)=-\sin\!\left(\frac{\pi}{6}\right)=-\frac12=-0.5.$$

$f(2)$. Здесь $x>0$, берём третью ветвь:

$$f(2)=-2\cdot 2=-4.$$

б) Опорные точки для графика

Ветвь 1: $y=2x+2\pi$ при $x\le -\pi$

• При $x=-\pi$: $y=2(-\pi)+2\pi=0$.
• Возьмём ещё, скажем, $x=-\dfrac{4\pi}{3}$:

$$y=2\!\left(-\frac{4\pi}{3}\right)+2\pi=-\frac{8\pi}{3}+\frac{6\pi}{3}=-\frac{2\pi}{3}\approx-2.094\ (\text{в таблице округлено до }\approx-2).$$

Таблица:

$$\begin{array}{c|cc} x & -\dfrac{4\pi}{3} & -\pi\\ \hline y & \approx-2 & 0 \end{array}$$

Ветвь 2: $y=\sin x$ при $-\pi<x\le 0$

Ключевые точки на отрезке $[-\pi,0]$:

$$\begin{array}{c|ccc} x & -\pi & -\dfrac{\pi}{2} & 0\\\hline y & 0 & -1 & 0 \end{array}$$

Замечание: в формуле ветви точка $x=-\pi$ исключена, но предельное значение справа равно $0$; сама точка $x=-\pi$ принадлежит первой ветви и там $y=0$.

Ветвь 3: $y=-2x$ при $x>0$

$$\begin{array}{c|cc} x & 0 & 1\\ \hline y & 0 & -2 \end{array}$$

Замечание: $x=0$ относится к средней ветви, где $y=\sin 0=0$; у правой ветви при $x\to 0^+$ тоже предел $0$.

в) Свойства функции (с полными обоснованиями)

1) Область определения

Каждый из трёх кусочков покрывает свою часть: $(-\infty,-\pi]$, $(-\pi,0]$, $(0,+\infty)$. Их объединение — вся прямая:

$$D(f)=(-\infty,+\infty).$$

2) Непрерывность на всей прямой

Проверим точки склейки.

• В $x=-\pi$:
  Левая ветвь даёт $f(-\pi)=2(-\pi)+2\pi=0$.
  Правая по отношению к $-\pi$ (средняя ветвь) имеет правый предел $\lim\limits_{x\to-\pi+}\sin x=\sin(-\pi)=0$.
  Совпадает и значение, и пределы ⇒ непрерывно в $-\pi$.
• В $x=0$:
  Средняя ветвь даёт $f(0)=\sin 0=0$.
  Справа $\lim\limits_{x\to 0+}(-2x)=0$, слева $\lim\limits_{x\to 0-}\sin x=0$.
  Совпадает ⇒ непрерывно в $0$.

На внутренних точках каждого куска — стандартные непрерывные функции (линейные и $\sin x$).
Итог: $f$ непрерывна на $(-\infty,+\infty)$.

3) Дифференцируемость

Внутри кусков:

$$f'(x)= \begin{cases} 2,& x<-\pi,\\ \cos x,& -\pi<x<0,\\ -2,& x>0. \end{cases}$$

В точках склейки сравним односторонние производные:

• В $x=-\pi$: $f’_-( -\pi)=2$, $f’_+( -\pi)=\cos(-\pi)=-1$ ⇒ различны ⇒ не дифференцируема в $-\pi$.
• В $x=0$: $f’_-(0)=\cos 0=1$, $f’_+(0)=-2$ ⇒ различны ⇒ не дифференцируема в $0$.

Итак: $f$ непрерывна везде, но не дифференцируема в $x=-\pi$ и $x=0$.

4) Область значений

Рассмотрим каждую ветвь:

• $x\le -\pi$: $y=2x+2\pi$ — строг. возрастающая прямая.
  При $x=-\pi$ имеем $y=0$; при $x\to-\infty$, $y\to-\infty$.
  Диапазон ветви: $(-\infty,\,0]$.
• $-\pi<x\le 0$: $y=\sin x\in[-1,0]$ (на этом отрезке синус не положителен).
  Концы: при $x\to-\pi+$ предел $0$ (сама точка $-\pi$ у этой ветви не берётся), при $x=0$ — $0$, минимум $-1$ при $x=-\dfrac{\pi}{2}$.
• $x>0$: $y=-2x<0$, при $x\to 0^+$ $y\to 0$, при $x\to+\infty$ $y\to-\infty$.
  Диапазон ветви: $(-\infty,\,0)$.

Объединяя, получаем

$$E(f)=(-\infty,\,0].$$

5) Знаки, нули

Из только что найденного:

• $f(x)\le 0$ для всех $x$.
• Равенство $f(x)=0$ достигается в точках $x=-\pi$ (первая ветвь) и $x=0$ (вторая ветвь).
  На остальных $x$ — строго отрицательна:

$$f(x)<0\quad \text{при } x\in(-\infty,-\pi)\cup(-\pi,0)\cup(0,+\infty).$$

6) Монотонность (строго)

• На $(-\infty,-\pi]$: $y=2x+2\pi$ с угловым коэффициентом $2>0$ ⇒ строго возрастает.
• На $[-\pi,-\tfrac{\pi}{2}]$: $\sin x$ убывает (так как $\cos x\le 0$ на $[\tfrac{\pi}{2},\tfrac{3\pi}{2}]$, что соответствует $x\in[-\pi,0]$; конкретно от $-\pi$ до $-\tfrac{\pi}{2}$ — убывание от $0$ до $-1$).
• На $[-\tfrac{\pi}{2},0]$: $\sin x$ возрастает (от $-1$ до $0$).
• На $(0,+\infty)$: $y=-2x$ с угловым коэффициентом $-2<0$ ⇒ строго убывает.

Кратко:

$$\text{возрастает на }(-\mathrm{\infty },-\pi ]\cup [-\frac{\pi }{2},0],$$

$$\text{возрастает на }(-\infty,-\pi]\ \cup\ \left[-\frac{\pi}{2},0\right],\quad \text{убывает на }\left[-\pi,-\frac{\pi}{2}\right]\ \cup\ (0,+\infty).$$

7) Экстремумы

• На первой ветви экстремумов нет (строго возрастает), но правая граница $x=-\pi$ даёт наибольшее значение внутри этой ветви: $0$.
• На средней ветви $\sin x$ имеет минимум $-1$ в $x=-\dfrac{\pi}{2}$ (локальный и глобальный на этом куске); максимумы на границах: $0$ при $x=0$ (включена) и $0$ при $x\to -\pi+$ (сама точка $-\pi$ для этой ветви исключена).
• На правой ветви экстремумов нет (строго убывает).

Глобальные выводы:

• Глобальный максимум по всей $\mathbb{R}$: $y_{\max}=0$, достигается в двух точках $x=-\pi$ и $x=0$.
• Глобального минимума нет (функция не ограничена снизу: $f(x)\to-\infty$ при $x\to\pm\infty$ по своим линейным ветвям).
• Локальный минимум в $x=-\dfrac{\pi}{2}$: $f=-1$.

8) Ограниченность

• Сверху функция ограничена: $f(x)\le 0$ для всех $x$.
• Снизу не ограничена: при $x\to\pm\infty$ $f(x)\to-\infty$.
  Итог: «ограничена сверху», «не ограничена снизу».

9) Чётность/нечётность

Проверка на чётность требует $f(-x)=f(x)$ для всех $x$, на нечётность — $f(-x)=-f(x)$.
Из-за разных формул на разных полуосях равенства нарушаются (например, возьмём $x=1$: $f(1)=-2$, а $f(-1)=\sin(-1)\approx-0.84\neq\pm(-2)$).
Вывод: ни чётная, ни нечётная.

10) Периодичность

Если бы функция была периодической, все три кусочка должны были «повторяться» с одним периодом $T>0$. Но линейные куски на концах и синусоидальный в середине не могут согласованно повторяться одним и тем же периодом на всей $\mathbb{R}$.
Вывод: не является периодической.

11) Асипмтотика и поведение на бесконечности

• При $x\to -\infty$: $f(x)=2x+2\pi\to-\infty$ (линейная «левая» ветвь).
• При $x\to +\infty$: $f(x)=-2x\to-\infty$ (линейная «правая» ветвь).
  Горизонтальных асимптот нет; фактически «на хвостах» функция совпадает с прямыми своих линейных ветвей.

12) Пересечения с осями

• С осью $Oy$: в $x=0\Rightarrow f(0)=0$ ⇒ точка $(0,0)$.
• С осью $Ox$ (нули): $x=-\pi$ и $x=0$. Оба нуля простые (смены знака нет — функция не становится положительной, но переходит через 0 с «горизонтальным касанием» у синуса и с «ломаным сочленением» в $-\pi$).