ГДЗ 10-11 Класс Номер 10.19 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x)=\{\begin{array}{ll}-x^2,& \text{если }x<0\\ \sin x,& \text{если }0\le x\le \pi \\ -(x-\pi {)}^2,& \text{если }x>\pi \end{array}$$

а) Вычислите:

$$f(-3) = (-3)^2 = -9;$$ $$f\left(\frac{\pi}{2}\right) = \sin \frac{\pi}{2} = 1;$$ $$f(2\pi -3)$$

б) Постройте график функции $y = f(x)$;

в) Прочитайте график функции $y = f(x)$.

Дана функция:

$$f(x) = \begin{cases} -x^2, & \text{если } x < 0 \\ \sin x, & \text{если } 0 \leq x \leq \pi \\ -(x — \pi)^2, & \text{если } x > \pi \end{cases}$$

а) Найдем значения:

$$f(-3) = (-3)^2 = -9;$$ $$f\left(\frac{\pi}{2}\right) = \sin \frac{\pi}{2} = 1;$$ $$f(2\pi — 3) = -(2\pi — 3 — \pi)^2 = -(\pi — 3)^2;$$

б)

• $y = -x^2$ — уравнение параболы:

  $$x_0 = 0, \quad y_0 = 0;$$ $$\begin{array}{c|c c c} x & -2 & -1 & 0 \\ \hline y & -4 & -1 & 0 \\ \end{array}$$

• $y = \sin x$ — уравнение синусоиды:

  $$\begin{array}{c|c c c} x & 0 & \frac{\pi}{2} & \pi \\ \hline y & 0 & 1 & 0 \\ \end{array}$$

• $y = -(x — \pi)^2$ — уравнение параболы:

  $$x_0 = \pi, \quad y_0 = 0;$$ $$\begin{array}{c|c c c} x & \pi & \frac{4\pi}{3} & \frac{3\pi}{2} \\ \hline y & 0 & \approx -1 & \approx -2.5 \\ \end{array}$$

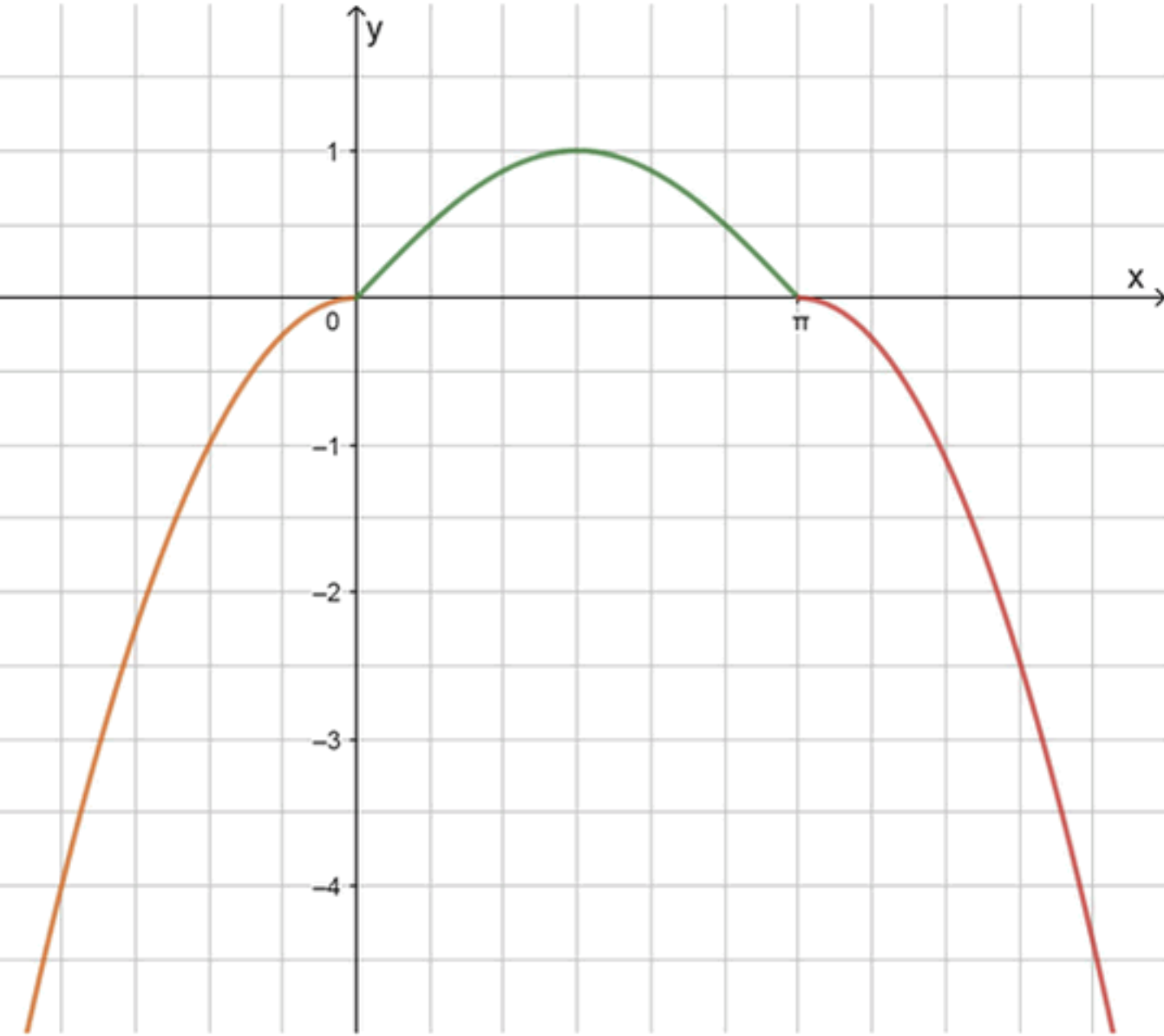
График функции:

в) Свойства функции:

• $D(f) = (-\infty; +\infty); \quad E(f) = (-\infty; 1];$
• Возрастает на $\left(-\infty; \frac{\pi}{2}\right];$
• Убывает на $\left[\frac{\pi}{2}; +\infty\right);$
• $f(x) > 0$ на $(0; \pi);$
• $f(x) < 0$ на $(-\infty; 0) \cup (\pi; +\infty);$
• Ограничена сверху;
• $y_{\max} = y\left(\frac{\pi}{2}\right) = 1;$
• Ни четная, ни нечетная;
• Не является периодической;
• Непрерывна на $(-\infty; +\infty);$

Определение

$$f(x)= \begin{cases} -x^2,& x<0,\\[2pt] \sin x,& 0\le x\le \pi,\\[2pt] -(x-\pi)^2,& x>\pi. \end{cases}$$

а) точные и численные значения

• $x=-3<0\Rightarrow f(-3)=-(-3)^2=-9$.
• $x=\dfrac{\pi}{2}\in[0,\pi]\Rightarrow f\!\left(\dfrac{\pi}{2}\right)=\sin\!\left(\dfrac{\pi}{2}\right)=1$.
• $x=2\pi-3>\pi\Rightarrow f(2\pi-3)=-(2\pi-3-\pi)^2=-(\pi-3)^2$.
  Численно: $\pi-3\approx 0.14159265$, $(\pi-3)^2\approx 0.02004848$, значит

$$f(2\pi-3)\approx -0.02004848\;.$$

б) Построение графика (как чертить вручную)

• Ветвь $x<0$: парабола $y=-x^2$, вершина в $(0,0)$, открыта вниз. Опорные точки: $(-2,-4)$, $(-1,-1)$, $(0,0)$.
• Участок $0\le x\le\pi$: синусоида от $0$ до $\pi$: $(0,0)\to(\tfrac{\pi}{2},1)\to(\pi,0)$.
• Ветвь $x>\pi$: парабола $y=-(x-\pi)^2$, вершина в $(\pi,0)$, открыта вниз. Опорные точки:
  $x=\tfrac{4\pi}{3}\Rightarrow y=-(\tfrac{\pi}{3})^2\approx-1.0966$;
  $x=\tfrac{3\pi}{2}\Rightarrow y=-(\tfrac{\pi}{2})^2\approx-2.4674$.

График непрерывно «склеивается» в узлах $x=0$ и $x=\pi$ (об этом ниже).

в)

1) Область определения и значения

Область определения. Все три формулы заданы на своих промежутках, а промежутки покрывают всю $\mathbb R$, значит

$$D(f)=(-\infty,+\infty).$$

Область значений.

• Для $x<0$: $y=-x^2\le 0$, причём $\lim_{x\to-\infty}(-x^2)=-\infty$.
• Для $0\le x\le\pi$: $\sin x\in[0,1]$, максимум $1$ при $x=\tfrac{\pi}{2}$, минимум $0$ при $x=0,\pi$.
• Для $x>\pi$: $y=-(x-\pi)^2\le 0$, и $\lim_{x\to+\infty}-(x-\pi)^2=-\infty$.

Итак, сверху $f$ ограничена числом $1$, достигаемым в $x=\tfrac{\pi}{2}$; снизу не ограничена:

$$E(f)=(-\infty,\,1].$$

2) Непрерывность

Каждая ветвь непрерывна на своём интервале. Проверим узлы.

• При $x=0$: $\lim\limits_{x\to0-}(-x^2)=0$, $\lim\limits_{x\to0+}\sin x=\sin0=0$, и $f(0)=\sin0=0$. Значит, непрерывна в $0$.
• При $x=\pi$: $\lim\limits_{x\to\pi-}\sin x=\sin\pi=0$, $\lim\limits_{x\to\pi+}-(x-\pi)^2=0$, и $f(\pi)=\sin\pi=0$. Значит, непрерывна в $\pi$.

Итог: $f$ непрерывна на всей $\mathbb R$.

3) Производная, монотонность, экстремумы

Производные по частям:

$$f'(x)= \begin{cases} -2x,& x<0,\\[2pt] \cos x,& 0<x<\pi,\\[2pt] -2(x-\pi),& x>\pi. \end{cases}$$

Односторонние производные в узлах:

$$f’_-(0)=\lim_{x\to0-}(-2x)=0,\qquad f’_+(0)=\cos0=1\quad(\text{не совпадают}),$$ $$f’_-(\pi)=\cos\pi=-1,\qquad f’_+(\pi)=\lim_{x\to\pi+}-2(x-\pi)=0\quad(\text{не совпадают}).$$

Значит, не дифференцируема в $x=0$ и $x=\pi$ (острые точки), но дифференцируема всюду иначе.

Знаки производной ⇒ монотонность.

• На $(-\infty,0)$: $f'(x)=-2x>0$ (так как $x<0$) ⇒ $f$ строго возрастает.
• На $(0,\tfrac{\pi}{2})$: $\cos x>0$ ⇒ строго возрастает.
• На $(\tfrac{\pi}{2},\pi)$: $\cos x<0$ ⇒ строго убывает.
• На $(\pi,+\infty)$: $-2(x-\pi)<0$ ⇒ строго убывает.

Склеивая интервалы и учитывая непрерывность в узлах $0$ и $\pi$, получаем:

$$\boxed{\text{возрастает на }(-\infty,\tfrac{\pi}{2}]},\qquad \boxed{\text{убывает на }[\tfrac{\pi}{2},+\infty)}.$$

Экстремумы. Единственная критическая точка внутри средней ветви — $x=\tfrac{\pi}{2}$, где $\cos x=0$. Там

$$f\!\left(\tfrac{\pi}{2}\right)=1\quad\text{— глобальный максимум (и локальный).}$$

Глобального минимума нет (функция уходит к $-\infty$ слева и справа).

4) Нули и знаки

• $f(x)=0$ в точках $x=0$ и $x=\pi$ (по определению и по непрерывности в узлах). Других нулей нет: на $(0,\pi)$ $\sin x>0$, а на $x<0$ и $x>\pi$ параболы строго отрицательны.
• Знак:

  $$f(x)>0\ \text{на }(0,\pi),\qquad f(x)<0\ \text{на }(-\infty,0)\cup(\pi,+\infty).$$

5) Ограниченность и предельное поведение

• Ограничена сверху числом $1$, достигаемым в $x=\tfrac{\pi}{2}$.
• Не ограничена снизу: $\lim\limits_{x\to\pm\infty} f(x)=-\infty$ (по параболам).

6) Чётность/нечётность и периодичность

• $f(-x)$ не равна ни $f(x)$, ни $-f(x)$ (например, $f(1)=\sin1>0$, но $f(-1)=-1$), значит функция ни чётная, ни нечётная.
• Из кусочного определения с параболами вне $[0,\pi]$ следует отсутствие периода: не является периодической.

7) Вогнутость (конкавность)

По вторым производным:

• На $(-\infty,0)$: $f»(x)=-2<0$ ⇒ вогнута вниз.
• На $(0,\pi)$: $f»(x)=-\sin x\le 0$ ⇒ вогнута вниз (строго — на $(0,\pi)\setminus\{0,\pi\}$).
• На $(\pi,+\infty)$: $f»(x)=-2<0$ ⇒ вогнута вниз.

Важно: хотя каждая ветвь вогнута вниз, на всей $\mathbb R$ функция не является вогнутой, потому что в узлах производная подпрыгивает вверх: $f’_-(0)=0<f’_+(0)=1$ и $f’_-(\pi)=-1<f’_+(\pi)=0$. Для глобальной вогнутости производная должна быть невозрастающей; здесь это нарушено.

8) Краткая сводка свойств (для проверки)

• $D(f)=\mathbb R$, $E(f)=(-\infty,1]$.
• Непрерывна на $\mathbb R$, но не дифференцируема в $x=0,\pi$.
• Возрастает на $(-\infty,\tfrac{\pi}{2}]$, убывает на $[\tfrac{\pi}{2},\infty)$.
• Единственный глобальный максимум: $x=\tfrac{\pi}{2}$, $f=1$.
• $f>0$ на $(0,\pi)$, $f<0$ на $(-\infty,0)\cup(\pi,\infty)$.
• Нули: $x=0$ и $x=\pi$.
• Ограничена сверху, не ограничена снизу.
• Ни чётная, ни нечётная; не периодическая.
• Кусочно вогнута вниз; глобально не вогнута.