ГДЗ 10-11 Класс Номер 10.20 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Дана функция $y = f(x)$, где

$$f(x)=\{\begin{array}{ll}\sin (x+\frac{\pi }{2}),& \text{если }-\frac{3\pi }{2}\le x\le 0\\ x+1,& \text{если }0<x<2\\ -\sqrt{x-2}+3,& \text{если }x\ge 2\end{array}$$

а) Вычислите:

$$f(0) = \sin \left( 0 + \frac{\pi}{2} \right) = \sin \frac{\pi}{2} = 1;$$ $$f(6) = -\sqrt{6 — 2} + 3 = -\sqrt{4} + 3 = 1;$$ $$f(-\pi -2)$$

б) Постройте график функции $y = f(x)$;

в) Прочитайте график функции $y = f(x)$.

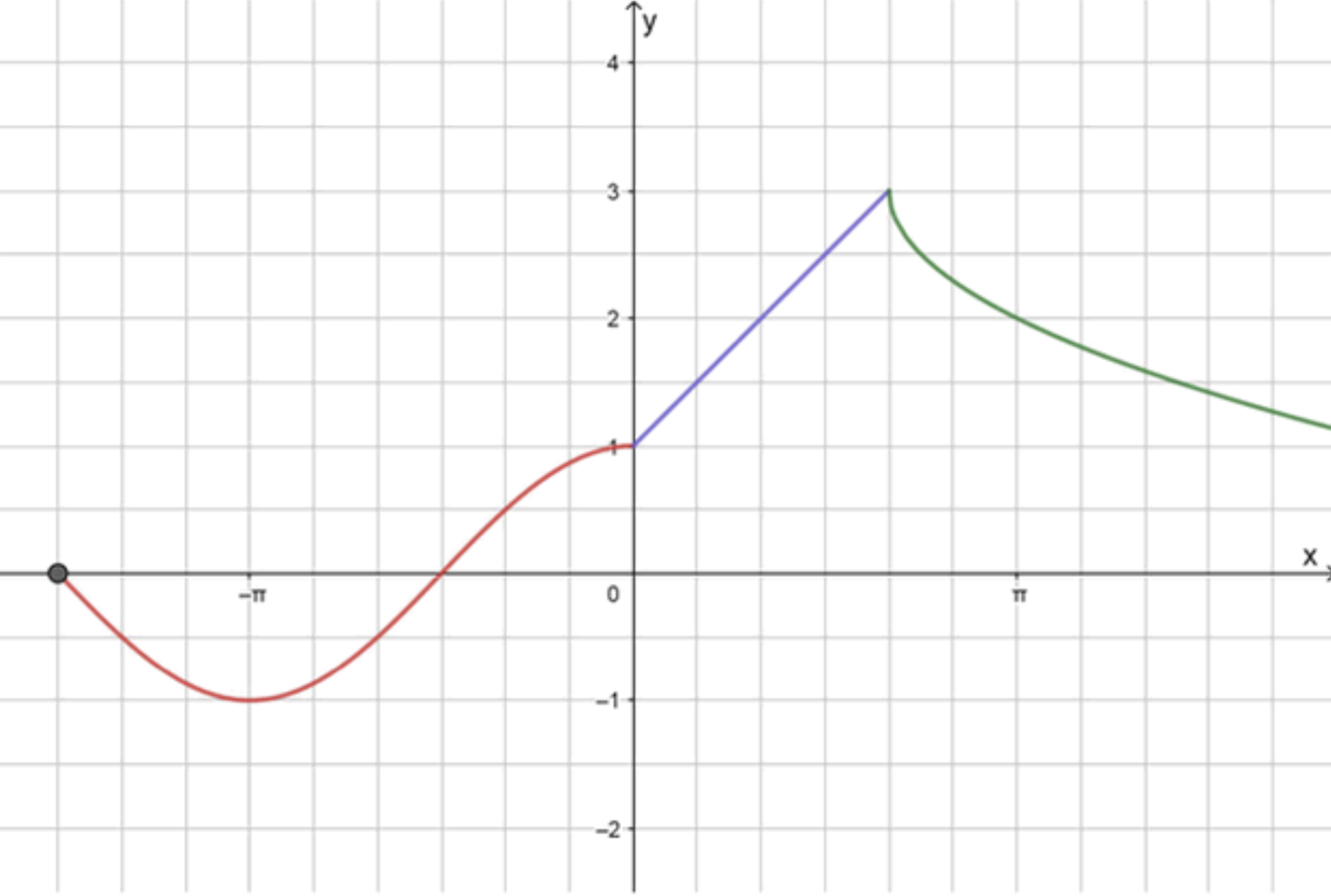
Дана функция:

$$f(x) = \begin{cases} \sin \left( x + \frac{\pi}{2} \right), & \text{если } -\frac{3\pi}{2} \leq x \leq 0 \\ x + 1, & \text{если } 0 < x < 2 \\ -\sqrt{x — 2} + 3, & \text{если } x \geq 2 \end{cases}$$

а) Найдем значения:

$$f(0) = \sin \left( 0 + \frac{\pi}{2} \right) = \sin \frac{\pi}{2} = 1;$$ $$f(6) = -\sqrt{6 — 2} + 3 = -\sqrt{4} + 3 = 1;$$ $$f(-\pi — 2) — \text{нет};$$

б)

• $y = \sin \left( x + \frac{\pi}{2} \right)$ — уравнение синусоиды:

$$\begin{array}{|c|c|c|c|c|} \hline x & -\frac{3\pi}{2} & -\pi & -\frac{\pi}{2} & 0 \\ \hline y & 0 & -1 & 0 & 1 \\ \hline \end{array}$$

• $y = x + 1$ — уравнение прямой:

$$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 1 & 3 \\ \hline \end{array}$$

• $y = -\sqrt{x — 2} + 3$ — ветвь параболы:

$$x_0 = 2, \; y_0 = 3;$$ $$\begin{array}{|c|c|c|c|} \hline x & 2 & 3 & 6 \\ \hline y & 3 & 2 & 1 \\ \hline \end{array}$$

График функции:

в) Свойства функции:

• $D(f) = \left[ -\frac{3\pi}{2}; +\infty \right); \; E(f) = (-\infty; 3];$
• Возрастает на $[- \pi; 2]$;
• Убывает на $\left[ -\frac{3\pi}{2}; -\pi \right] \cup [2; +\infty)$;
• $f(x) > 0$ на $\left( -\frac{\pi}{2}; 11 \right)$;
• $f(x) < 0$ на $\left( -\frac{3\pi}{2}; -\frac{\pi}{2} \right) \cup (11; +\infty)$;
• Ограничена сверху;
• $y_{\max} = y(2) = 3$;
• Ни четная, ни нечетная;
• Не является периодической;
• Непрерывна на $\left[ -\frac{3\pi}{2}; +\infty \right)$.

Дано:

$$f(x)= \begin{cases} \sin\!\bigl(x+\tfrac{\pi}{2}\bigr), & -\tfrac{3\pi}{2}\le x\le 0,\\[2mm] x+1, & 0<x<2,\\[2mm] -\sqrt{x-2}+3, & x\ge 2. \end{cases}$$

Область определения складывается из трёх участков:

• первый кусок задан на $\left[-\tfrac{3\pi}{2},\,0\right]$;
• второй — на $(0,2)$;
• третий — на $[2,+\infty)$.

Промежуток $x=0$ включён в первый кусок, $x=2$ — в третий. Пробелов нет.
Итог: $D(f)=\left[-\tfrac{3\pi}{2},+\infty\right)$.

Численные ориентиры:

$$-\tfrac{3\pi}{2}\approx -4{,}712,\quad -\tfrac{\pi}{2}\approx -1{,}571,\quad \pi\approx 3{,}142.$$

а) вычисление значений

• $f(0)$. Точка $0$ принадлежит первому куску.
  $\displaystyle f(0)=\sin\!\Bigl(0+\tfrac{\pi}{2}\Bigr)=\sin\tfrac{\pi}{2}=1.$
• $f(6)$. Число $6\ge 2\Rightarrow$ третий кусок:
  $\displaystyle f(6)=-\sqrt{6-2}+3=-\sqrt{4}+3=-2+3=1.$
• $f(-\pi-2)$. Число $-\pi-2\approx -5{,}142$ меньше левой границы $-\tfrac{3\pi}{2}\approx -4{,}712$.
  Следовательно, эта точка не входит в область определения. Значение не существует.

в) Подробное исследование каждого куска

(I) $y=\sin\!\bigl(x+\tfrac{\pi}{2}\bigr)$, $x\in\left[-\tfrac{3\pi}{2},0\right]$

Удобно сделать замену $u=x+\tfrac{\pi}{2}$. Тогда при $x\in\left[-\tfrac{3\pi}{2},0\right]$ имеем

$$u\in\left[-\pi,\;\tfrac{\pi}{2}\right].$$

На этом промежутке $\sin u$:

• убывает на $[-\,\pi,\,-\,\tfrac{\pi}{2}]$ (от $0$ до $-1$);
• возрастает на $[-\,\tfrac{\pi}{2},\,\tfrac{\pi}{2}]$ (от $-1$ до $1$).

Ключевые точки и значения:

$$\begin{aligned} x&=-\tfrac{3\pi}{2}\Rightarrow u=-\pi,\quad &&f=0;\\ x&=-\pi\Rightarrow u=-\tfrac{\pi}{2},\quad &&f=-1\quad(\text{локальный минимум на этом куске});\\ x&=-\tfrac{\pi}{2}\Rightarrow u=0,\quad &&f=0;\\ x&=0\Rightarrow u=\tfrac{\pi}{2},\quad &&f=1. \end{aligned}$$

Знаки на куске:
$f>0$ при $x\in(-\tfrac{\pi}{2},\,0]$, $f=0$ при $x=-\tfrac{3\pi}{2},\,-\tfrac{\pi}{2}$, $f<0$ при $x\in(-\tfrac{3\pi}{2},-\tfrac{\pi}{2})$.

Монотонность на куске:
убывает на $\left[-\tfrac{3\pi}{2},-\pi\right]$, возрастает на $\left[-\pi,0\right]$.

(II) $y=x+1$, $x\in(0,2)$

Линейная функция с угловым коэффициентом $1$ — строго возрастающая.
Значения на конце: слева $f(0^+)=1$ (точка открыта), справа $f(2^-)=3$ (тоже открыта).

Знаки на куске: $f(x)=x+1>1$ для всех $x\in(0,2)$, значит $f>0$ на всём куске.

Монотонность: строго возрастает на $(0,2)$.

(III) $y=-\sqrt{x-2}+3$, $x\in[2,+\infty)$

Это корневая ветвь (не парабола): берём $y=3-\sqrt{x-2}$.
$\sqrt{x-2}$ возрастает, значит $3-\sqrt{x-2}$ строго убывает.

Ключевые точки:

$$x=2\Rightarrow f(2)=3\quad(\text{максимум для этого куска и для всей функции});$$ $$x=11\Rightarrow f(11)=3-\sqrt{9}=0;$$

при $x\to+\infty$: $\sqrt{x-2}\to+\infty\Rightarrow f(x)\to-\infty$.

Знаки на куске:
$f>0$ при $2\le x<11$, $f=0$ при $x=11$, $f<0$ при $x>11$.

Монотонность: строго убывает на $[2,+\infty)$.

Стыки и непрерывность

В точке $x=0$

• Значение слева: $f(0)=\sin(\pi/2)=1$ (точка включена в 1-й кусок).
• Правый предел: $\lim\limits_{x\to 0+}(x+1)=1$.
• Совпадают и сходимся к включённой точке $\Rightarrow$ непрерывно в $x=0$.

Производные:

• слева $f’_-(0)=\cos(0+\tfrac{\pi}{2})=0$;
• справа $f’_+(0)=1$.
  Производные не равны $\Rightarrow$ в $x=0$ не дифференцируема (излом).

В точке $x=2$

• Левый предел: $\lim\limits_{x\to 2-}(x+1)=3$.
• Значение и правый предел: $f(2)=3$, $\lim\limits_{x\to 2+}\bigl(-\sqrt{x-2}+3\bigr)=3$.
  Совпадают $\Rightarrow$ непрерывно в $x=2$.

Производные:

• слева $f’_-(2)=1$;
• справа $f’_+(2)=\displaystyle -\frac{1}{2\sqrt{x-2}}\Big|_{x\to 2+}\to -\infty$.
  $\Rightarrow$ не дифференцируема в $x=2$ (резкий «угол»).

Итог: каждое звено непрерывно на своём интервале, склейки согласованы по пределам, значит

$$\boxed{\;f\ \text{непрерывна на}\ \left[-\tfrac{3\pi}{2},+\infty\right)\;}$$

и дважды недифференцируема в точках $x=0$ и $x=2$.

Монотонность на всей оси

Собираем из кусков:

• убывает на $\left[-\tfrac{3\pi}{2},-\pi\right]$;
• возрастает на $\left[-\pi,0\right]$ и на $(0,2)$ (вместе это дает монотонный подъём от $-\pi$ до $2$);
• убывает на $[2,+\infty)$.

Часто это формулируют кратко:

$$\text{возрастает на }[-\pi,2],\quad \text{убывает на }\left[-\tfrac{3\pi}{2},-\pi\right]\cup[2,+\infty).$$

(строго говоря, «строго возрастает» — на $[-\,\pi,0]$ и $(0,2)$ отдельно; объединение $[-\,\pi,2]$ удобно как сводка).

Экстремумы и ограниченность

• Глобальный максимум достигается в $x=2$: $\boxed{y_{\max}=f(2)=3}$.
• Глобального минимума нет (ветвь $3-\sqrt{x-2}$ уходит в $-\infty$).

Ограниченность:

• сверху: да, $f(x)\le 3$;
• снизу: нет.

Локальные особенности:

• на первом куске локальный минимум $f=-1$ при $x=-\pi$;
• точка $x=0$ не является локальным максимумом всей функции (справа $f$ ещё растёт);
• $x=2$ — локальный и глобальный максимум.

Множество значений (образ)

• первый кусок даёт $[-1,1]$;
• второй — $(1,3)$;
• третий — $(-\infty,3]$.

Объединяя:

$$\boxed{\;E(f)=(-\infty,\,3]\;}$$

Нули и знаки функции

Решаем $f(x)=0$ по кускам:

• $\sin\!\bigl(x+\tfrac{\pi}{2}\bigr)=0$ $\Rightarrow x+\tfrac{\pi}{2}=k\pi$.
  На отрезке $\left[-\tfrac{3\pi}{2},0\right]$ это даёт $x=-\tfrac{3\pi}{2}$ и $x=-\tfrac{\pi}{2}$.
• $x+1=0$ $\Rightarrow x=-1$ — вне $(0,2)$, не подходит.
• $-\sqrt{x-2}+3=0$ $\Rightarrow \sqrt{x-2}=3 \Rightarrow x=11$ (подходит, т.к. $11\ge 2$).

Итак, нули: $\boxed{x\in\left\{-\tfrac{3\pi}{2},\,-\tfrac{\pi}{2},\,11\right\}}$.

Знаковая картина:

$$\begin{aligned} &f(x)>0 \ \text{на}\ \left(-\tfrac{\pi}{2},\,11\right),\\ &f(x)=0 \ \text{при}\ x=-\tfrac{3\pi}{2},\ -\tfrac{\pi}{2},\ 11,\\ &f(x)<0 \ \text{на}\ \left(-\tfrac{3\pi}{2},-\tfrac{\pi}{2}\right)\cup(11,+\infty). \end{aligned}$$

Чётность и периодичность

• Чётность/нечётность: область определения не симметрична относительно нуля, а сами формулы на разных частях разные. Следовательно, $f$ ни чётная, ни нечётная.
• Периодичность: из-за линейного и корневого кусков функция не периодична.

Итог по формулировкам из условия

• $D(f)=\left[-\tfrac{3\pi}{2},+\infty\right)$, $E(f)=(-\infty,3]$;
• возрастание: на $[-\,\pi,0]$ и $(0,2)$ (в совокупности — $[-\,\pi,2]$);
• убывание: на $\left[-\tfrac{3\pi}{2},-\pi\right]$ и $[2,+\infty)$;
• $f(x)>0$ на $\left(-\tfrac{\pi}{2},11\right)$;
• $f(x)<0$ на $\left(-\tfrac{3\pi}{2},-\tfrac{\pi}{2}\right)\cup(11,+\infty)$;
• сверху ограничена, $\,y_{\max}=3$ при $x=2$;
• не чётная и не нечётная; не периодическая; непрерывна на $\left[-\tfrac{3\pi}{2},+\infty\right)$;
• дополнение: функция не дифференцируема в точках $x=0$ и $x=2$.

б)