Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 10.21 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Решите графически уравнение:
а)
б)
в)
г)
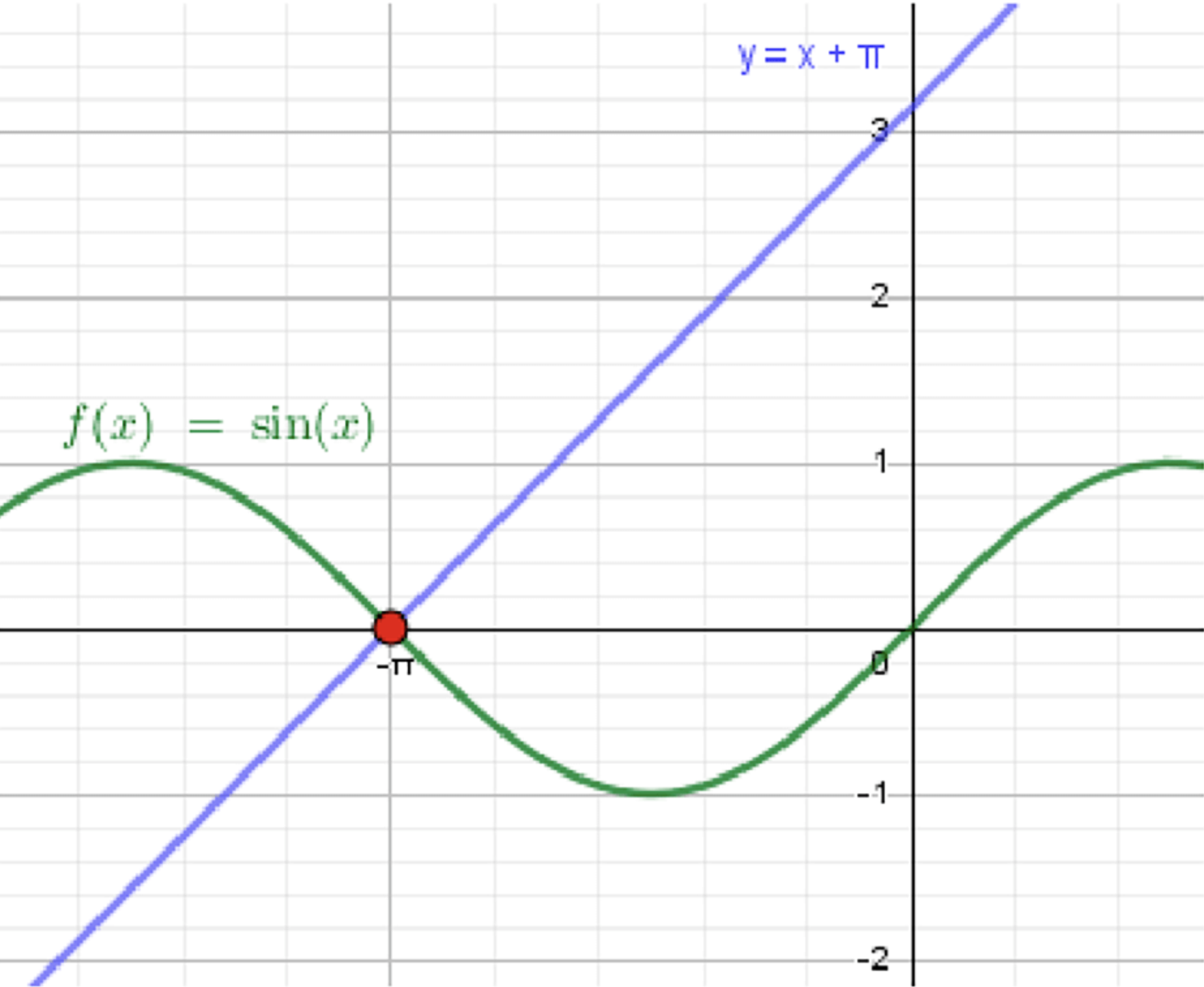
Решить графически уравнение:
а) ;
— уравнение синусоиды;
— уравнение прямой:
| 0 | ||
|---|---|---|
| 0 | ≈ 3 |
Графики функций:
Ответ: .
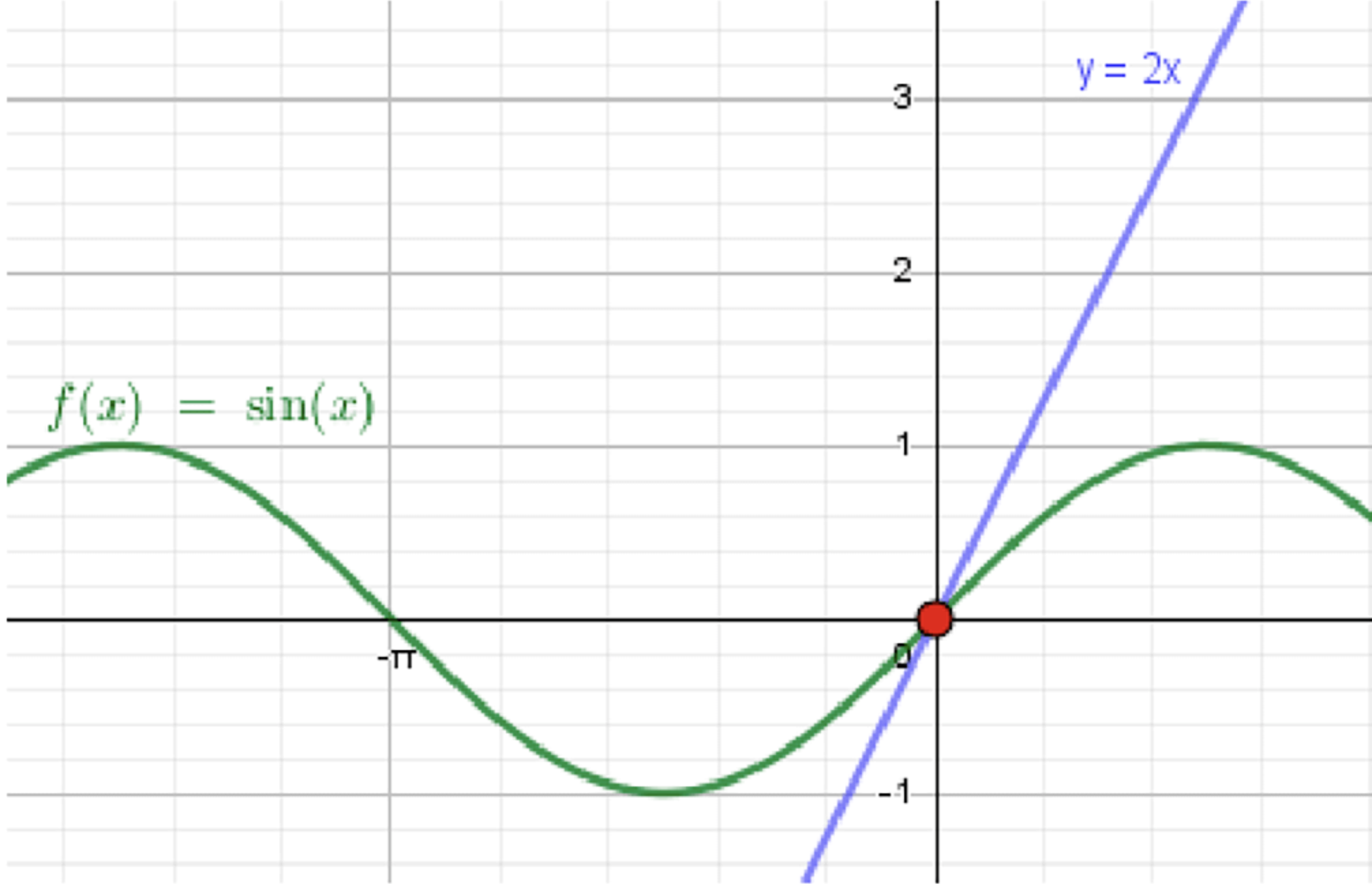
б) ;
— уравнение синусоиды;
— уравнение прямой:
| 0 | 1 | |
|---|---|---|
| 0 | 2 |
Графики функций:
Ответ: .
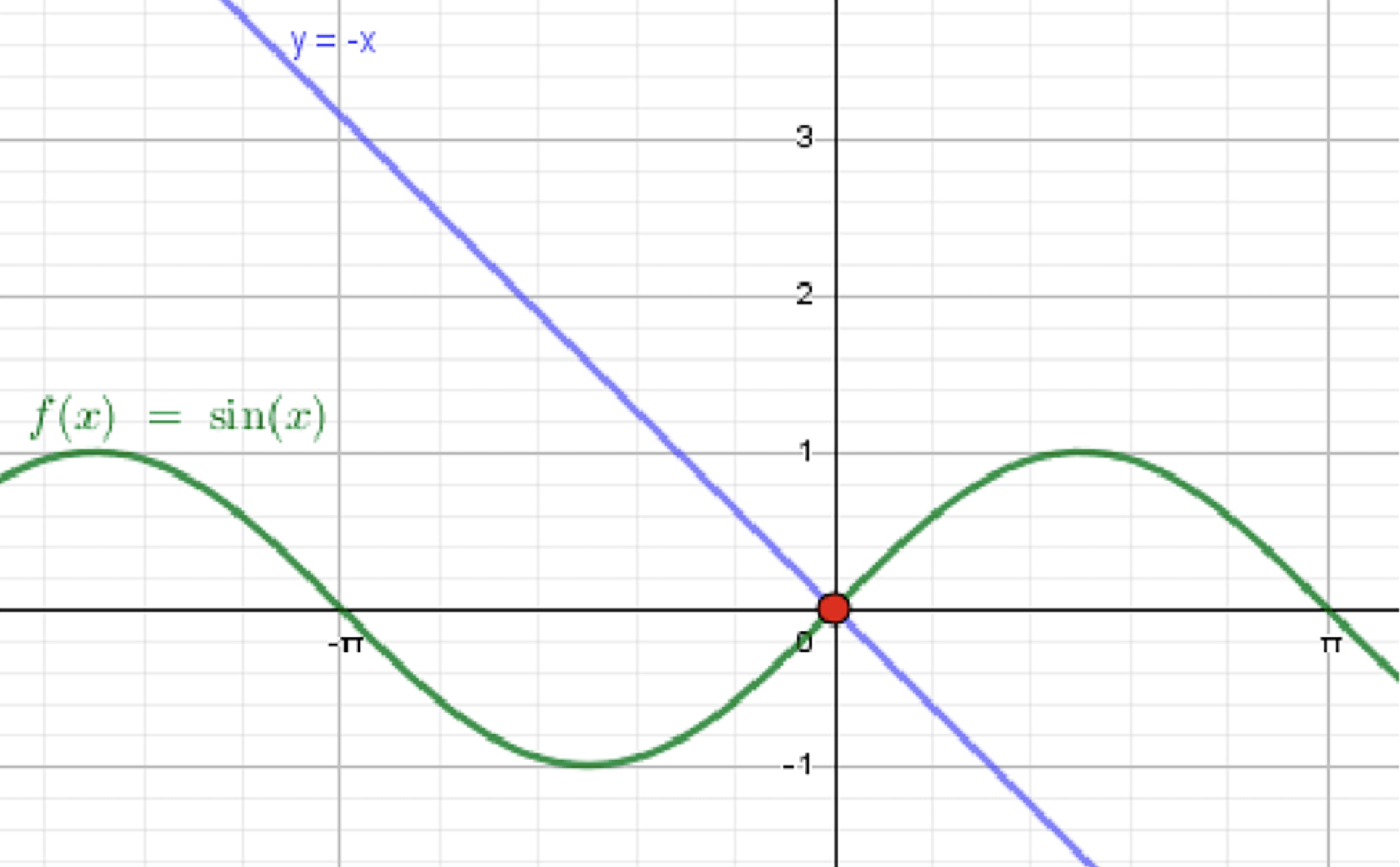
в) ;
— уравнение синусоиды;
— уравнение прямой:
| 0 | 1 | |
|---|---|---|
| 0 | -1 |
Графики функций:
Ответ: .
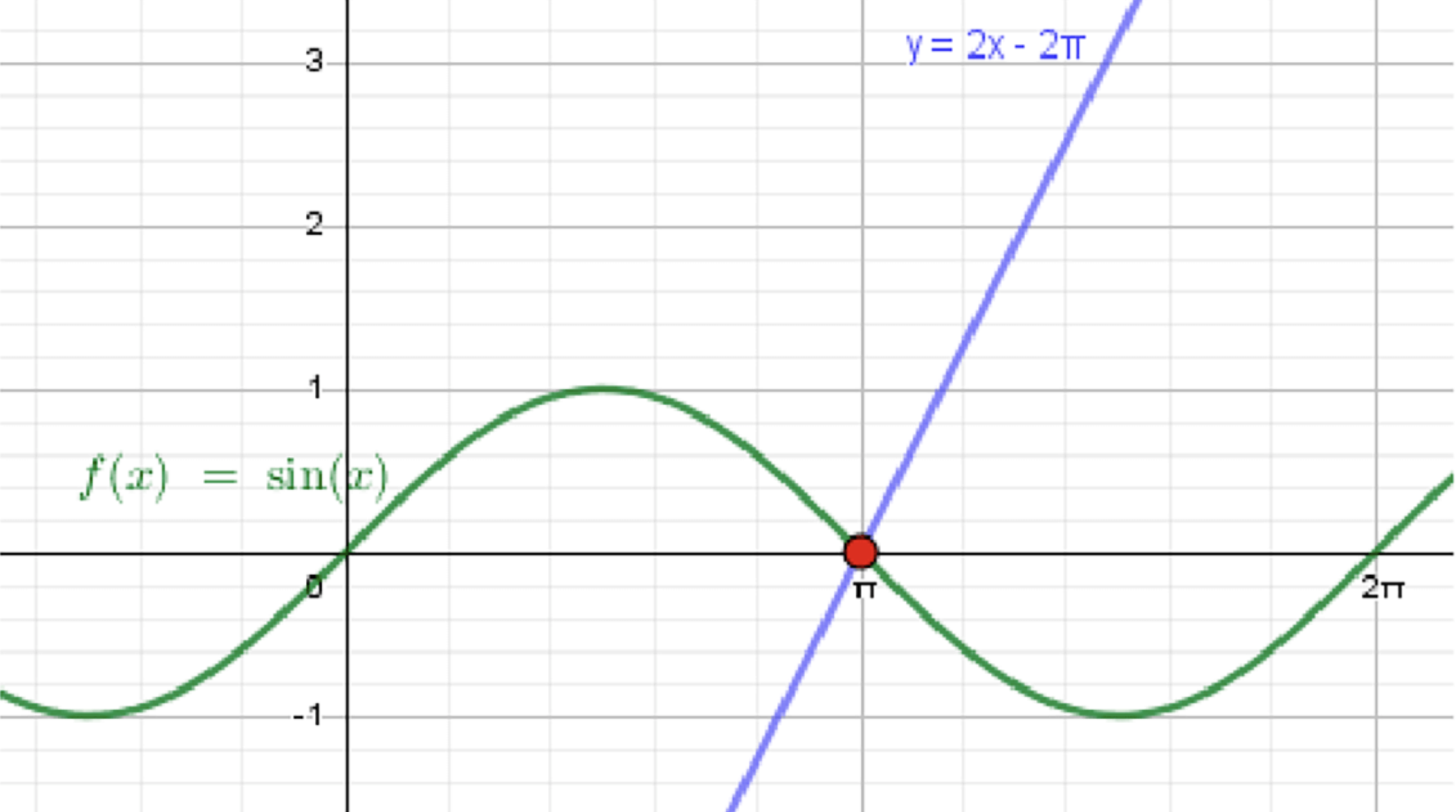
г) ;
— уравнение синусоиды;
— уравнение прямой:
| ≈ -1 | 0 |
Графики функций:
Ответ: .
а)
Идея графически. Строим на одной системе координат:
- синусоиду (лежит между и );
- прямую (наклон , пересекает ось в точке ).
Ограничение области поиска. Так как , из равенства следует
Значит, возможные точки пересечения — только в узком интервале длины вокруг .
Точная проверка конкретной точки.
Единственность (почему больше пересечений нет). Рассмотрим функцию
Тогда для всех , причём равенство только когда (точки ). Следовательно, строго убывает (производная не положительна и отрицательна на любом непустом интервале). Убывающая непрерывная функция может иметь не более одного нуля. Мы уже нашли , значит он единственный.
Вывод. .
б)
Графически. Синусоида и прямая (наклон , проходит через начало координат).
Ограничение области. .
За пределами этого отрезка прямая имеет по модулю значение больше 1, с синусоидой пересечений быть не может.
Точная точка.
Единственность. Пусть . Тогда
Значит, строго убывает на всей , а у строго убывающей функции не может быть более одного нуля. Так как уже найден, он единственный.
Вывод. .
в)
Графически. Сравниваем синусоиду с прямой (наклон , через начало координат). Видно очевидное пересечение в нуле.
Ограничение области. Из и следует . Значит, искать нужно только на .
Точная точка.
Единственность — два надёжных аргумента (любой из них достаточен).
- Монотонность функции .
всегда (равно 0 лишь при , то есть в отдельных точках ). Следовательно, неубывает везде и строго возрастает на любом интервале ненулевой длины. У такой функции не более одного нуля. Ноль при найден — он единственный. - Липшицевость синуса (чуть более «жёсткое» обоснование).
Для любых : . Тогдаи строгий знак «» достигается на любом интервале, потому что не может быть линейной с наклоном на отрезке. Значит, строго возрастает ⇒ ноль единственный.
Вывод. .
г)
Графически. Синусоида и прямая (наклон , пересечение с осью в ). Визуально видно пересечение в .
Ограничение области. . Ищем только в окрестности .
Точная точка.
Единственность. Пусть . Тогда
то есть строго убывает на всей . Стало быть, ноль только один — мы его нашли при .
Вывод. .
Финальный ответ:
Что мы сделали «графически» и почему это строго:
- Сначала сузили область поиска, используя диапазон — это и есть ключ к быстрому построению эскизов и пониманию, где вообще возможно пересечение с прямой.
- Затем для каждой разности «синусоида − прямая» посмотрели на производную:
, , .
Во всех четырёх случаях получили монотонность (в трёх — строгую убываемость, в одном — строгую возрастаемость), что даёт единственность решения. - Наконец, нашли точку, где равенство выполняется точно (без приближений), — это и есть наш единственный корень в каждой задаче.