Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 10.23 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Решите графически уравнение:
а)
б)
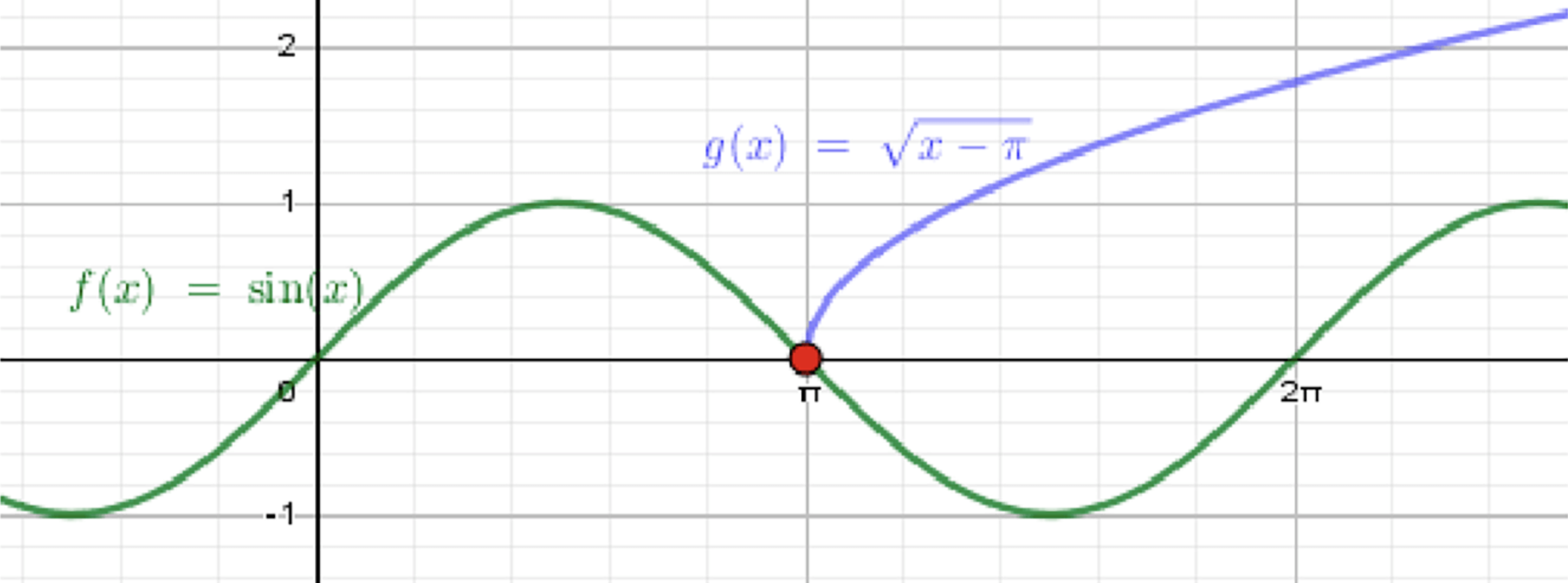
Решить графически уравнение:
а)
— уравнение синусоиды;
— ветвь параболы:
Графики функций:
Ответ: .
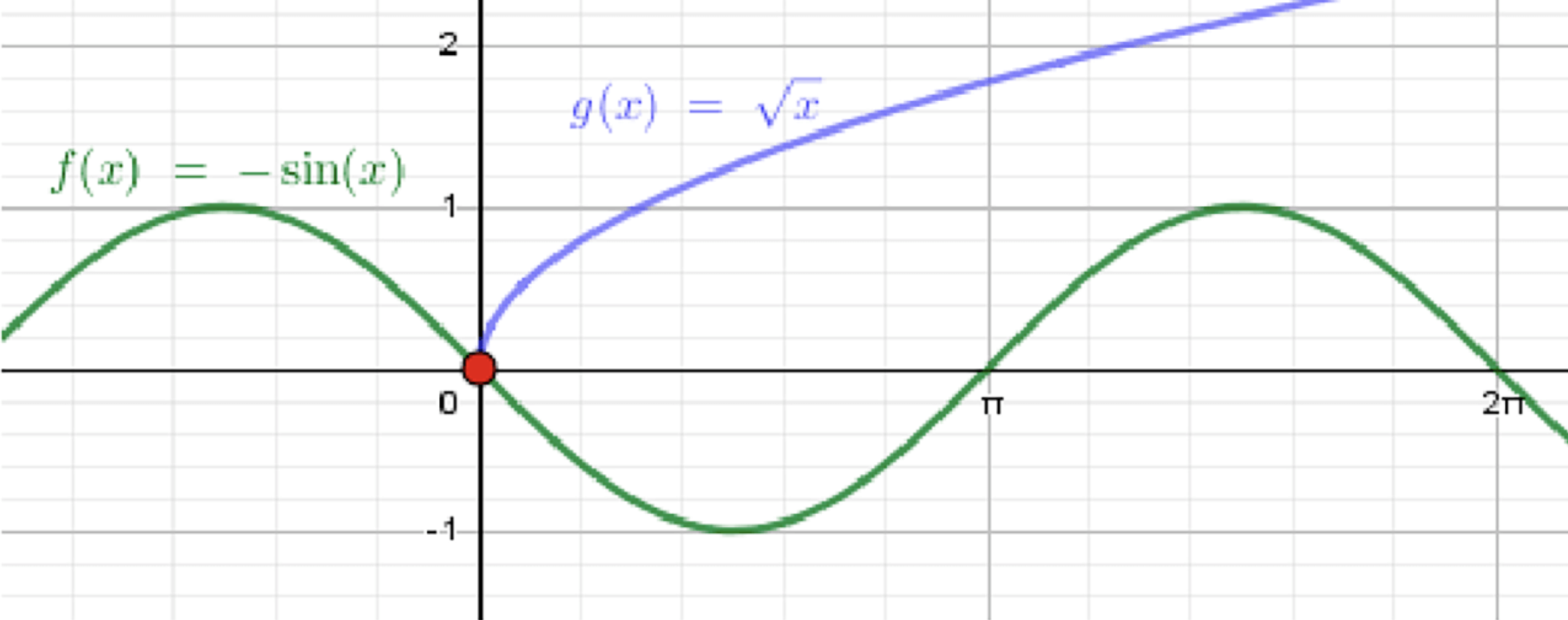
б)
— уравнение синусоиды;
— ветвь параболы:
Графики функций:
Ответ: .
а) (то же, что )
1) Область определения и первые следствия
- Из следует: .
- Правая часть , значит и левая часть должна быть неотрицательной: .
Итак, ищем такие, что одновременно:
- ;
- .
Напомним: на интервалах вида , .
Из них при первый «положительный» интервал — это ; на синус отрицателен.
2) Квадратирование с контролем условий
Раз равны неотрицательные величины, можно возвести в квадрат (эквивалентно при нашем контроле знаков):
Так как , получаем двойное неравенство для :
Отсюда
Итак, обязательно .
3) Сопоставим с знаком на найденном отрезке
На синус отрицателен, а (ведь ).
Следовательно, на всём имеем , а правая часть . Равенство невозможно.
Остаётся крайняя точка :
4) Почему других решений точно нет
- На — знак разный (см. п.3).
- Начиная с : , тогда как . На любом интервале, где (то есть ), правая часть строго больше 1, а левая — пересечений нет.
Итог по (а): единственное решение
б) (то же, что )
1) Область определения и знаки
- Из следует: .
- Правая часть равна . Значит, тоже должен быть .
Итак, ищем , для которых .
2) Ограничение по амплитуде синуса
Так как , получаем
Следовательно, любой возможный корень обязан лежать в узком отрезке .
3) Знак на
На интервале синус положителен. Поскольку , то на всём имеем , а правая часть . Равенство невозможно.
Проверим граничную точку :
4) Почему вне решений нет
- Для : , но . Совпасть они не могут (равенство слева достигается лишь у синуса при , но тогда вовсе не равен 1, и правая часть не ).
- Для корень не определён в вещественных числах.
Итог по (б): единственное решение
Короткое графическое резюме
- В (а) графики и касаются в точке ; далее ветвь сразу «уходит» выше уровня 1, поэтому больше пересечений нет.
- В (б) графики и пересекаются только в начале координат: около нуля (для ), тогда как . Для ветвь опускается ниже , где уже не бывает.
Ответы:
а) .
б) .