ГДЗ 10-11 Класс Номер 10.24 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Решите графически уравнение:

а) $\sin (x-\frac{\pi }{3})=\pi -3x$

б) $\sin (x+\frac{\pi }{6})={(x-\frac{\pi }{3})}^2+1$

Решить графически уравнение:

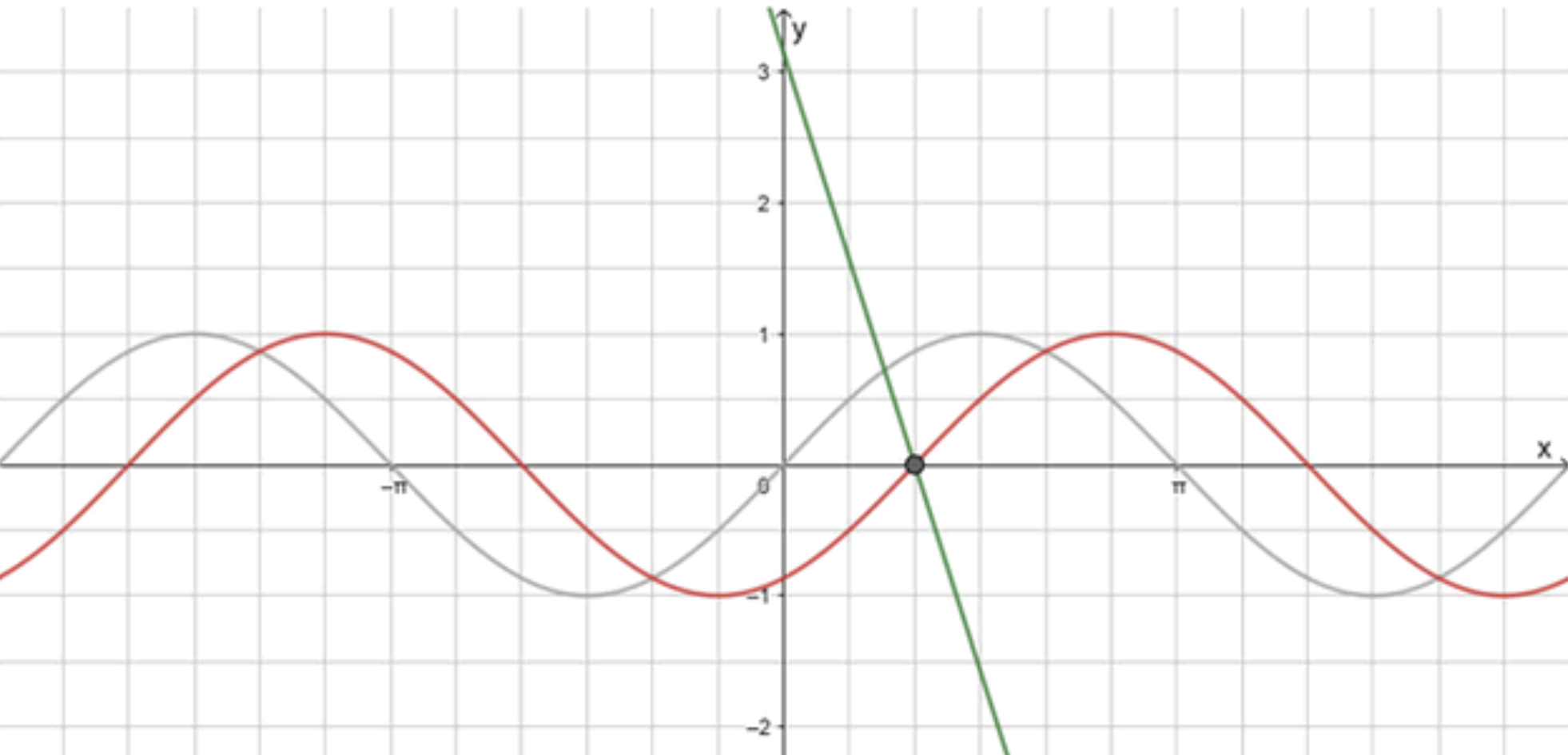
а) $\sin\left(x — \frac{\pi}{3}\right) = \pi — 3x$

$y = \sin\left(x — \frac{\pi}{3}\right)$ — уравнение синусоиды;

$y = \pi — 3x$ — уравнение прямой:

Графики функций:

Ответ: $x = \frac{\pi}{3}$.

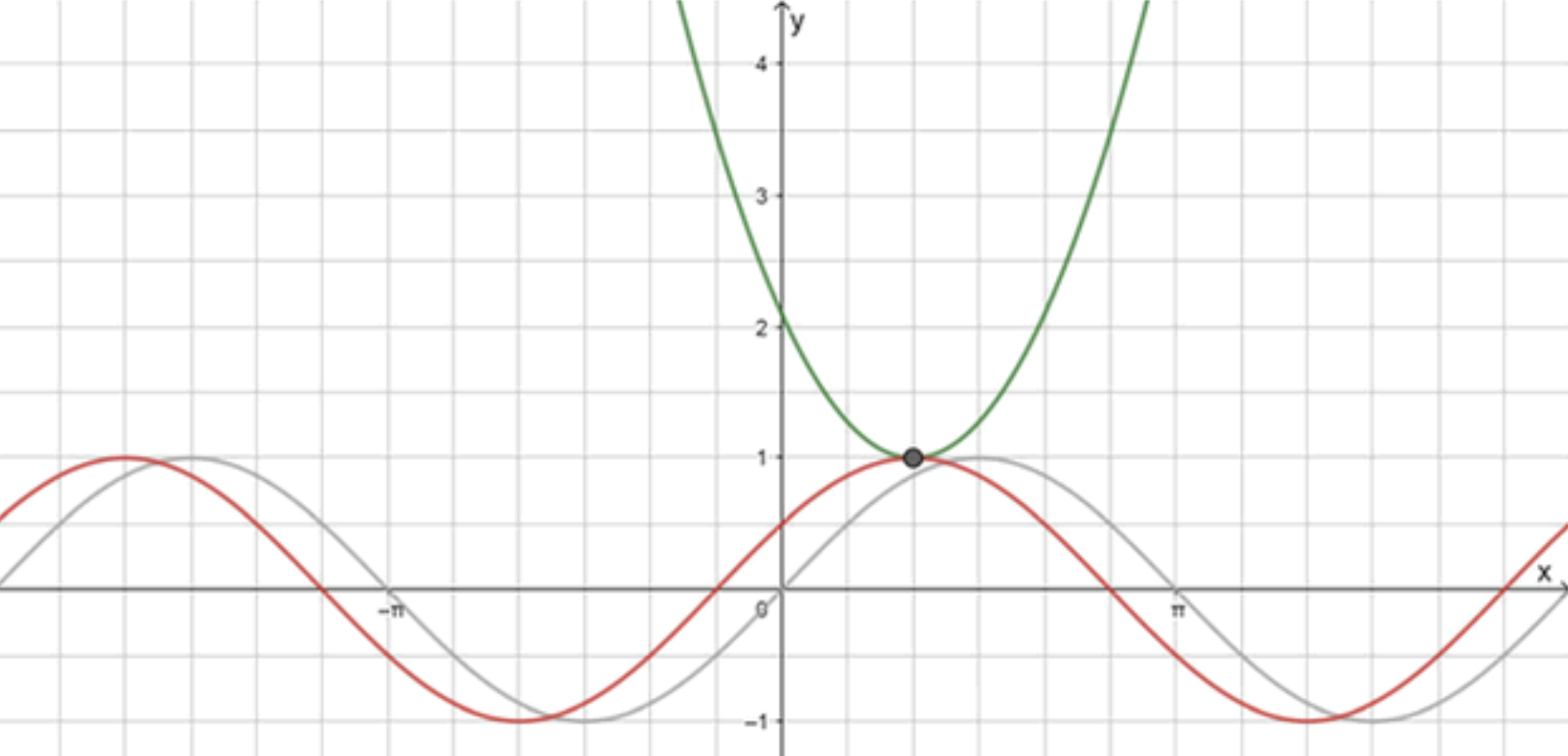
б) $\sin\left(x + \frac{\pi}{6}\right) = \left(x — \frac{\pi}{3}\right)^2 + 1$

$y = \sin\left(x + \frac{\pi}{6}\right)$ — уравнение синусоиды;

$y = \left(x — \frac{\pi}{3}\right)^2 + 1$ — уравнение параболы:

$x_0 = \frac{\pi}{3}, \, y_0 = 1$;

Графики функций:

Ответ: $x = \frac{\pi}{3}$.

а)

Задача

$$\sin\!\left(x-\frac{\pi}{3}\right)=\pi-3x.$$

1) Диапазон возможных $x$ из-за ограничения синуса

Левая часть лежит в отрезке $[-1,1]$. Значит правая тоже должна туда попадать:

$$-1\le \pi-3x\le 1.$$

Решим двойное неравенство:

$$\begin{aligned} &\pi-3x\le 1 \;\;\Longleftrightarrow\;\; -3x\le 1-\pi \;\;\Longleftrightarrow\;\; x\ge \frac{\pi-1}{3},\\[2mm] &-1\le \pi-3x \;\;\Longleftrightarrow\;\; -1-\pi\le -3x \;\;\Longleftrightarrow\;\; x\le \frac{\pi+1}{3}. \end{aligned}$$

Итак,

$$x\in \left[\frac{\pi-1}{3},\;\frac{\pi+1}{3}\right].$$

Это узкий отрезок вокруг $x=\frac{\pi}{3}$ (примерно $[0.714,\;1.381]$).

2) Удобная подстановка

Положим

$$t=x-\frac{\pi}{3}.$$

Тогда $x=t+\frac{\pi}{3}$, и

$$\sin \text{\hspace{0.17em}⁣}(x-\frac{\pi }{3})=\sin t,$$

$$\sin\!\left(x-\frac{\pi}{3}\right)=\sin t,\qquad \pi-3x=\pi-3\!\left(t+\frac{\pi}{3}\right)=\pi-3t-\pi=-3t.$$

Уравнение упрощается до

$$\sin t=-3t\quad\Longleftrightarrow\quad f(t)=\sin t+3t=0.$$

Из шага (1) ещё и видно, что любой корень обязан удовлетворять $t\in[-\tfrac13,\tfrac13]$, но сейчас нам это уже не критично.

3) Единственность корня (строгая монотонность)

Проверим производную:

$$f'(t)=\cos t+3.$$

Так как $\cos t\ge -1$ при всех $t$, то

$$f'(t)\ge -1+3=2>0 \quad\text{для всех } t\in\mathbb R.$$

Следовательно, $f(t)$ строго возрастает на всей прямой, значит у него может быть не более одного нуля.

4) Нахождение корня

Очевидно,

$$f(0)=\sin 0+3\cdot 0=0 \;\;\Longrightarrow\;\; t=0 \text{ — корень.}$$

Из пункта (3) он единственный.

Возвращаемся к $x$:

$$t=0\;\Longrightarrow\; x=\frac{\pi}{3}.$$

5) Геометрическая картина и проверка

• На нашем отрезке $x\in[(\pi-1)/3,(\pi+1)/3]$ график $y=\sin(x-\pi/3)$ слегка возрастает (аргумент меняется в $[-1/3,1/3]$, где $\cos>0$).
• Прямая $y=\pi-3x$ убывает со скоростью 3, проходя через $(\pi/3,0)$.
• Пересечение ровно одно — в точке $\bigl(\tfrac{\pi}{3},0\bigr)$.

Проверка подстановкой:

$$\sin\!\left(\tfrac{\pi}{3}-\tfrac{\pi}{3}\right)=\sin 0=0,\qquad \pi-3\cdot \tfrac{\pi}{3}=\pi-\pi=0.$$

Ответ к (а): $\displaystyle x=\frac{\pi}{3}$ (единственный корень).

б)

Задача

$$\sin\!\left(x+\frac{\pi}{6}\right)=\left(x-\frac{\pi}{3}\right)^2+1.$$

1) Моментально сузим поиск по значениям

Левая часть $\in[-1,1]$, правая часть $\ge 1$ (минимум параболы равен $1$). Поэтому равенство возможно только когда обе части равны $1$.

То есть необходимо одновременно:

$$\sin\!\left(x+\frac{\pi}{6}\right)=1 \quad\text{и}\quad \left(x-\frac{\pi}{3}\right)^2+1=1.$$

Второе даёт

$$\left(x-\frac{\pi}{3}\right)^2=0\;\;\Longrightarrow\;\; x=\frac{\pi}{3}.$$

Проверяем первое при этом $x$:

$$\sin\!\left(\frac{\pi}{3}+\frac{\pi}{6}\right)=\sin\!\left(\frac{\pi}{2}\right)=1,$$

условие выполняется.

2) Альтернативное «чистое» доказательство единственности

Снова введём сдвиг $s=x-\frac{\pi}{3}$. Тогда

$$\sin\!\left(x+\frac{\pi}{6}\right)=\sin\!\left(s+\frac{\pi}{2}\right)=\cos s,$$

и уравнение эквивалентно

$$\cos s=s^2+1.$$

Но $\cos s\le 1$ при любых $s$, а $s^2+1\ge 1$ и строго $>1$ при $s\ne 0$.
Значит для любого $s\ne 0$ имеем $\cos s < s^2+1$ — равенство невозможно.
Следовательно, единственный шанс — $s=0$, т.е. $x=\frac{\pi}{3}$.

3) Локальная геометрия в точке пересечения

Посмотрим на производные в точке $x=\frac{\pi}{3}$:

• Для синуса: $y_1’=\cos\!\left(x+\frac{\pi}{6}\right)$, значит $y_1’\big|_{x=\pi/3}=\cos(\pi/2)=0$.
• Для параболы: $y_2’=2\!\left(x-\frac{\pi}{3}\right)$, значит $y_2’\big|_{x=\pi/3}=0$.

Обе кривые имеют общую горизонтальную касательную в точке $\bigl(\tfrac{\pi}{3},1\bigr)$.
Вторая производная разная по знаку:

$$y_1»=-\sin\!\left(x+\tfrac{\pi}{6}\right)\Rightarrow y_1»\big|_{x=\pi/3}=-1 \quad(\text{вогнута вниз}),$$ $$y_2»=2>0 \quad(\text{выпукла вверх}).$$

Разность $h(x)=y_1-y_2$ имеет $h(\pi/3)=0,\;h'(\pi/3)=0,\;h»(\pi/3)=-3<0$, то есть $\pi/3$ — локальный максимум разности; вокруг точки $h(x)<0$.
Отсюда видно, что кривые касаются и более не пересекаются.

Проверка подстановкой:

$$\sin\!\left(\tfrac{\pi}{3}+\tfrac{\pi}{6}\right)=1,\qquad \left(\tfrac{\pi}{3}-\tfrac{\pi}{3}\right)^2+1=1.$$

Ответ к (б): $\displaystyle x=\frac{\pi}{3}$ (единственный корень).

Итоги:

а) Единственный корень: $\boxed{x=\frac{\pi}{3}}$.

б) Единственный корень: $\boxed{x=\frac{\pi}{3}}$.

Геометрически:

а) синусоида (сдвиг вправо на $\pi/3$) и убывающая прямая пересекаются ровно один раз в $(\pi/3,0)$;

б) синусоида (сдвиг влево на $\pi/6$) и парабола $(x-\pi/3)^2+1$ касаются в $(\pi/3,1)$ и больше не пересекаются.