ГДЗ 10-11 Класс Номер 10.8 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y=\sin (x-\frac{\pi }{3});$

б) $y = \sin\left(x + \frac{\pi}{4}\right);$

в) $y = \sin(x — \pi);$

г) $y=\sin (x+\frac{\pi }{3})$

Построить график функции:

а) $y = \sin\left(x — \frac{\pi}{3}\right);$

Построим график функции $y = \sin x;$

Переместим его на $\frac{\pi}{3}$ единицы вправо:

б) $y = \sin\left(x + \frac{\pi}{4}\right);$

Построим график функции $y = \sin x;$

Переместим его на $\frac{\pi}{4}$ единицы влево:

в) $y = \sin(x — \pi);$

Построим график функции $y = \sin x;$

Переместим его на $\pi$ единиц вправо:

г) $y = \sin\left(x + \frac{\pi}{3}\right);$

Построим график функции $y = \sin x;$

Переместим его на $\frac{\pi}{3}$ единицы влево:

Общая идея (что происходит с графиком)

• Базовый график: $y=\sin x$. Амплитуда $A=1$, период $T=2\pi$, средняя линия $y=0$.
• Горизонтальный сдвиг: если в аргументе стоит $x-a$, график $y=\sin x$ сдвигается вправо на $a$; если $x+a$ — влево на $a$.
• Удобный «шаблон» пяти опорных точек для $y=\sin x$ за один период:

  $$(0,0),\quad \left(\tfrac{\pi}{2},1\right),\quad (\pi,0),\quad \left(\tfrac{3\pi}{2},-1\right),\quad (2\pi,0).$$

  После сдвига на $s$ по оси $x$ превращаем их в $(0+s,0),(\tfrac{\pi}{2}+s,1),(\pi+s,0),(\tfrac{3\pi}{2}+s,-1),(2\pi+s,0)$.

• Нули: $x = s + n\pi$. Максимумы: $x = s + \tfrac{\pi}{2} + 2\pi k$. Минимумы: $x = s + \tfrac{3\pi}{2} + 2\pi k$.
• Возрастание/убывание: $\sin(x-s)$ возрастает на интервалах $(s-\tfrac{\pi}{2}+2\pi k,\; s+\tfrac{\pi}{2}+2\pi k)$ и убывает на $(s+\tfrac{\pi}{2}+2\pi k,\; s+\tfrac{3\pi}{2}+2\pi k)$.

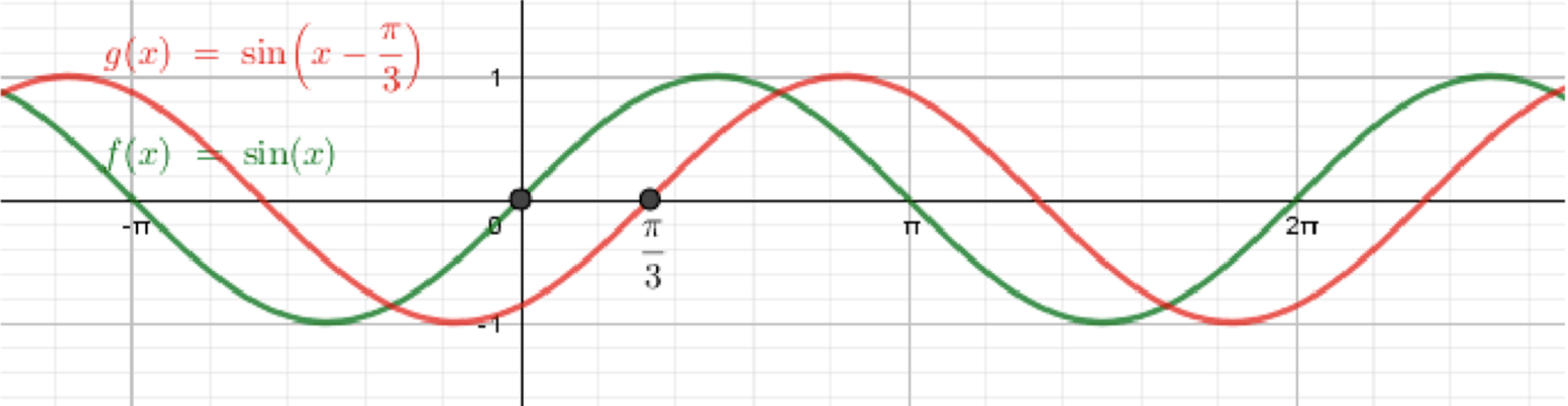
а) $y=\sin\!\left(x-\tfrac{\pi}{3}\right)$

Сдвиг: вправо на $s=\tfrac{\pi}{3}$. Амплитуда $1$, период $2\pi$, вертикальных сдвигов и растяжений нет.

Удобная шкала: отметьте кратные $\tfrac{\pi}{6}$ (т.к. $\tfrac{\pi}{3}=2\cdot\tfrac{\pi}{6}$).

Опорные точки (за один период):

$$(\frac{\pi }{3},0),(\frac{5\pi }{6},1),(\frac{4\pi }{3},0),$$

$$\left(\tfrac{\pi}{3},0\right),\quad \left(\tfrac{5\pi}{6},1\right),\quad \left(\tfrac{4\pi}{3},0\right),\quad \left(\tfrac{11\pi}{6},-1\right),\quad \left(\tfrac{7\pi}{3},0\right)\ (\text{последняя за }2\pi).$$

В пределах $[0,2\pi]$ используйте первые четыре.

Нули в $[0,2\pi]$: $x=\tfrac{\pi}{3},\ \tfrac{4\pi}{3}$.
Максимум: $x=\tfrac{5\pi}{6}$ (значение $1$).
Минимум: $x=\tfrac{11\pi}{6}$ (значение $-1$).

Возрастание: $(0,\tfrac{5\pi}{6})$ и $(\tfrac{11\pi}{6},2\pi)$.
Убывание: $(\tfrac{5\pi}{6},\tfrac{11\pi}{6})$.

Как чертить:

1. Проведите оси, по $x$ разметьте $0,\ \tfrac{\pi}{3},\ \tfrac{5\pi}{6},\ \tfrac{4\pi}{3},\ \tfrac{11\pi}{6},\ 2\pi$.
2. Поставьте точки: нули в $\tfrac{\pi}{3}$ и $\tfrac{4\pi}{3}$, максимум в $\tfrac{5\pi}{6}$ (на $y=1$), минимум в $\tfrac{11\pi}{6}$ (на $y=-1$).
3. Соедините плавной синусоидой: от нуля поднимитесь до максимума, опуститесь до следующего нуля, дальше — до минимума и назад к оси.
4. Продолжите периодически с шагом $2\pi$ влево/вправо.

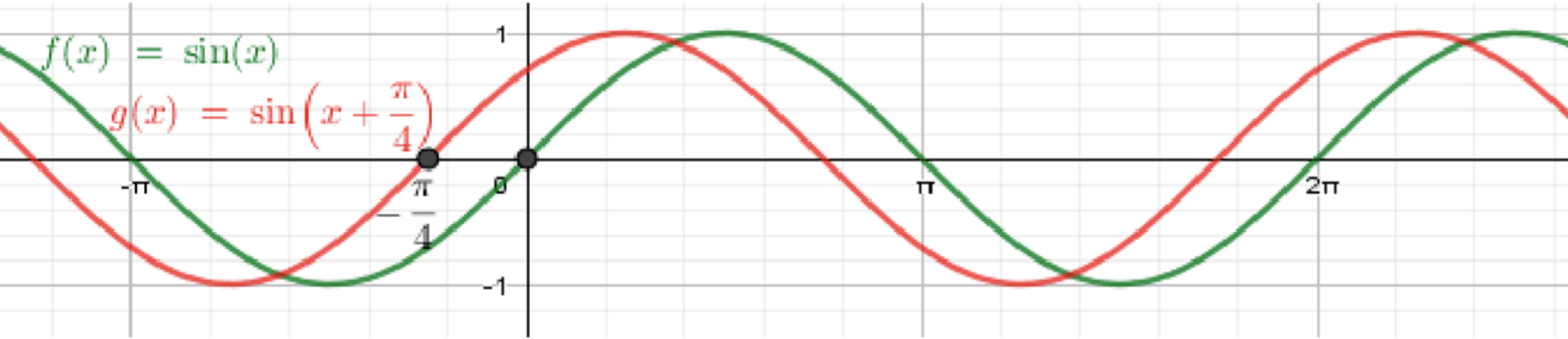
б) $y=\sin\!\left(x+\tfrac{\pi}{4}\right)$

Сдвиг: влево на $s=\tfrac{\pi}{4}$.

Удобная шкала: кратные $\tfrac{\pi}{4}$.

Опорные точки:

$$\left(-\tfrac{\pi}{4},0\right),\ \left(\tfrac{\pi}{4},1\right),\ \left(\tfrac{3\pi}{4},0\right),\ \left(\tfrac{5\pi}{4},-1\right),\ \left(\tfrac{7\pi}{4},0\right).$$

Для $[0,2\pi]$ используйте с $\tfrac{\pi}{4}$ по $\tfrac{7\pi}{4}$.

Нули в $[0,2\pi]$: $x=\tfrac{3\pi}{4},\ \tfrac{7\pi}{4}$.
Максимум: $x=\tfrac{\pi}{4}$.
Минимум: $x=\tfrac{5\pi}{4}$.

Возрастание: $(0,\tfrac{\pi}{4})$ и $(\tfrac{5\pi}{4},2\pi)$.
Убывание: $(\tfrac{\pi}{4},\tfrac{5\pi}{4})$.

Как чертить:

1. По $x$ разметьте $0,\ \tfrac{\pi}{4},\ \tfrac{3\pi}{4},\ \tfrac{5\pi}{4},\ \tfrac{7\pi}{4},\ 2\pi$.
2. Точки: максимум $(\tfrac{\pi}{4},1)$, нули $\tfrac{3\pi}{4}$ и $\tfrac{7\pi}{4}$, минимум $(\tfrac{5\pi}{4},-1)$.
3. Плавно соединяйте, соблюдая четверть-периодную «дугу» между соседними опорными точками.
4. Продолжите периодичность с шагом $2\pi$.

в) $y=\sin(x-\pi)$

Два эквивалентных взгляда:

• Сдвиг: вправо на $\pi$;
• Или тождество: $\sin(x-\pi)=-\sin x$ — отражение графика $y=\sin x$ относительно оси $x$.

Удобная шкала: кратные $\tfrac{\pi}{2}$.

Опорные точки:

$$(0,0),\ \left(\tfrac{\pi}{2},-1\right),\ (\pi,0),\ \left(\tfrac{3\pi}{2},1\right),\ (2\pi,0).$$

Нули в $[0,2\pi]$: $x=0,\ \pi,\ 2\pi$.
Максимум: $x=\tfrac{3\pi}{2}$.
Минимум: $x=\tfrac{\pi}{2}$.

Возрастание: $(\tfrac{\pi}{2},\tfrac{3\pi}{2})$.
Убывание: $(0,\tfrac{\pi}{2})$ и $(\tfrac{3\pi}{2},2\pi)$.

Как чертить:

1. Поставьте нули в $0,\pi,2\pi$.
2. Отразите «стандартную» синусоиду: над $(\tfrac{\pi}{2})$ не максимум, а минимум $-1$; над $(\tfrac{3\pi}{2})$ — максимум $1$.
3. Соедините плавно, затем продолжайте периодичность.

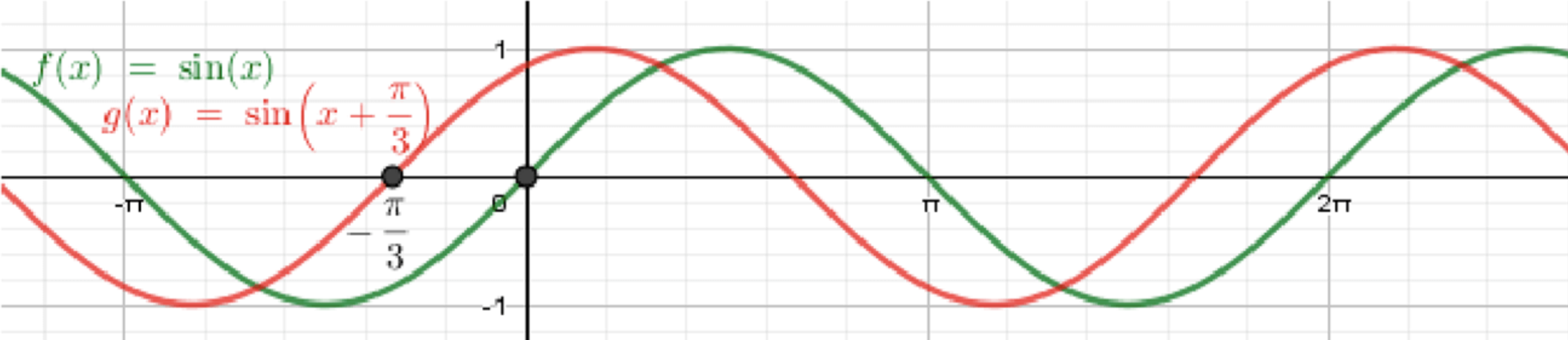
г) $y=\sin\!\left(x+\tfrac{\pi}{3}\right)$

Сдвиг: влево на $s=\tfrac{\pi}{3}$.

Удобная шкала: кратные $\tfrac{\pi}{6}$.

Опорные точки:

$$\left(-\tfrac{\pi}{3},0\right),\ \left(\tfrac{\pi}{6},1\right),\ \left(\tfrac{2\pi}{3},0\right),\ \left(\tfrac{7\pi}{6},-1\right),\ \left(\tfrac{5\pi}{3},0\right).$$

В $[0,2\pi]$ используйте со $\tfrac{\pi}{6}$ по $\tfrac{5\pi}{3}$.

Нули в $[0,2\pi]$: $x=\tfrac{2\pi}{3},\ \tfrac{5\pi}{3}$.
Максимум: $x=\tfrac{\pi}{6}$.
Минимум: $x=\tfrac{7\pi}{6}$.

Возрастание: $(0,\tfrac{\pi}{6})$ и $(\tfrac{7\pi}{6},2\pi)$.
Убывание: $(\tfrac{\pi}{6},\tfrac{7\pi}{6})$.

Как чертить:

1. Разметьте $0,\ \tfrac{\pi}{6},\ \tfrac{2\pi}{3},\ \tfrac{7\pi}{6},\ \tfrac{5\pi}{3},\ 2\pi$.
2. Отметьте максимум $(\tfrac{\pi}{6},1)$, нули $\tfrac{2\pi}{3},\tfrac{5\pi}{3}$, минимум $(\tfrac{7\pi}{6},-1)$.
3. Плавно соединяйте; далее продолжайте с периодом $2\pi$.