ГДЗ 10-11 Класс Номер 10.9 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \sin x — 2$;

б) $y = \sin x + 1$;

в) $y = \sin x + 2$;

г) $y = \sin x — 3$

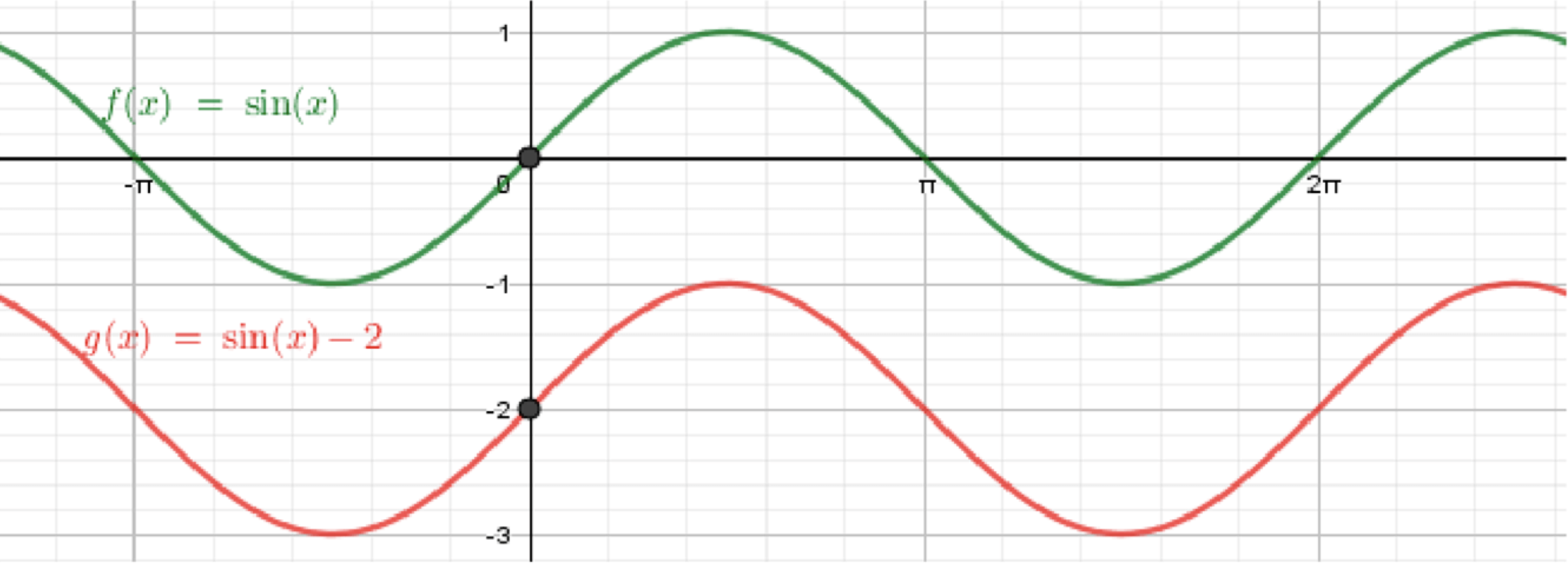
Построить график функции:

а) $y = \sin x — 2$;

Построим график функции $y = \sin x$;
Переместим его на 2 единицы вниз:

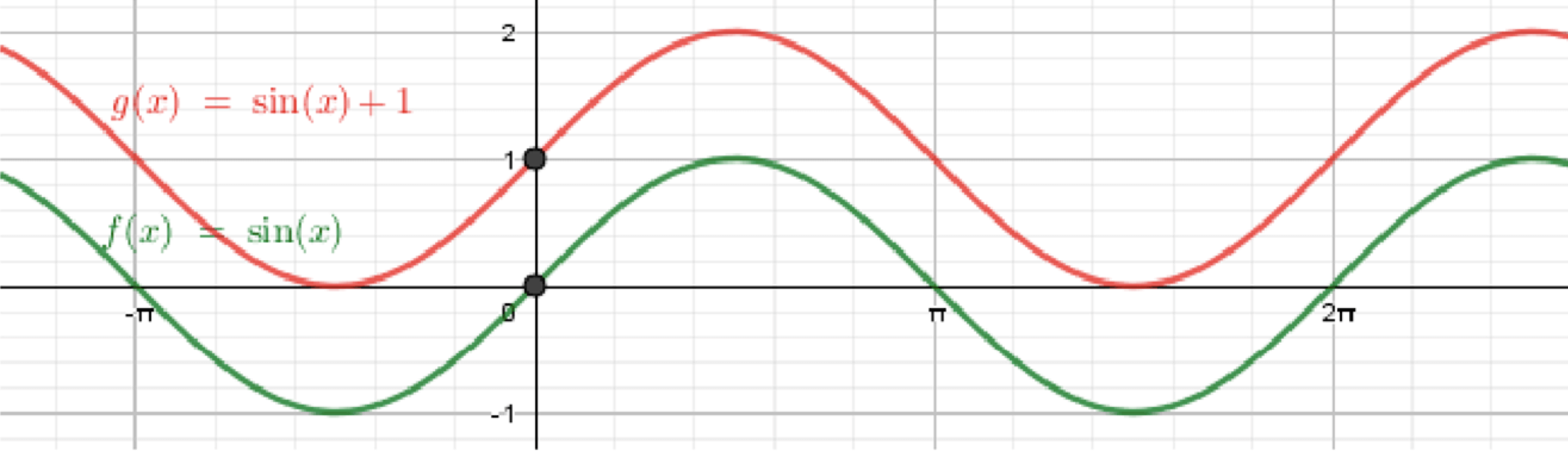
б) $y = \sin x + 1$;

Построим график функции $y = \sin x$;
Переместим его на 1 единицу вверх:

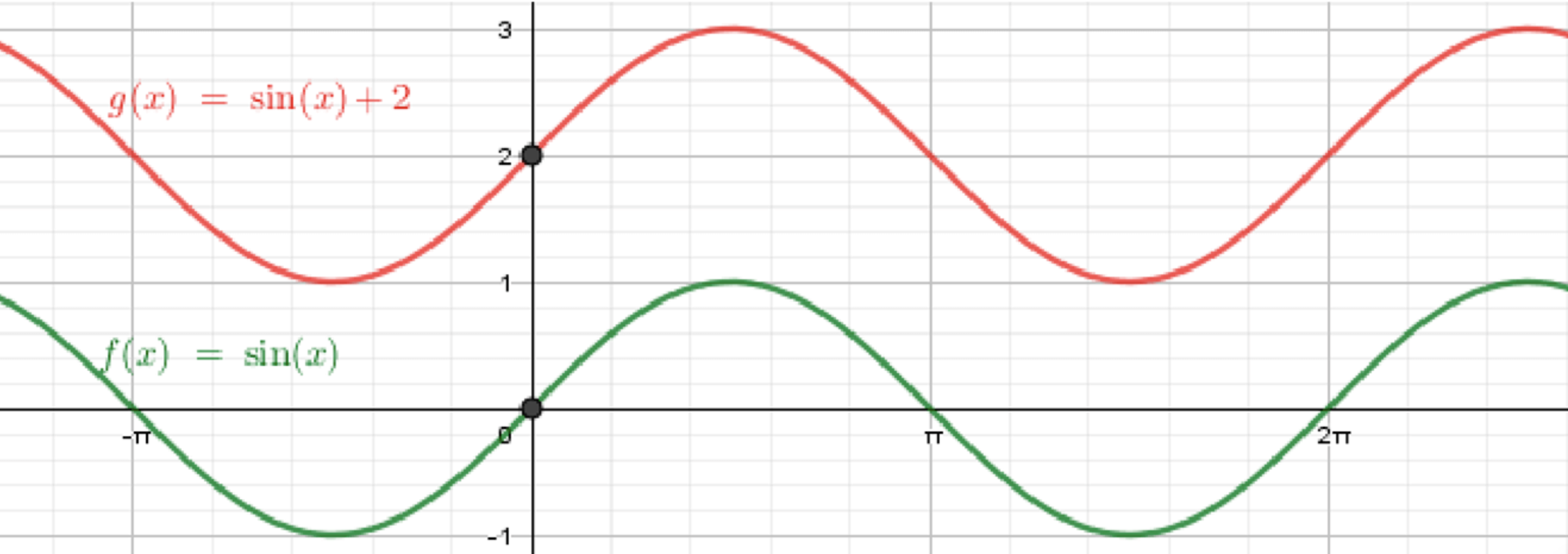
в) $y = \sin x + 2$;

Построим график функции $y = \sin x$;
Переместим его на 2 единицы вверх:

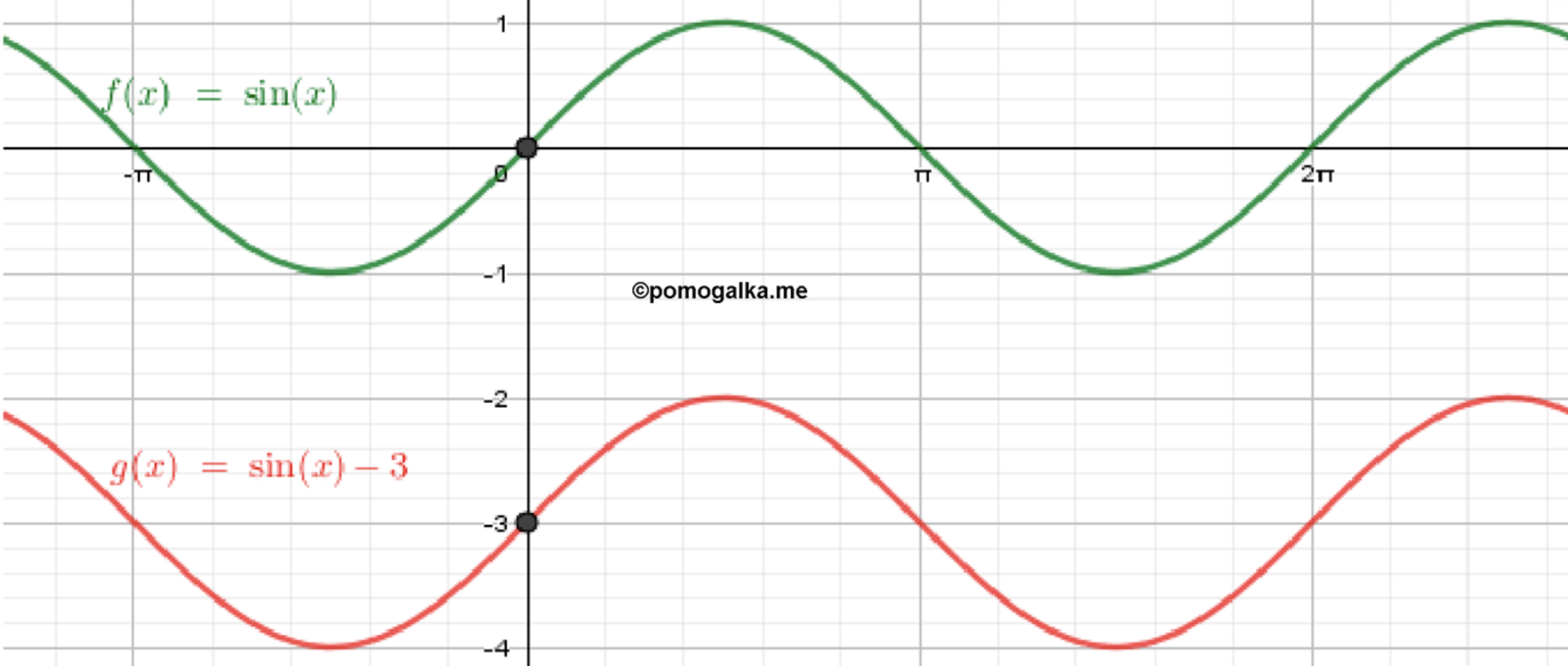
г) $y = \sin x — 3$;

Построим график функции $y = \sin x$;
Переместим его на 3 единицы вниз:

Общая схема для $y=\sin x + d$ (вертикальный сдвиг)

• Область определения: все $x\in\mathbb{R}$.
• Период: $2\pi$ (не меняется от $d$).
• Амплитуда: $1$ (не меняется от $d$).
• Средняя линия (ось колебаний): $y=d$.
• Диапазон значений: $[d-1,\; d+1]$.
• Максимумы: при $x=\tfrac{\pi}{2}+2\pi k$, значение $1+d$.
• Минимумы: при $x=\tfrac{3\pi}{2}+2\pi k$, значение $-1+d$.
• Пересечение с осью $Oy$: $(0,\; d)$.
• Нули (пересечения с $Ox$): решения $\sin x = -d$.
  ─ Если $|d|<1$ — нули есть (две точки на период).
  ─ Если $|d|=1$ — график касается $Ox$ в мини- или макс-точках.
  ─ Если $|d|>1$ — нулей нет.
• Производная/монотонность: $y’=\cos x$.
  Возрастает на $\big(-\tfrac{\pi}{2}+2\pi k,\ \tfrac{\pi}{2}+2\pi k\big)$, убывает на $\big(\tfrac{\pi}{2}+2\pi k,\ \tfrac{3\pi}{2}+2\pi k\big)$.
• Выпуклость: $y»=-\sin x$.
  Вниз на $(0+2\pi k,\ \pi+2\pi k)$, вверх на $(\pi+2\pi k,\ 2\pi+2\pi k)$.
• Пять «опорных» точек за период (например, от $0$ до $2\pi$):

  $$(0,\ d),\quad \Big(\tfrac{\pi}{2},\ 1+d\Big),\quad (\pi,\ d),\quad \Big(\tfrac{3\pi}{2},\ -1+d\Big),\quad (2\pi,\ d).$$

• Как чертить вообще:
  1. Проведите горизонтальную линию $y=d$ — это «середина волны».
  2. От неё отметьте по вертикали уровни $y=d+1$ (вершины) и $y=d-1$ (впадины).
  3. По оси $x$ разметьте точки $0,\ \tfrac{\pi}{2},\ \pi,\ \tfrac{3\pi}{2},\ 2\pi$ (и далее с шагом $2\pi$).
  4. Поставьте опорные точки, соедините их плавной синусоидой; повторяйте с периодом $2\pi$.
  5. Проверьте: значение в $x=0$ равно $d$; вершина действительно на $\tfrac{\pi}{2}$, впадина — на $\tfrac{3\pi}{2}$.

а) $y=\sin x — 2$ $(d=-2)$

Параметры. Период $2\pi$, амплитуда $1$, средняя линия $y=-2$, диапазон $[-3,-1]$.

Ключевые уровни: вершины $y=-1$, впадины $y=-3$.

Опорные точки за $[0,2\pi]$:

$$(0,-2),\quad \Big(\tfrac{\pi}{2},-1\Big),\quad (\pi,-2),\quad \Big(\tfrac{3\pi}{2},-3\Big),\quad (2\pi,-2).$$

Экстремумы (все $k\in\mathbb{Z}$)

• максимумы: $x=\tfrac{\pi}{2}+2\pi k,\ y=-1$;
• минимумы: $x=\tfrac{3\pi}{2}+2\pi k,\ y=-3$.

Нули: $\sin x-2=0 \iff \sin x=2$ — нет решений ($|2|>1$), пересечений с $Ox$ нет; весь график ниже оси $Ox$.

Монотонность (как у $\sin x$):
возрастает на $\big(-\tfrac{\pi}{2}+2\pi k,\ \tfrac{\pi}{2}+2\pi k\big)$, убывает на $\big(\tfrac{\pi}{2}+2\pi k,\ \tfrac{3\pi}{2}+2\pi k\big)$.

Как построить:

1. Проведите линию $y=-2$.
2. Проведите уровни $y=-1$ и $y=-3$.
3. Отметьте $x=0,\tfrac{\pi}{2},\pi,\tfrac{3\pi}{2},2\pi$; поставьте опорные точки, как выше.
4. Соедините плавной волной; продлите с периодом $2\pi$.

б) $y=\sin x + 1$ $(d=+1)$

Параметры. Средняя линия $y=1$, диапазон $[0,2]$.

Ключевые уровни: вершины $y=2$, впадины $y=0$.

Опорные точки за $[0,2\pi]$:

$$(0,1),\quad \Big(\tfrac{\pi}{2},2\Big),\quad (\pi,1),\quad \Big(\tfrac{3\pi}{2},0\Big),\quad (2\pi,1).$$

Экстремумы:

• максимумы: $x=\tfrac{\pi}{2}+2\pi k,\ y=2$;
• минимумы: $x=\tfrac{3\pi}{2}+2\pi k,\ y=0$.

Нули: $\sin x + 1=0 \iff \sin x=-1$.
Решения: $x=\tfrac{3\pi}{2}+2\pi k$ (или $-\tfrac{\pi}{2}+2\pi k$).
Здесь график касается оси $Ox$ в точках минимума (касательная горизонтальна).

Монотонность: как у $\sin x$.

Как построить:

1. Линия $y=1$, уровни $y=0$ и $y=2$.
2. Разметьте стандартные $x$-точки, поставьте опорные точки.
3. Соедините плавной кривой; отметьте касание $Ox$ в $x=\tfrac{3\pi}{2}+2\pi k$.

в) $y=\sin x + 2$ $(d=+2)$

Параметры. Средняя линия $y=2$, диапазон $[1,3]$.

Ключевые уровни: вершины $y=3$, впадины $y=1$.

Опорные точки за $[0,2\pi]$:

$$(0,2),\quad \Big(\tfrac{\pi}{2},3\Big),\quad (\pi,2),\quad \Big(\tfrac{3\pi}{2},1\Big),\quad (2\pi,2).$$

Экстремумы:

• максимумы: $x=\tfrac{\pi}{2}+2\pi k,\ y=3$;
• минимумы: $x=\tfrac{3\pi}{2}+2\pi k,\ y=1$.

Нули: $\sin x+2=0 \iff \sin x=-2$ — нет решений ($|-2|>1$). Весь график выше оси $Ox$.

Монотонность: как у $\sin x$.

Как построить:

1. Линия $y=2$, уровни $y=1$ и $y=3$.
2. Отметьте стандартные $x$-точки, поставьте опорные.
3. Соедините плавной синусоидой; продлите с периодом.

г) $y=\sin x — 3$ $(d=-3)$

Параметры. Средняя линия $y=-3$, диапазон $[-4,-2]$.

Ключевые уровни: вершины $y=-2$, впадины $y=-4$.

Опорные точки за $[0,2\pi]$:

$$(0,-3),\quad \Big(\tfrac{\pi}{2},-2\Big),\quad (\pi,-3),\quad \Big(\tfrac{3\pi}{2},-4\Big),\quad (2\pi,-3).$$

Экстремумы:

• максимумы: $x=\tfrac{\pi}{2}+2\pi k,\ y=-2$;
• минимумы: $x=\tfrac{3\pi}{2}+2\pi k,\ y=-4$.

Нули: $\sin x-3=0 \iff \sin x=3$ — нет решений. Весь график ниже оси $Ox$.

Монотонность: как у $\sin x$.

Как построить:

1. Линия $y=-3$, уровни $y=-2$ и $y=-4$.
2. Разметьте стандартные $x$-точки, поставьте опорные.
3. Соедините плавной синусоидой и продлите периодически.