Краткий ответ:
Решить графически уравнение:
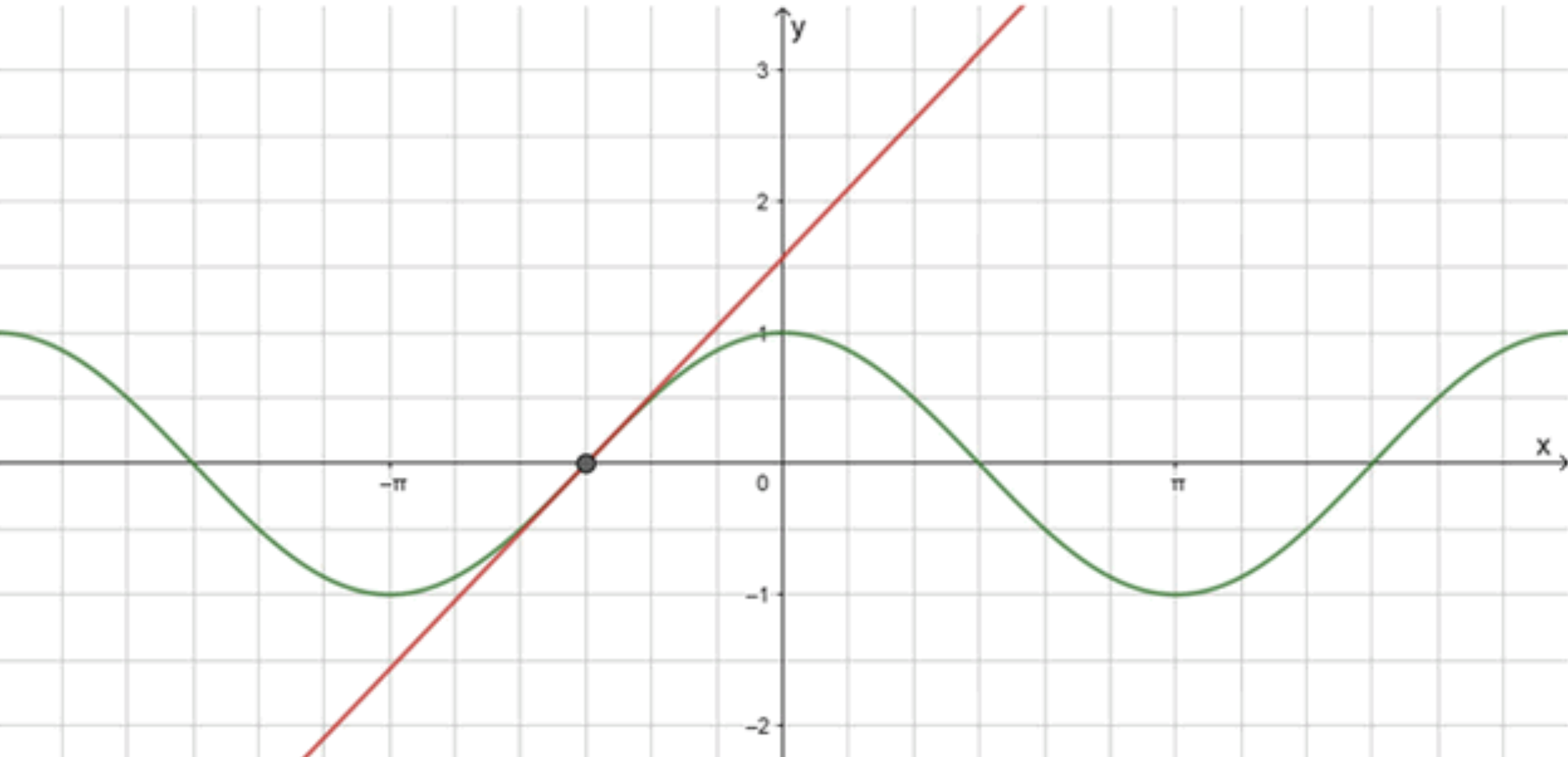
а) cos x = x + π 2 \cos x = x + \frac{\pi}{2}
y = cos x y = \cos x
y = x + π 2 y = x + \frac{\pi}{2}
x x
− π 2 -\frac{\pi}{2} 0 0 y y 0 0 ≈ 1 , 5 \approx 1,5
Графики функций:
Ответ: x = − π 2 x = -\frac{\pi}{2}
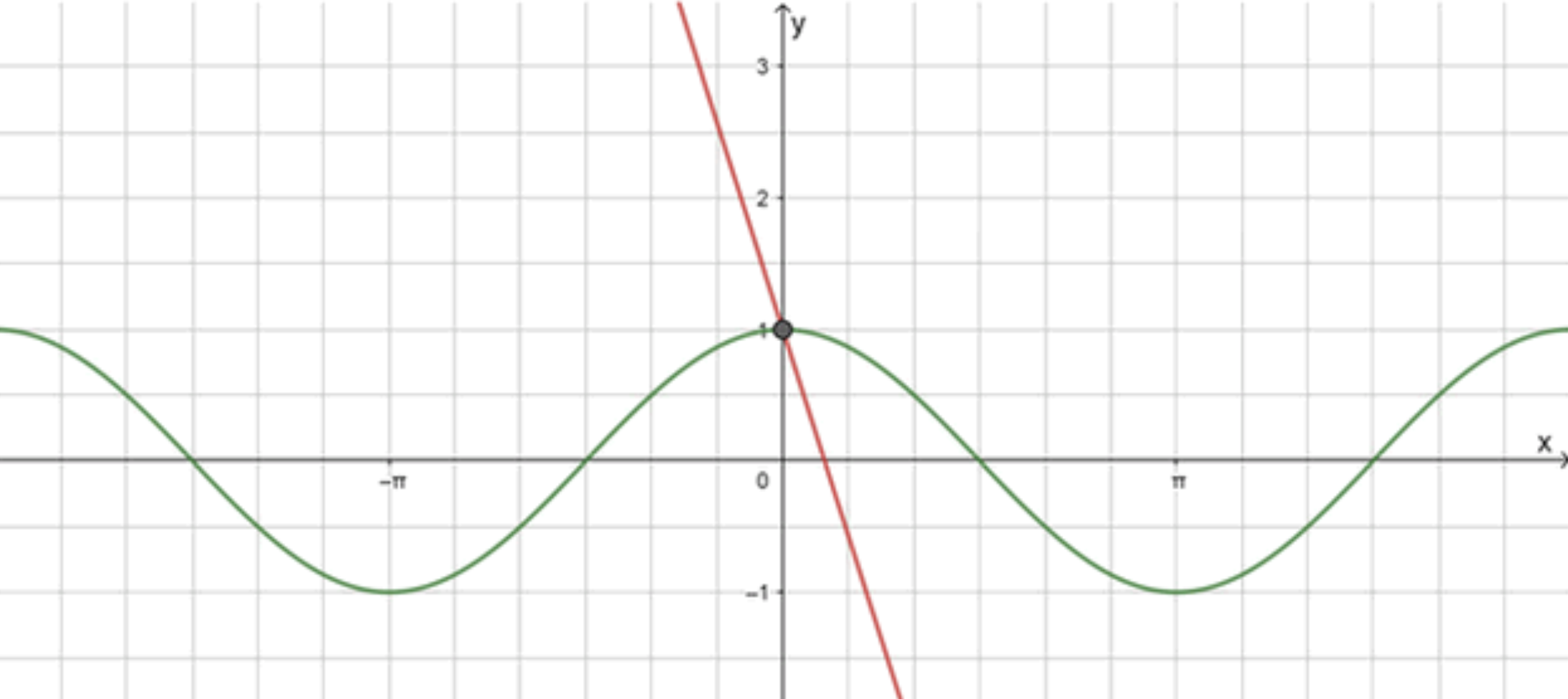
б) − cos x = 3 x − 1 -\cos x = 3x — 1 cos x = 1 − 3 x \cos x = 1 — 3x
y = cos x y = \cos x
y = 1 − 3 x y = 1 — 3x
Графики функций:
Ответ: x = 0 x = 0
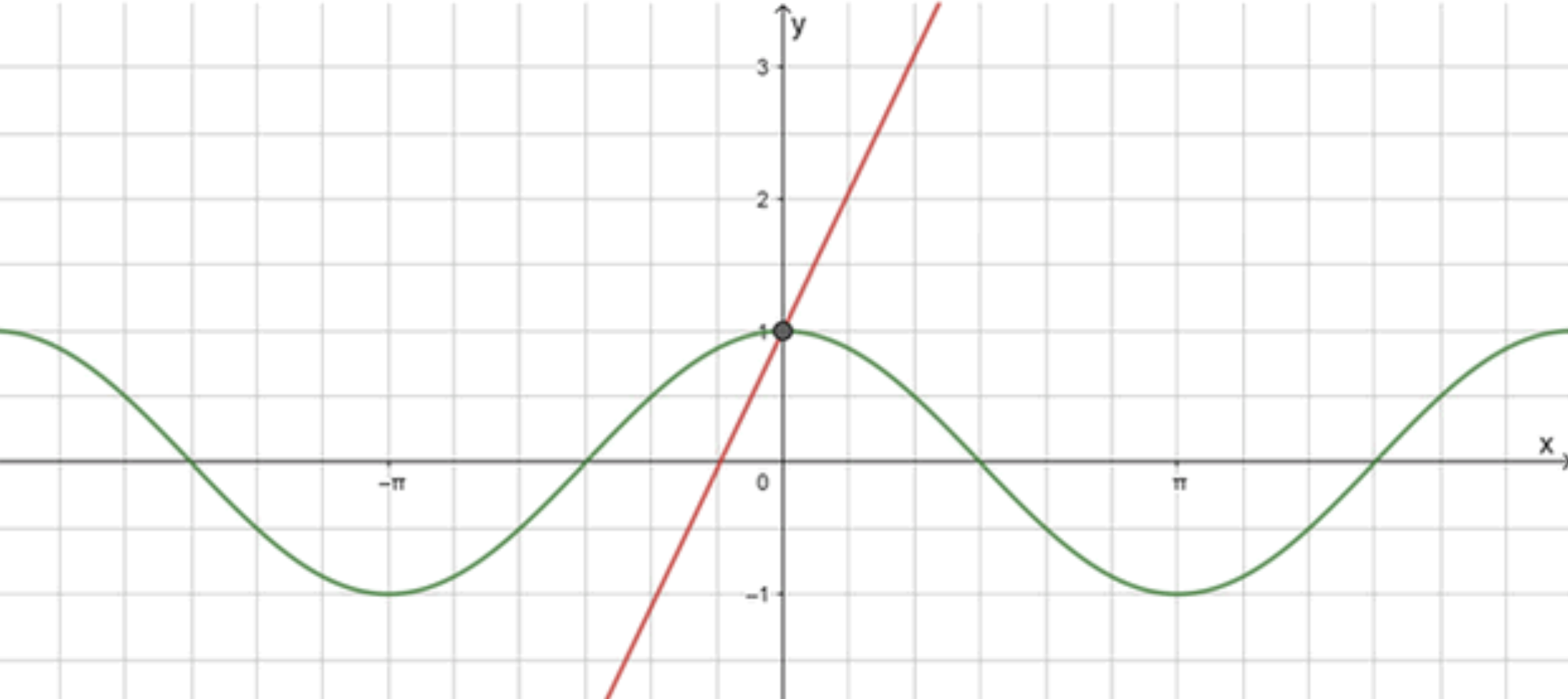
в) cos x = 2 x + 1 \cos x = 2x + 1
y = cos x y = \cos x
y = 2 x + 1 y = 2x + 1
Графики функций:
Ответ: x = 0 x = 0
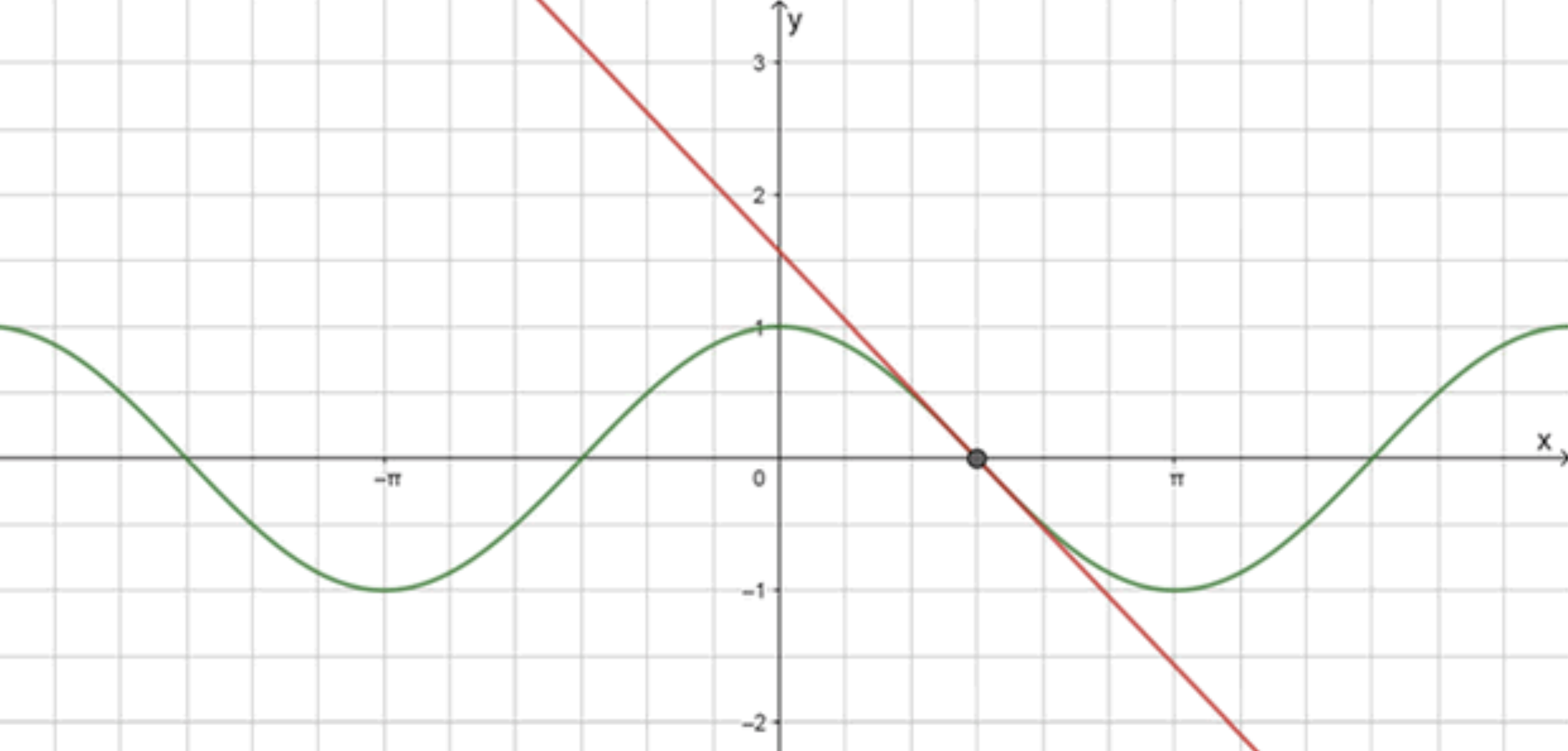
г) cos x = − x + π 2 \cos x = -x + \frac{\pi}{2}
y = cos x y = \cos x
y = − x + π 2 y = -x + \frac{\pi}{2}
x x
0 0 π 2 \frac{\pi}{2} y y ≈ 1 , 5 \approx 1,5 0 0
Графики функций:
Ответ: x = π 2 x = \frac{\pi}{2}
Подробный ответ:
а) cos x = x + π 2 \cos x = x+\dfrac{\pi}{2}
1) Сведение к нулю функции
h ( x ) = cos x − x − π 2 h(x)=\cos x — x — \dfrac{\pi}{2} h ( x ) = 0 h(x)=0
2) Локализация корня по диапазону значений
Так как ∣ cos x ∣ ≤ 1 |\cos x|\le 1 x + π 2 ∈ [ − 1 , 1 ] x+\dfrac{\pi}{2}\in[-1,1]
− 1 ≤ x + π 2 ≤ 1 ⟹
x ∈ [ − 1 − π 2 , 1 − π 2 ] ≈ [ − 2,571 , − 0,571 ] . -1\le x+\frac{\pi}{2}\le 1 \ \Longrightarrow\ x\in\Big[-1-\frac{\pi}{2},\ 1-\frac{\pi}{2}\Big]\approx[-2{,}571,\,-0{,}571].
3) Единственность (монотонность h h
h ′ ( x ) = − sin x − 1 ∈ [ − 2 , 0 ] h'(x)=-\sin x-1\in[-2,0] x x h h строго убывает (кроме изолированных точек со h ′ = 0 h’=0 не более одного корня.
4) Нахождение корня и проверка
Подставляем x = − π 2 x=-\dfrac{\pi}{2} cos ( − π 2 ) = 0 \cos(-\tfrac{\pi}{2})=0 − π 2 + π 2 = 0 -\tfrac{\pi}{2}+\tfrac{\pi}{2}=0
x = − π 2 (единственный корень), y = 0. \boxed{x=-\frac{\pi}{2}} \quad\text{(единственный корень),}\quad y=0.
б) − cos x = 3 x − 1 -\cos x = 3x-1 ⇒ \Rightarrow cos x = 1 − 3 x \cos x = 1-3x
1) Сведение
h ( x ) = cos x − ( 1 − 3 x ) = cos x − 1 + 3 x h(x)=\cos x — (1-3x)=\cos x -1 +3x
2) Локализация
Требуем 1 − 3 x ∈ [ − 1 , 1 ] ⇒ − 1 ≤ 1 − 3 x ≤ 1 ⇒ 0 ≤ x ≤ 2 3 1-3x\in[-1,1]\Rightarrow -1\le 1-3x\le 1 \Rightarrow 0\le x\le \tfrac{2}{3}
3) Единственность
h ′ ( x ) = − sin x + 3 ∈ [ 2 , 4 ] ⇒ h h'(x)=-\sin x+3\in[2,4]\Rightarrow h строго возрастает ⇒ \Rightarrow единственный .
4) Корень и проверка
x = 0 : cos 0 = 1 , 1 − 3 ⋅ 0 = 1 x=0:\ \cos 0=1,\ 1-3\cdot 0=1
x = 0 (единственный корень), y = 1. \boxed{x=0}\quad\text{(единственный корень),}\quad y=1.
в) cos x = 2 x + 1 \cos x = 2x+1
1) Сведение
h ( x ) = cos x − 2 x − 1 h(x)=\cos x -2x -1
2) Локализация
2 x + 1 ∈ [ − 1 , 1 ] ⇒ − 2 ≤ 2 x ≤ 0 ⇒ − 1 ≤ x ≤ 0 2x+1\in[-1,1]\Rightarrow -2\le 2x\le 0\Rightarrow -1\le x\le 0
3) Единственность
h ′ ( x ) = − sin x − 2 ∈ [ − 3 , − 1 ] < 0 ⇒ h h'(x)=-\sin x-2\in[-3,-1]<0\Rightarrow h строго убывает ⇒ \Rightarrow единственный .
4) Корень и проверка
x = 0 : cos 0 = 1 , 2 ⋅ 0 + 1 = 1 x=0:\ \cos 0=1,\ 2\cdot 0+1=1
x = 0 (единственный корень), y = 1. \boxed{x=0}\quad\text{(единственный корень),}\quad y=1.
г) cos x = − x + π 2 \cos x = -x+\dfrac{\pi}{2}
1) Сведение
h ( x ) = cos x + x − π 2 h(x)=\cos x + x — \dfrac{\pi}{2}
2) Локализация
− x + π 2 ∈ [ − 1 , 1 ] ⇒ x ∈ [ π 2 − 1 , π 2 + 1 ] ≈ [ 0,571 , 2,571 ] . -x+\dfrac{\pi}{2}\in[-1,1]\Rightarrow x\in\Big[\frac{\pi}{2}-1,\ \frac{\pi}{2}+1\Big]\approx[0{,}571,\ 2{,}571].
3) Единственность
h ′ ( x ) = − sin x + 1 ∈ [ 0 , 2 ] h'(x)=-\sin x+1\in[0,2] h h неубывает и, кроме изолированных точек x = π 2 + 2 π k x=\tfrac{\pi}{2}+2\pi k h ′ = 0 h’=0 не более одного .
4) Корень и проверка
x = π 2 : cos ( π 2 ) = 0 , − π 2 + π 2 = 0 x=\dfrac{\pi}{2}:\ \cos(\tfrac{\pi}{2})=0,\ -\tfrac{\pi}{2}+\tfrac{\pi}{2}=0
x = π 2 (единственный корень), y = 0. \boxed{x=\frac{\pi}{2}}\quad\text{(единственный корень),}\quad y=0.