Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 11.12 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Решите графически уравнение:
а) ;
б) ;
в) ;
г)
Решить графически уравнение:
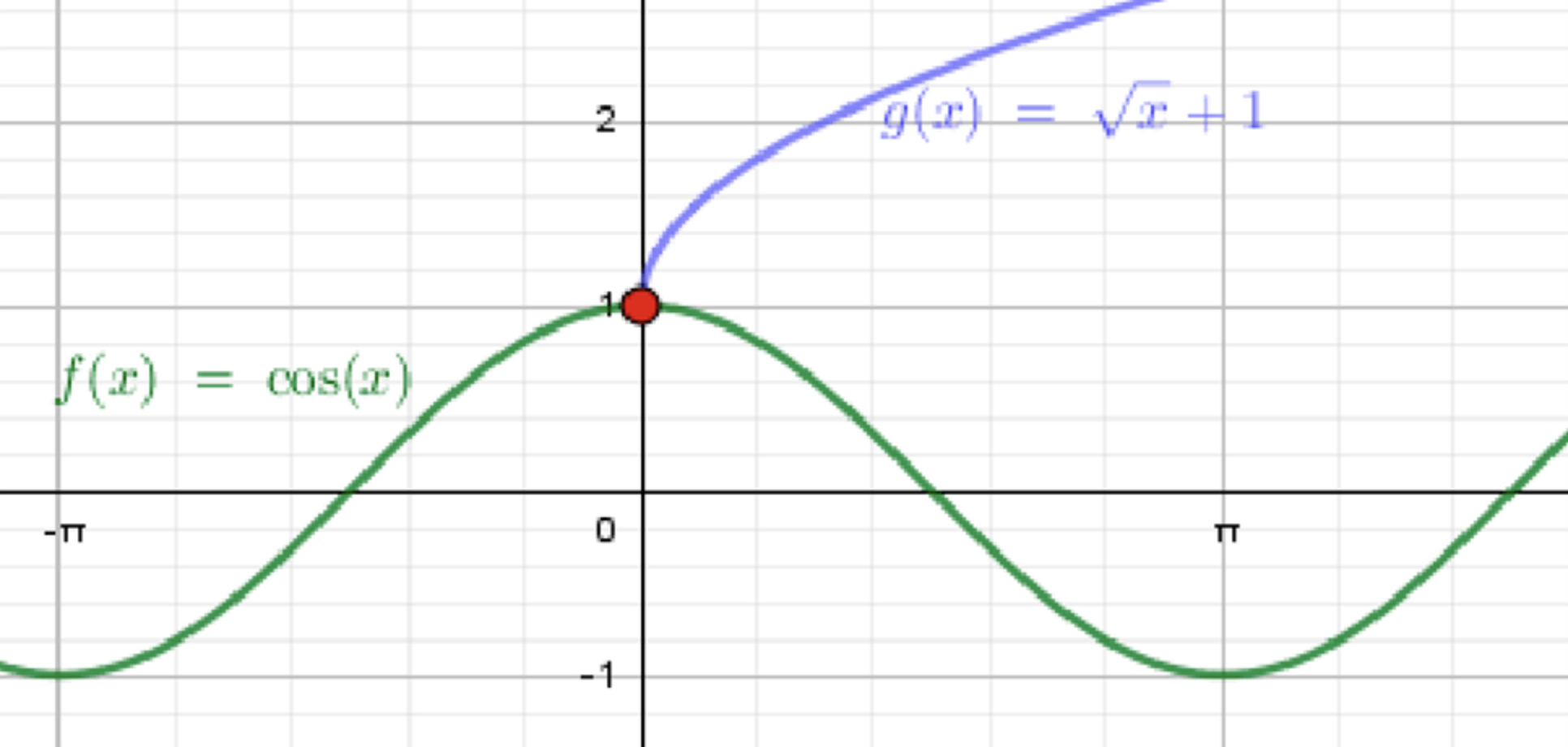
а) ;
— уравнение синусоиды;
— ветвь параболы:
;
| 0 | 1 | |
|---|---|---|
| 1 | 2 |
Графики функций:
Ответ: .
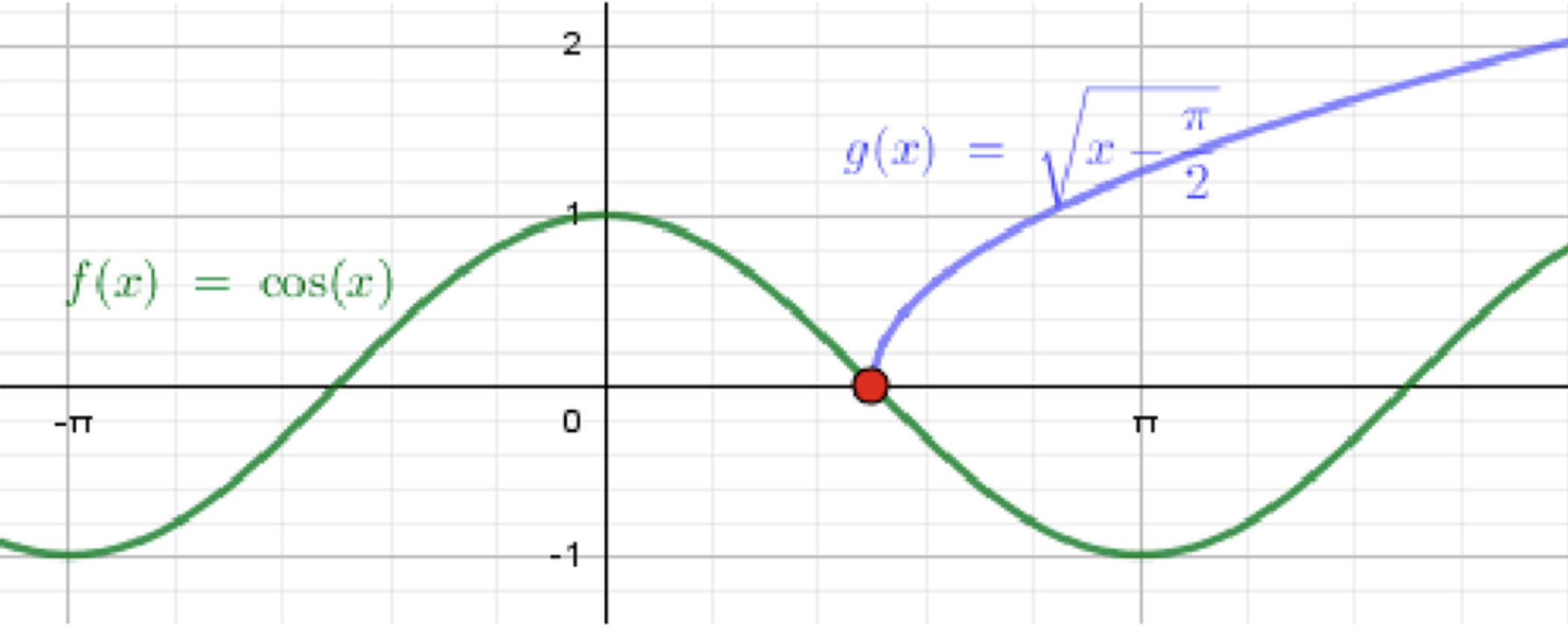
б) ;
— уравнение синусоиды;
— ветвь параболы:
;
| 0 | ≈ 1 |
Графики функций:
Ответ: .
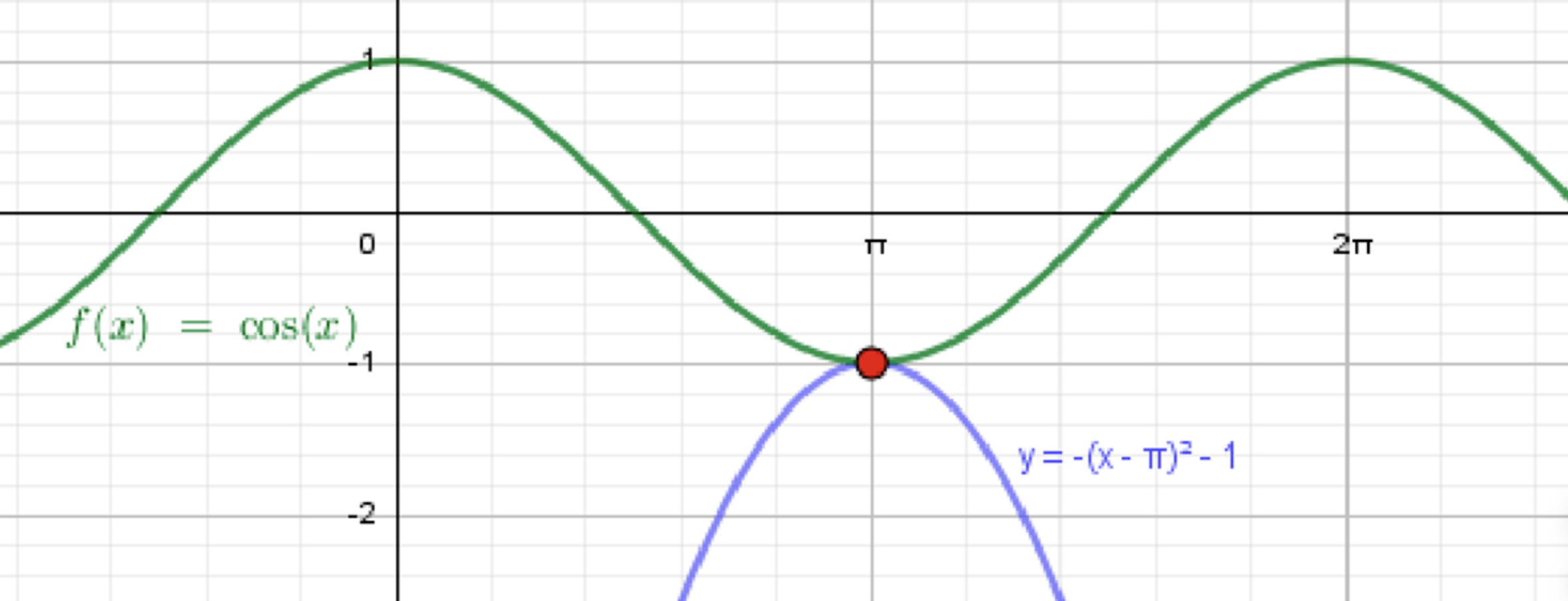
в) ;
— уравнение синусоиды;
— уравнение параболы:
;
| ≈ -2 | -1 | ≈ -2 |
Графики функций:
Ответ: .
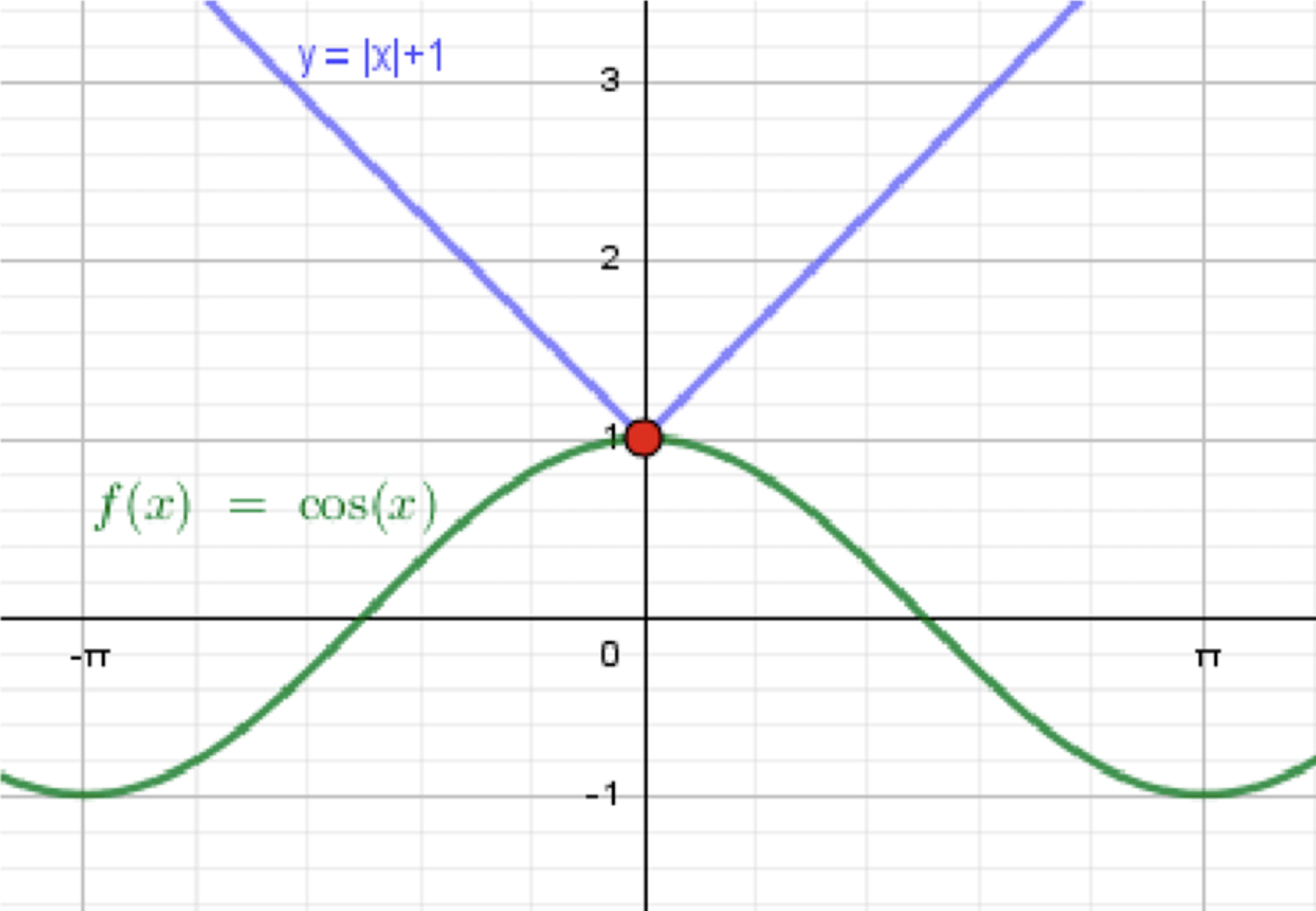
г) ;
— уравнение синусоиды;
— уравнение ломаной:
;
| -1 | 0 | 1 | |
|---|---|---|---|
| 2 | 1 | 2 |
Графики функций:
Ответ: .
а)
Область: правая часть определена при .
Ключевое наблюдение: для всех , причём .
А и только при .
Разбор случаев.
- Если : — решение.
- Если : , а ⇒ равенство невозможно.
- Если : , а (и равен 1 только при , где всё равно ) ⇒ равенство невозможно.
Вывод: единственный корень (и ).
б)
Область: . Правая часть .
Знак левой части:
- На имеем ⇒ с совпасть не может.
- В точке : — кандидат на решение.
- Для : , а ⇒ равенство невозможно.
Вывод: — единственное решение (и ).
в)
Оценки сторон: для любого ,
Равенство возможно только, если обе стороны равны .
- Правая сторона ⇔ ⇔ .
- Левая ⇔ , .
Совместно даёт .
Вывод: — единственный корень (и ).
г)
Оценки: (равно только при ); (равно при ).
- Если : ⇒ равенство невозможно.
- Если : — решение.
Вывод: — единственный корень (и ).