Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 11.13 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Сколько решений имеет система уравнений:
а)
б)
в)
г)
Найти количество решений системы уравнений:
а)
— уравнение синусоиды;
— уравнение параболы:
| 0 | 1 | 2 | |
|---|---|---|---|
| -3 | -2 | -3 |
Графики функций:
Ответ: нет решений.
б)
— уравнение синусоиды;
— уравнение гиперболы:
| 1 | 2 | |
|---|---|---|
| 2 | 1 |
Графики функций:
Ответ: бесконечно много решений.
в)
— уравнение синусоиды;
— уравнение параболы:
| -1 | 0 | 1 | |
|---|---|---|---|
| -2 | -3 | -2 |
Графики функций:
Ответ: 2 решения.
г)
— уравнение синусоиды;
— уравнение ломаной:
| -1 | 0 | 1 | |
|---|---|---|---|
| 1 | 0 | 1 |
Графики функций:
Ответ: 2 решения.
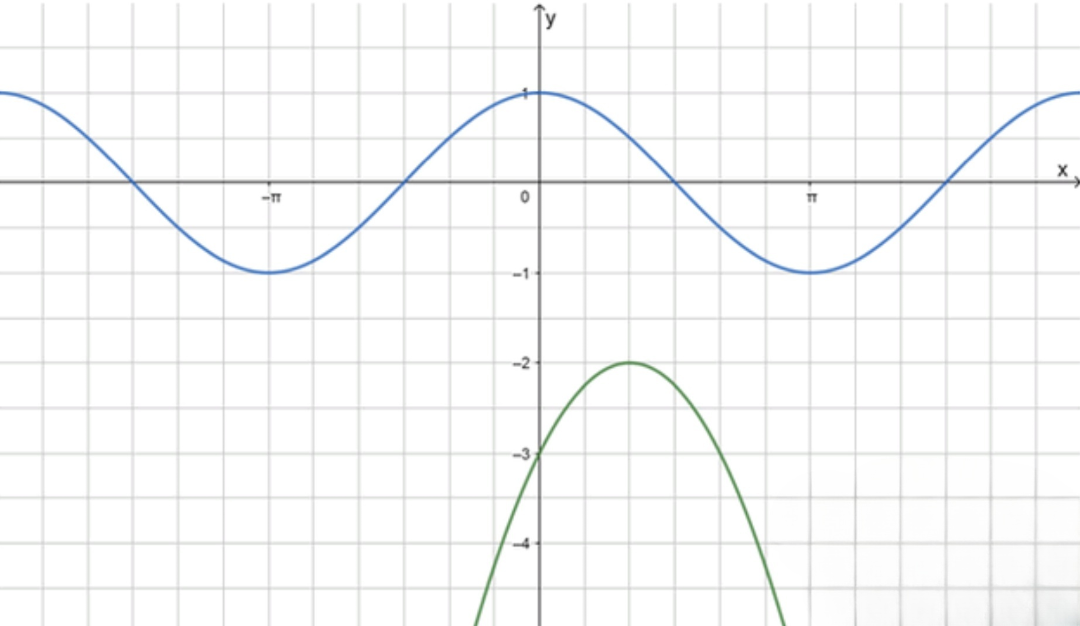
а)
Идея. Сравним диапазоны значений.
Парабола:
Максимум равен и достигается при .
Косинус принимает значения только из .
Так как для любого значение параболы , равенство невозможно.
Вывод: решений нет.
(Для полноты: уравнение даёт с , что тоже подтверждает отсутствие пересечений.)
График:
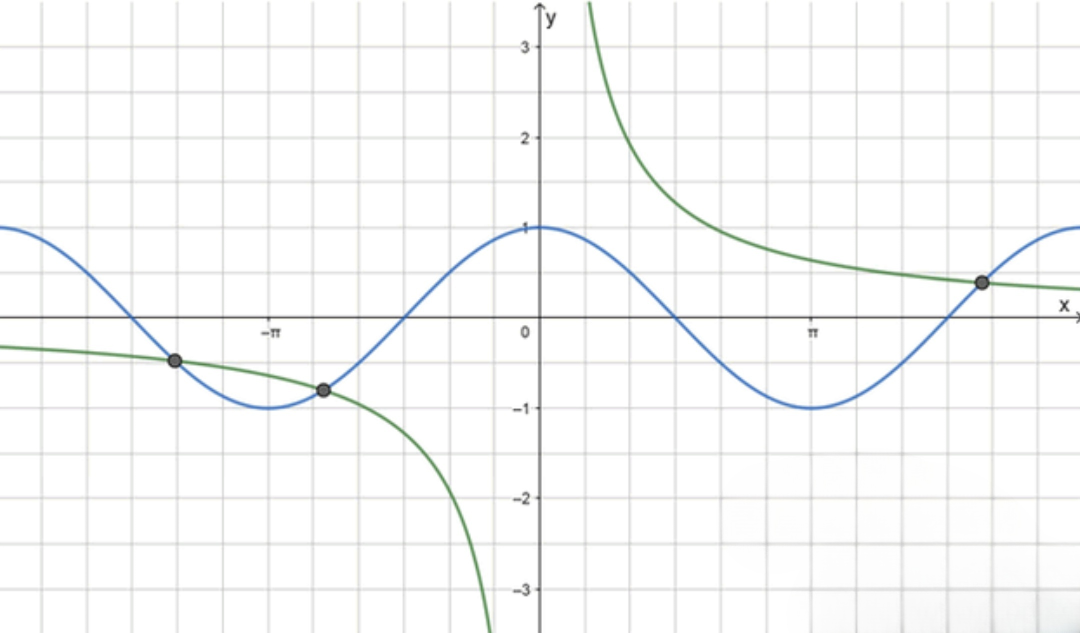
б)
Эквивалентно: (при ).
1) Где решений точно нет.
- При : , а ⇒ равенство невозможно.
- При : , а ⇒ тоже невозможно.
- В точках : ⇒ тоже не решения.
2) Почему решений бесконечно много.
Рассмотрим функцию , непрерывную на .
Для каждого :
По теореме о промежуточных значениях на каждом отрезке есть хотя бы один корень. Аналогично на . Следовательно, для всех достаточно больших — минимум по одному корню на каждую полупериодную дугу, значит корней бесконечно много (и справа, и слева по оси).
Вывод: решений бесконечно много.
(Численно первые корни: — см. таблицу.)
График:
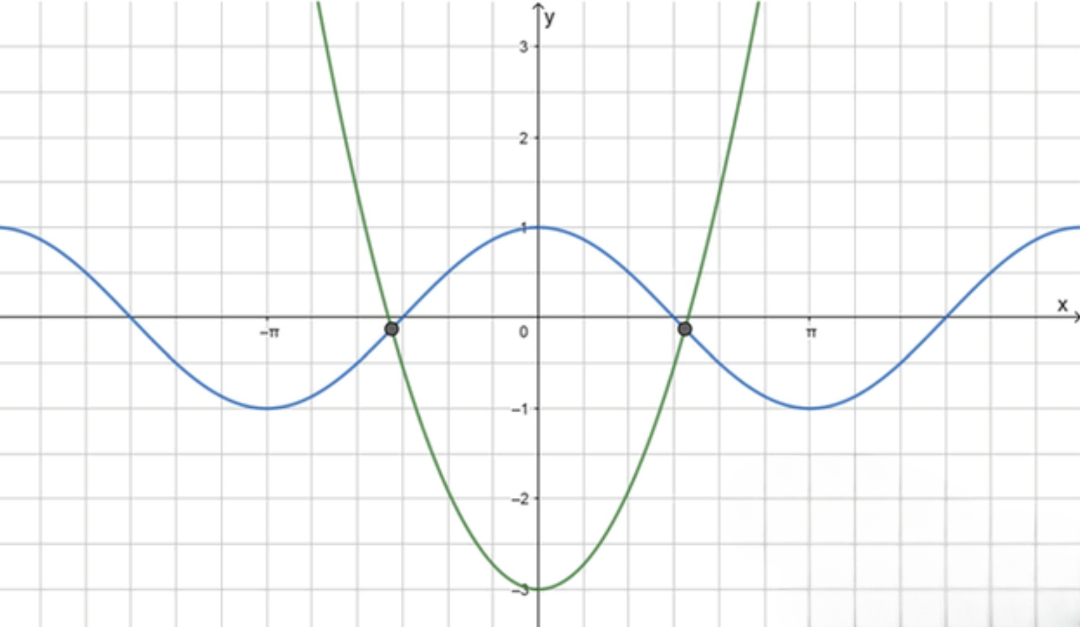
в)
Эквивалентно: .
1) Возможные по диапазону значений.
Нужно, чтобы . Решая
Вне этих промежутков правая часть или , а , поэтому решений там нет.
2) Ровно по одному корню на каждом промежутке.
Рассмотрим .
- На :
К тому же , т.е. строго убывает ⇒ ровно один корень.
- На :
а ⇒ строго возрастает ⇒ ровно один корень.
Вывод: всего решения (симметричные по знаку).
Численно: .
График:
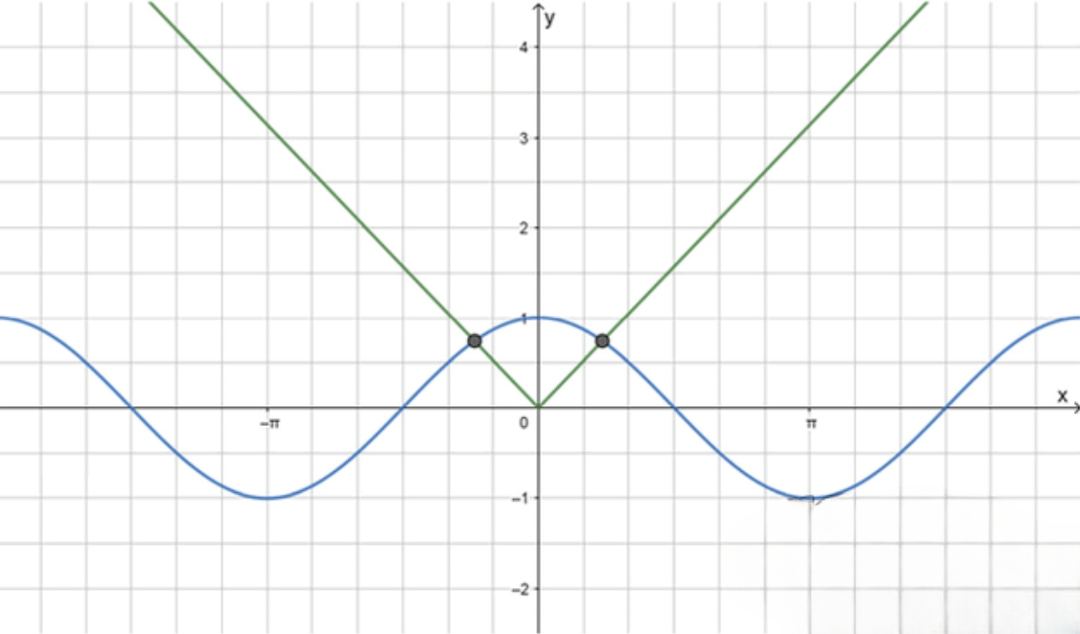
г)
Эквивалентно: .
1) Ограничения.
Так как и , обязательно и . Значит, ищем решения в , где .
2) Сведение к двух задачам на .
По симметрии :
- для получаем ;
- для получаем , то есть при .
Функция на : , , ⇒ ровно один корень (так называемое «число Дотти» ). Второе решение — .
Вывод: решения: .
График: