ГДЗ 10-11 Класс Номер 11.5 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Построить график функции:

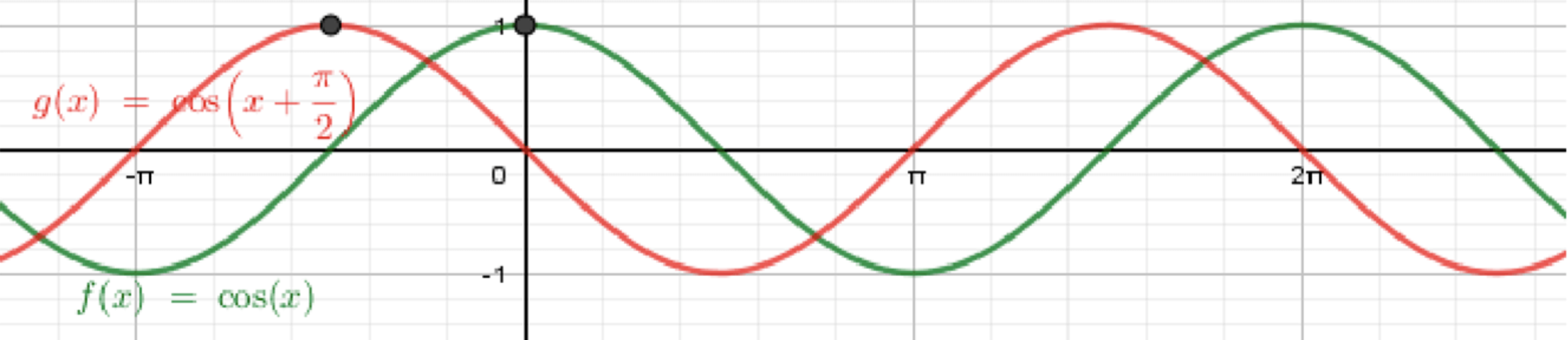
а) $y = \cos\left(x + \frac{\pi}{2}\right);$

Построим график функции $y = \cos x;$

Переместим его на $\frac{\pi}{2}$ единиц влево:

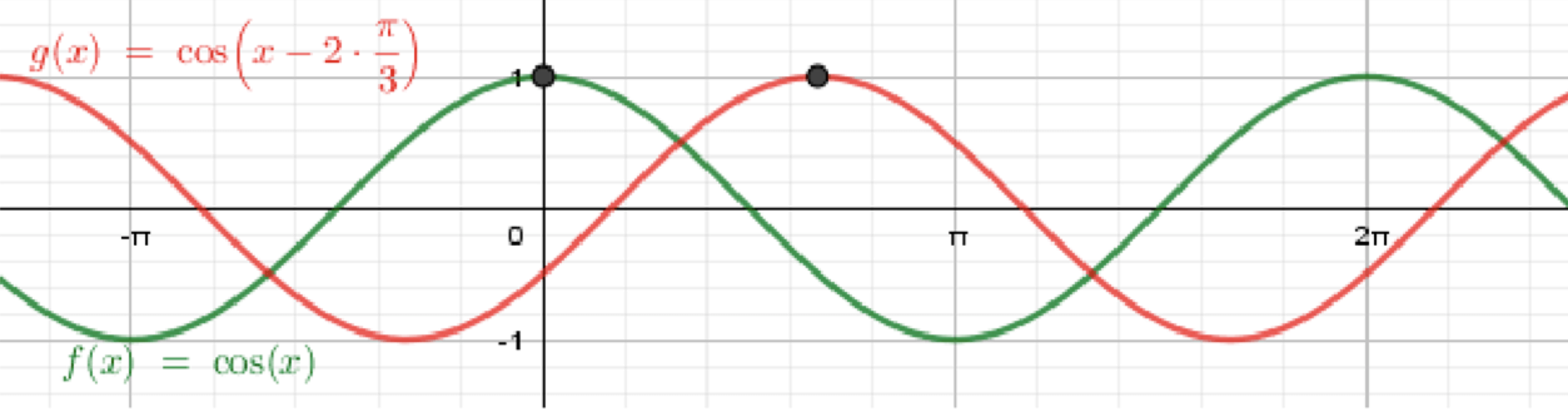
б) $y = \cos\left(x — \frac{2\pi}{3}\right);$

Построим график функции $y = \cos x;$

Переместим его на $\frac{2\pi}{3}$ единиц вправо:

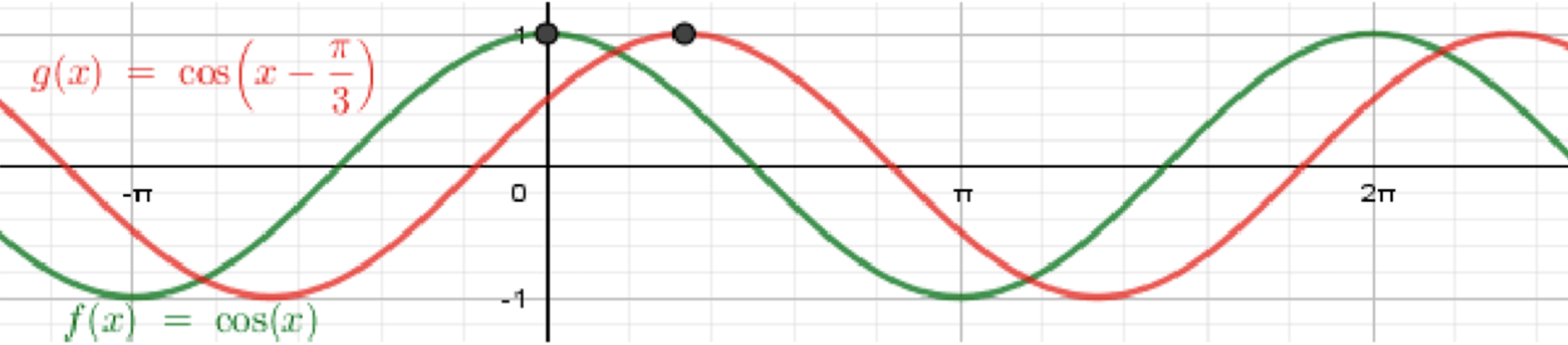
в) $y = \cos\left(x — \frac{\pi}{3}\right);$

Построим график функции $y = \cos x;$

Переместим его на $\frac{\pi}{3}$ единиц вправо:

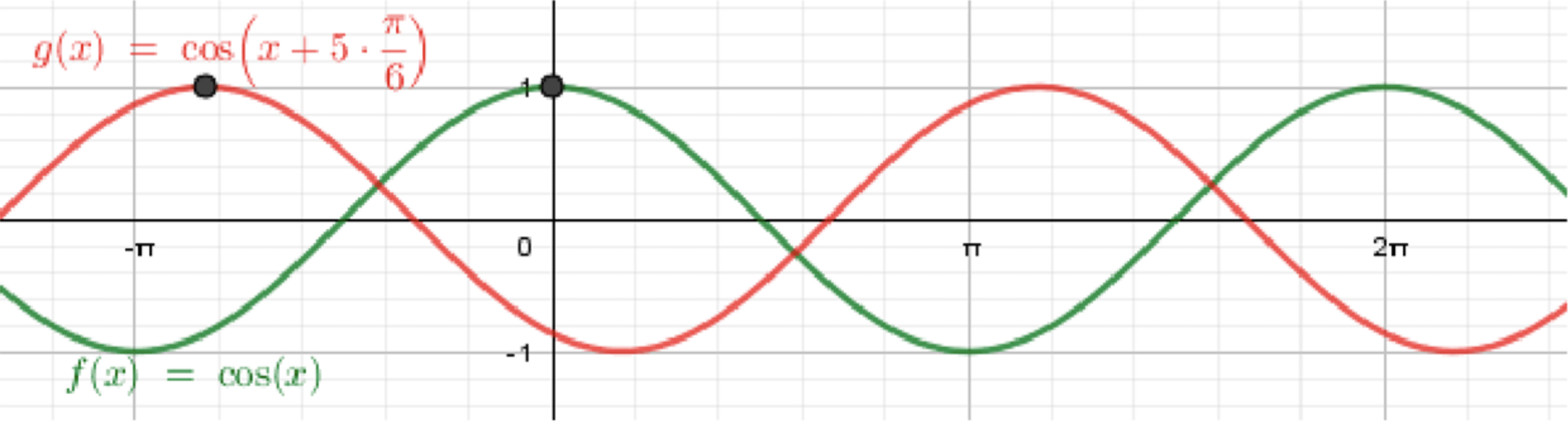
г) $y = \cos\left(x + \frac{5\pi}{6}\right);$

Построим график функции $y = \cos x;$

Переместим его на $\frac{5\pi}{6}$ единиц влево:

Общая памятка

Базовый косинус
$y=\cos x$: амплитуда $A=1$, период $T=2\pi$, средняя линия $y=0$.
Опорные точки за один период (например, $[0,2\pi]$):

$$(0,1),\quad \left(\tfrac{\pi}{2},0\right),\quad (\pi,-1),\quad \left(\tfrac{3\pi}{2},0\right),\quad (2\pi,1).$$

Горизонтальный сдвиг
$y=\cos(x-\varphi)$ — это график $y=\cos x$, сдвинутый вправо на $\varphi$.
$y=\cos(x+\varphi)=\cos(x-(-\varphi))$ — сдвиг влево на $\varphi$.
Период и амплитуда не меняются.
Ось «парной симметрии» графика $y=\cos(x-\varphi)$ — вертикальная прямая $x=\varphi$ (для $y=\cos(x+\varphi)$ — $x=-\varphi$).

Как строить руками (универсальный алгоритм)

• Наметить оси, сделать разметку по $x$ кратными $\tfrac{\pi}{6}$ или $\tfrac{\pi}{3}$ (как удобнее).
• Взять 5 «заводских» точек косинуса за один период и сдвинуть их на нужное $\pm\varphi$ по горизонтали.
• Соединить плавной волной: максимум → ноль → минимум → ноль → максимум.
• Повторить узор с шагом $2\pi$ в обе стороны по $x$.

а) $y=\cos\!\left(x+\tfrac{\pi}{2}\right)$

Смысл преобразования

• Это сдвиг влево на $\tfrac{\pi}{2}$.
• Эквивалентная форма: $\cos(x+\tfrac{\pi}{2})=-\sin x$. Полезно для понимания формы: это синусоида, отражённая по оси $x$.

Параметры

• Амплитуда $1$, период $2\pi$, средняя линия $y=0$.
• Ось симметрии: $x=-\tfrac{\pi}{2}$.
• Пересечение с осью $y$: $x=0\Rightarrow y=\cos\tfrac{\pi}{2}=0$.
• Нули: $x=\pi k$ (…,$-\pi,0,\pi,2\pi$, …).
• Максимумы: $x=-\tfrac{\pi}{2}+2\pi k$, значение $1$.
• Минимумы: $x=\tfrac{\pi}{2}+2\pi k$, значение $-1$.

Опорные точки (сдвигаем базовые на $-\tfrac{\pi}{2}$)

$$\left(-\tfrac{\pi}{2},1\right),\ (0,0),\ \left(\tfrac{\pi}{2},-1\right),\ (\pi,0),\ \left(\tfrac{3\pi}{2},1\right).$$

Как выглядит и как рисовать

• Волна проходит через начало координат, идя вниз (так как дальше в точке $\tfrac{\pi}{2}$ — минимум $-1$).
• Отметьте максимум в $x=-\tfrac{\pi}{2}$, ноль в $x=0$, минимум в $x=\tfrac{\pi}{2}$, ноль в $x=\pi$, снова максимум в $x=\tfrac{3\pi}{2}$.
• Повторите паттерн каждые $2\pi$ по $x$.

б) $y=\cos\!\left(x-\tfrac{2\pi}{3}\right)$

Смысл преобразования

• Сдвиг вправо на $\tfrac{2\pi}{3}$.

Параметры

• Амплитуда $1$, период $2\pi$, средняя линия $y=0$.
• Ось симметрии: $x=\tfrac{2\pi}{3}$.
• Пересечение с осью $y$: $y=\cos(-\tfrac{2\pi}{3})=\cos(\tfrac{2\pi}{3})=-\tfrac{1}{2}$.
• Нули: решаем $\cos(\,\cdot\,)=0\Rightarrow x-\tfrac{2\pi}{3}=\tfrac{\pi}{2}+\pi k\Rightarrow x=\tfrac{7\pi}{6}+\pi k$.
  В $[0,2\pi]$: $x=\tfrac{7\pi}{6},\ \tfrac{13\pi}{6}$.
• Максимумы: $x-\tfrac{2\pi}{3}=2\pi k\Rightarrow x=\tfrac{2\pi}{3}+2\pi k$, значение $1$.
• Минимумы: $x-\tfrac{2\pi}{3}=\pi+2\pi k\Rightarrow x=\tfrac{5\pi}{3}+2\pi k$, значение $-1$.

Опорные точки (сдвигаем базовые на $+\tfrac{2\pi}{3}$)

$$\left(\tfrac{2\pi}{3},1\right),\ \left(\tfrac{7\pi}{6},0\right),\ \left(\tfrac{5\pi}{3},-1\right),\ \left(\tfrac{13\pi}{6},0\right),\ \left(\tfrac{8\pi}{3},1\right).$$

Как выглядит и как рисовать

• Начинается «типичный» максимум не в $x=0$, а в $x=\tfrac{2\pi}{3}$.
• От него кривая убывает до нуля в $x=\tfrac{7\pi}{6}$, достигает минимума в $x=\tfrac{5\pi}{3}$, снова ноль в $x=\tfrac{13\pi}{6}$ и максимум в $x=\tfrac{8\pi}{3}$.
• Через $x=0$ график проходит на уровне $-\tfrac{1}{2}$.
• Повторяйте рисунок каждые $2\pi$ по $x$.

в) $y=\cos\!\left(x-\tfrac{\pi}{3}\right)$

Смысл преобразования

• Сдвиг вправо на $\tfrac{\pi}{3}$.

Параметры

• Амплитуда $1$, период $2\pi$, средняя линия $y=0$.
• Ось симметрии: $x=\tfrac{\pi}{3}$.
• Пересечение с осью $y$: $y=\cos(-\tfrac{\pi}{3})=\cos(\tfrac{\pi}{3})=\tfrac{1}{2}$.
• Нули: $x-\tfrac{\pi}{3}=\tfrac{\pi}{2}+\pi k\Rightarrow x=\tfrac{5\pi}{6}+\pi k$.
  В $[0,2\pi]$: $x=\tfrac{5\pi}{6},\ \tfrac{11\pi}{6}$.
• Максимумы: $x=\tfrac{\pi}{3}+2\pi k$, значение $1$.
• Минимумы: $x=\tfrac{4\pi}{3}+2\pi k$, значение $-1$.

Опорные точки (сдвигаем базовые на $+\tfrac{\pi}{3}$)

$$\left(\tfrac{\pi}{3},1\right),\ \left(\tfrac{5\pi}{6},0\right),\ \left(\tfrac{4\pi}{3},-1\right),\ \left(\tfrac{11\pi}{6},0\right),\ \left(\tfrac{7\pi}{3},1\right).$$

Как выглядит и как рисовать

• Максимум «переехал» в $x=\tfrac{\pi}{3}$.
• Дальше кривая опускается до нуля в $x=\tfrac{5\pi}{6}$, минимум в $x=\tfrac{4\pi}{3}$, ноль в $x=\tfrac{11\pi}{6}$, и снова максимум в $x=\tfrac{7\pi}{3}$.
• В точке $x=0$ значение $\tfrac{1}{2}$.
• Повторять узор с шагом $2\pi$.

г) $y=\cos\!\left(x+\tfrac{5\pi}{6}\right)$

Смысл преобразования

• Сдвиг влево на $\tfrac{5\pi}{6}$.

Параметры

• Амплитуда $1$, период $2\pi$, средняя линия $y=0$.
• Ось симметрии: $x=-\tfrac{5\pi}{6}$.
• Пересечение с осью $y$: $y=\cos\tfrac{5\pi}{6}=-\tfrac{\sqrt{3}}{2}$.
• Нули: $x+\tfrac{5\pi}{6}=\tfrac{\pi}{2}+\pi k\Rightarrow x=-\tfrac{\pi}{3}+\pi k$.
  В $[0,2\pi]$: $x=\tfrac{2\pi}{3},\ \tfrac{5\pi}{3}$.
• Максимумы: $x+\tfrac{5\pi}{6}=2\pi k\Rightarrow x=-\tfrac{5\pi}{6}+2\pi k$, значение $1$.
• Минимумы: $x+\tfrac{5\pi}{6}=\pi+2\pi k\Rightarrow x=\tfrac{\pi}{6}+2\pi k$, значение $-1$.

Опорные точки (сдвигаем базовые на $-\tfrac{5\pi}{6}$)

$$\left(-\tfrac{5\pi}{6},1\right),\ \left(-\tfrac{1\pi}{3},0\right)\!(=\!-\tfrac{\pi}{3}),\ \left(\tfrac{\pi}{6},-1\right),\ \left(\tfrac{2\pi}{3},0\right),\ \left(\tfrac{7\pi}{6},1\right).$$

(Пояснение к записи: вторая точка — $x=-\tfrac{\pi}{3}$, $y=0$.)

Как выглядит и как рисовать

• Максимум слева в $x=-\tfrac{5\pi}{6}$, затем ноль в $x=-\tfrac{\pi}{3}$, минимум в $x=\tfrac{\pi}{6}$, ноль в $x=\tfrac{2\pi}{3}$, максимум в $x=\tfrac{7\pi}{6}$.
• Через $x=0$ график проходит на уровне $-\tfrac{\sqrt{3}}{2}$.
• Повторяем узор через каждые $2\pi$.