ГДЗ 10-11 Класс Номер 11.6 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \cos x + 1$;

б) $y = \cos x — 2$;

в) $y = \cos x — \frac{1}{2}$;

г) $y = \cos x + 1,5$

Построить график функции:

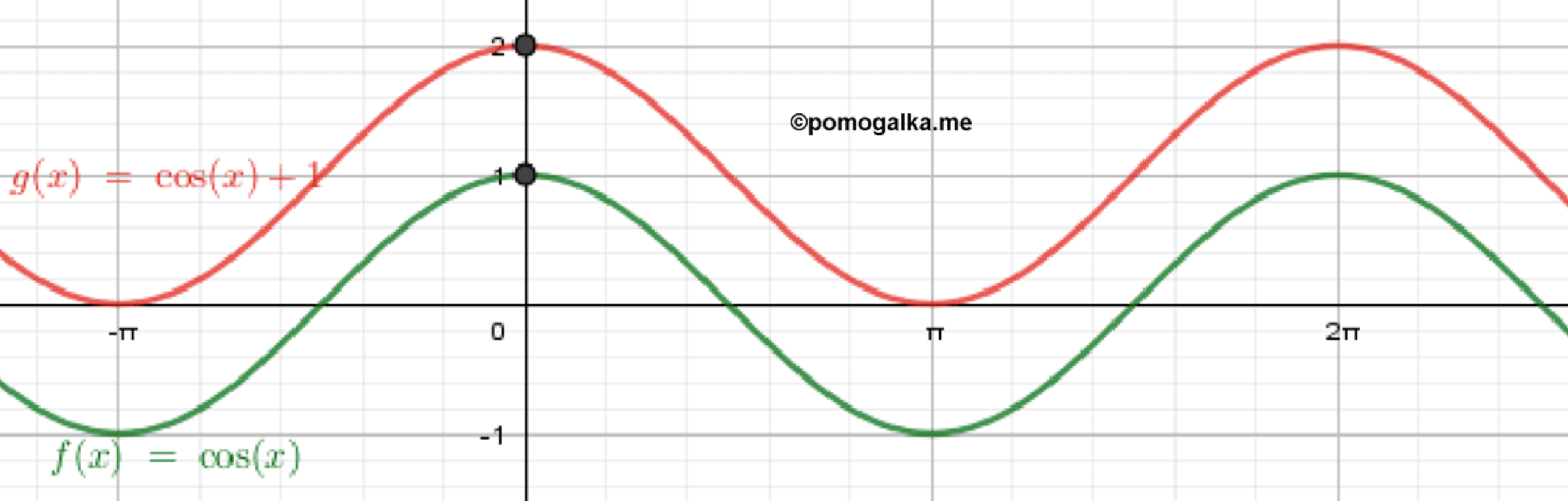
а) $y = \cos x + 1$;

Построим график функции $y = \cos x$;
Переместим его на 1 единицу вверх:

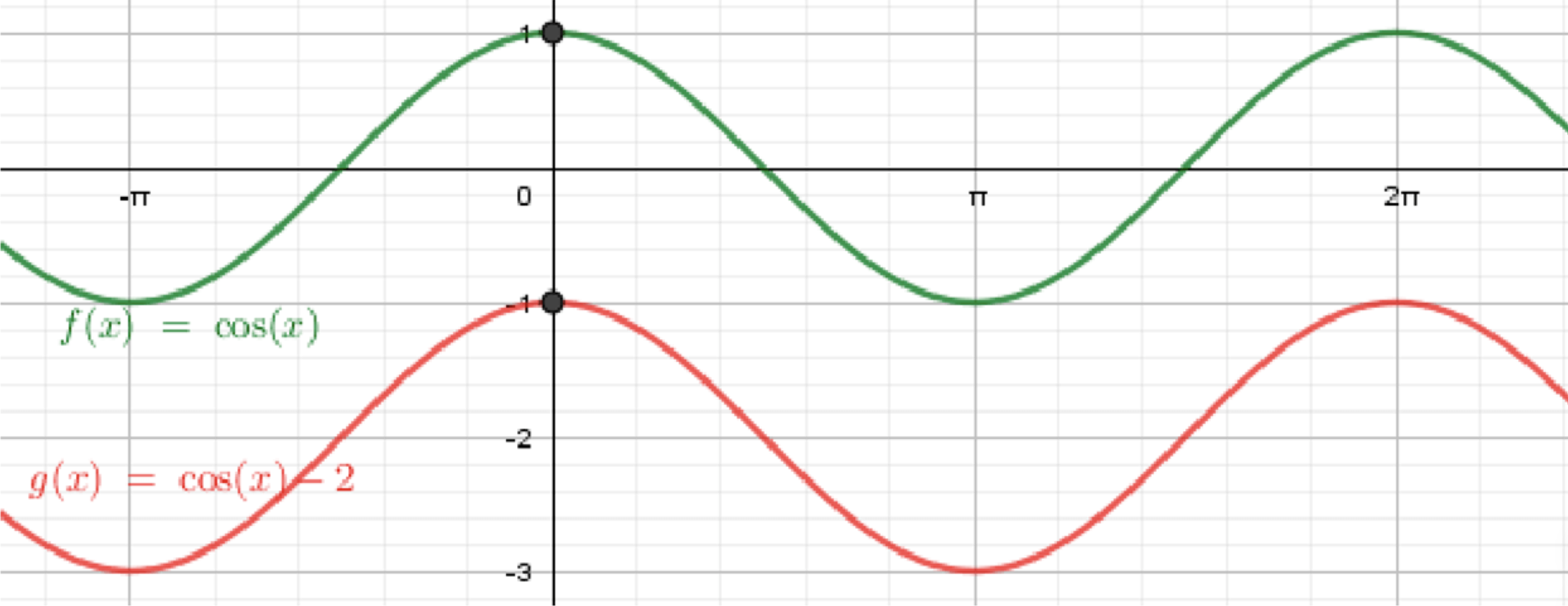
б) $y = \cos x — 2$;

Построим график функции $y = \cos x$;
Переместим его на 2 единицы вниз:

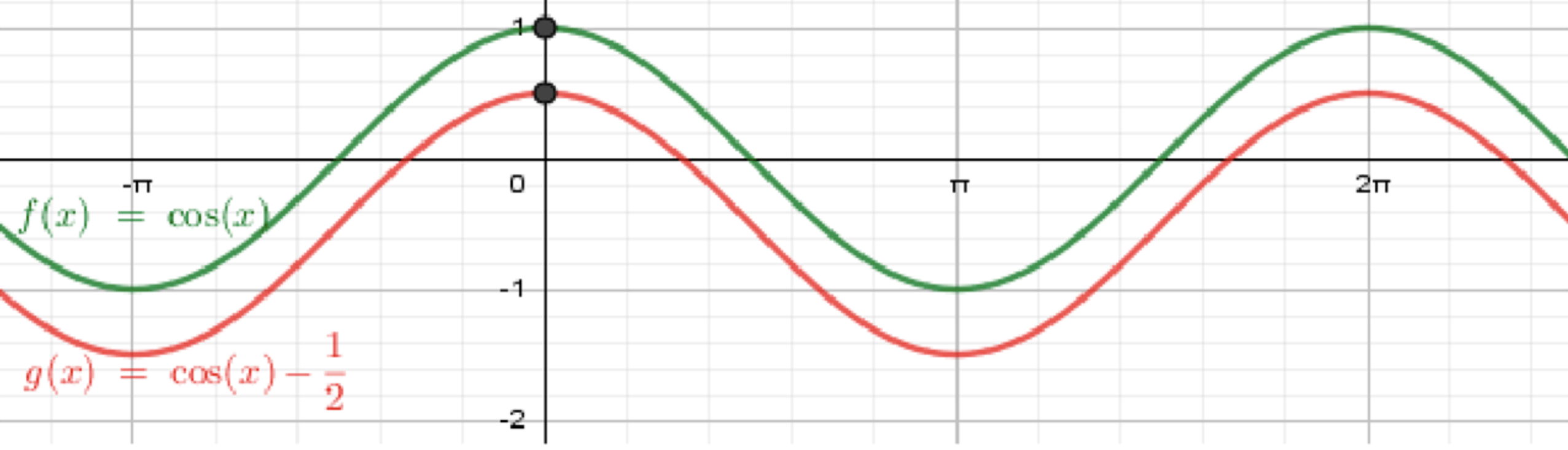
в) $y = \cos x — \frac{1}{2}$;

Построим график функции $y = \cos x$;
Переместим его на 0,5 единицы вниз:

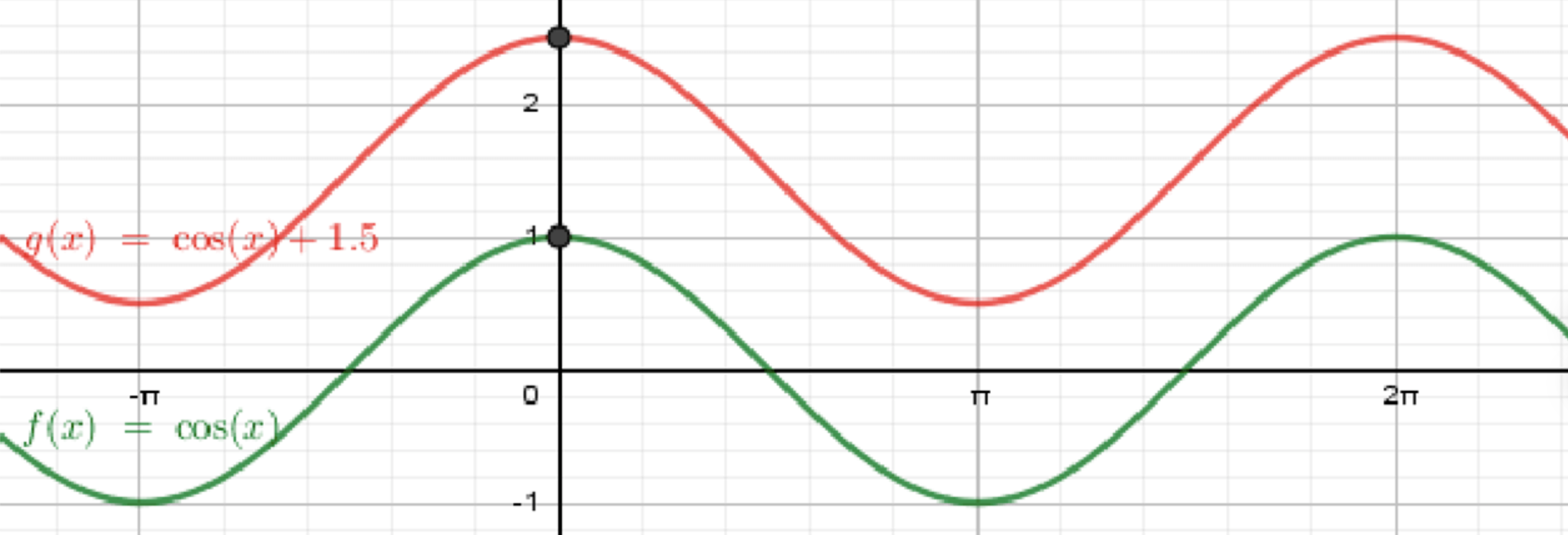
г) $y = \cos x + 1,5$;

Построим график функции $y = \cos x$;
Переместим его на 1,5 единицы вверх:

Общие факты 

• База: $y=\cos x$.
  Амплитуда $A=1$. Период $T=2\pi$. Средняя линия $y=0$.
  Опорные точки за один период $[0,2\pi]$:
  $(0,1)$, $\bigl(\tfrac{\pi}{2},0\bigr)$, $(\pi,-1)$, $\bigl(\tfrac{3\pi}{2},0\bigr)$, $(2\pi,1)$.
• Вертикальный сдвиг: $y=\cos x + d$.
  Амплитуда остаётся $1$, период остаётся $2\pi$, средняя линия становится $y=d$.
  Максимумы: $y_{\max}=d+1$ при $x=2\pi k$.
  Минимумы: $y_{\min}=d-1$ при $x=\pi+2\pi k$.
  Чётность: $\cos x$ — чётная ⇒ $\cos x+d$ тоже чётная ⇒ график симметричен относительно оси $Oy$.
  Точки перегиба: когда $\cos x=0$ ⇒ $x=\tfrac{\pi}{2}+\pi k$; по $y$ они лежат на средней линии $y=d$.
  Монотонность (на каждом периоде): убывает на $(0,\pi)+2\pi k$, возрастает на $(\pi,2\pi)+2\pi k$ — вертикальный сдвиг этого не меняет.

Алгоритм построения:

1. Провести горизонтальную среднюю линию $y=d$.
2. Выше и ниже неё отметить уровни $y=d+1$ (верхние пики) и $y=d-1$ (нижние впадины).
3. Расставить опорные $x$-координаты: $0$, $\tfrac{\pi}{2}$, $\pi$, $\tfrac{3\pi}{2}$, $2\pi$, затем повторять через $2\pi$.
4. На $x=0,2\pi,\dots$ ставим максимумы $y=d+1$; на $x=\pi,3\pi,\dots$ — минимумы $y=d-1$; на $x=\tfrac{\pi}{2},\tfrac{3\pi}{2},\dots$ — точки перегиба на уровне $y=d$.
5. Соединяем плавной косинусоидой (максимум → перегиб → минимум → перегиб → максимум) и «плиткуем» узор с шагом $2\pi$.

а) $y=\cos x+1$

Параметры.
$d=1$ ⇒ средняя линия $y=1$; амплитуда $1$; период $2\pi$.
Диапазон значений: $[0,2]$.
Максимумы: $y=2$ при $x=2\pi k$.
Минимумы: $y=0$ при $x=\pi+2\pi k$.
Пересечения с осями:

• $Oy$: $x=0\Rightarrow y=2$ (верхний пик).
• $Ox$: $\cos x+1=0\Rightarrow \cos x=-1\Rightarrow x=\pi+2\pi k$ (совпадают с минимумами).

Опорные точки на $[0,2\pi]$:

$$\begin{aligned} x=0&:\ y=2;\\ x=\tfrac{\pi}{2}&:\ y=1;\\ x=\pi&:\ y=0;\\ x=\tfrac{3\pi}{2}&:\ y=1;\\ x=2\pi&:\ y=2;\\ \text{доп.: }x=\tfrac{\pi}{3}&:\ y=\tfrac{3}{2};\quad x=\tfrac{2\pi}{3}:\ y=\tfrac{1}{2}. \end{aligned}$$

Как выглядит.
Вся волна косинуса поднята на 1: «вершины» на $y=2$, «впадины» касаются $Ox$ на $y=0$. График чётный, симметрия относительно $Oy$ сохранена.

Как строить.
Проведите $y=1$, отметьте уровни $y=2$ и $y=0$, поставьте точки в $x=0,\tfrac{\pi}{2},\pi,\tfrac{3\pi}{2},2\pi$ с указанными $y$, соедините плавно и повторите рисунок каждые $2\pi$.

б) $y=\cos x-2$

Параметры.
$d=-2$ ⇒ средняя линия $y=-2$; амплитуда $1$; период $2\pi$.
Диапазон значений: $[-3,-1]$.
Максимумы: $y=-1$ при $x=2\pi k$.
Минимумы: $y=-3$ при $x=\pi+2\pi k$.
Пересечения с осями:

• $Oy$: $x=0\Rightarrow y=-1$.
• $Ox$: $\cos x-2=0\Rightarrow \cos x=2$ — нет решений, т.е. график не пересекает $Ox$ (лежит целиком ниже оси $Ox$).

Опорные точки на $[0,2\pi]$:

$$x=0:-1;x=\frac{\pi }{2}:-2;x=\pi :-3;$$

$$x=0:\ -1;\quad x=\tfrac{\pi}{2}:\ -2;\quad x=\pi:\ -3;\quad x=\tfrac{3\pi}{2}:\ -2;\quad x=2\pi:\ -1.$$

Как выглядит.
Косинус опущен на 2: колеблется между $-3$ и $-1$, «середина» на $y=-2$. Никаких нулей.

Как строить.
Проведите $y=-2$, отметьте $y=-1$ и $y=-3$, расставьте опорные точки, соедините плавной волной, повторяйте через $2\pi$.

в) $y=\cos x-\tfrac{1}{2}$

Параметры.
$d=-\tfrac{1}{2}$ ⇒ средняя линия $y=-\tfrac{1}{2}$; амплитуда $1$; период $2\pi$.
Максимумы: $y=\tfrac{1}{2}$ при $x=2\pi k$.
Минимумы: $y=-\tfrac{3}{2}$ при $x=\pi+2\pi k$.
Пересечения с осями:

• $Oy$: $x=0\Rightarrow y=\tfrac{1}{2}$ (верхняя граница диапазона).
• $Ox$: $\cos x-\tfrac{1}{2}=0\Rightarrow \cos x=\tfrac{1}{2}\Rightarrow x=2\pi k\pm \tfrac{\pi}{3}$.
  На $[0,2\pi]$: $x=\tfrac{\pi}{3}$ и $x=\tfrac{5\pi}{3}$.

Опорные точки на $[0,2\pi]$:

$$\begin{aligned} x=0&:\ \tfrac{1}{2};\quad x=\tfrac{\pi}{3}:\ 0;\quad x=\tfrac{\pi}{2}:\ -\tfrac{1}{2};\quad x=\tfrac{2\pi}{3}:\ -1;\\ x=\pi&:\ -\tfrac{3}{2};\quad x=\tfrac{3\pi}{2}:\ -\tfrac{1}{2};\quad x=\tfrac{5\pi}{3}:\ 0;\quad x=2\pi:\ \tfrac{1}{2}. \end{aligned}$$

Как выглядит.
Волна опущена на $0{,}5$: верх — $y=\tfrac{1}{2}$, низ — $y=-\tfrac{3}{2}$. Есть два нуля в каждом периоде: при $x=\pm \tfrac{\pi}{3}$ (с точностью до добавления $2\pi k$). Симметрия относительно $Oy$ сохраняется.

Как строить.
Проведите $y=-\tfrac{1}{2}$, отметьте уровни $\tfrac{1}{2}$ и $-\tfrac{3}{2}$, поставьте нули в $x=\tfrac{\pi}{3}$ и $\tfrac{5\pi}{3}$, добавьте вершины/впадины и перегибы, соедините плавно, повторяйте через $2\pi$.

г) $y=\cos x+1{,}5$

Параметры.
$d=1{,}5$ ⇒ средняя линия $y=1{,}5$; амплитуда $1$; период $2\pi$.
Диапазон значений: $[0{,}5,\ 2{,}5]$.
Максимумы: $y=2{,}5$ при $x=2\pi k$.
Минимумы: $y=0{,}5$ при $x=\pi+2\pi k$.
Пересечения с осями:

• $Oy$: $x=0\Rightarrow y=2{,}5$.
• $Ox$: $\cos x+1{,}5=0\Rightarrow \cos x=-1{,}5$ — нет решений, т.е. график не пересекает $Ox$ (вся кривая выше оси $Ox$).

Опорные точки на $[0,2\pi]$:

$$x=0:\mathrm{2,5};x=\frac{\pi }{2}:\mathrm{1,5};x=\pi :\mathrm{0,5};x=\frac{3\pi }{2}:\mathrm{1,5};$$

$$x=0:\ 2{,}5;\quad x=\tfrac{\pi}{2}:\ 1{,}5;\quad x=\pi:\ 0{,}5;\quad x=\tfrac{3\pi}{2}:\ 1{,}5;\quad x=2\pi:\ 2{,}5;\quad \text{доп.: }x=\tfrac{\pi}{3}:\ 2;\ x=\tfrac{2\pi}{3}:\ 1.$$

Как выглядит.
Вся косинусоида приподнята на $1{,}5$: колеблется над осью $Ox$ между $0{,}5$ и $2{,}5$. Нулей нет.

Как строить.
Проведите $y=1{,}5$, отметьте $y=2{,}5$ и $y=0{,}5$, расставьте опорные точки, соедините плавно, повторяйте рисунок через $2\pi$.