Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 11.9 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте и прочитайте график функции у = f(x):
а)
б)
в)
г)
Построить и прочитать график функции :
В данной задаче — целое неотрицательное число;
а)
- — уравнение синусоиды:
- — уравнение прямой:
График функции:
Свойства функции:
- Возрастает на
- Убывает на
- на
- на
- Ограничена сверху;
- Ни четная, ни нечетная;
- Не является периодической;
- Непрерывна на
б)
- — уравнение синусоиды:
- — уравнение синусоиды:
График функции:
Свойства функции:
- Возрастает на
- Убывает на
- на
- на
- Ограничена снизу и сверху;
- Ни четная, ни нечетная;
- Не является периодической;
- Непрерывна на
в)
- — уравнение синусоиды:
- — уравнение гиперболы:
График функции:
Свойства функции:
- Возрастает на
- Убывает на
- на
- на
- Ограничена снизу;
- Ни четная, ни нечетная;
- Не является периодической;
- Непрерывна на
г)
- — уравнение синусоиды:
- — уравнение параболы:
График функции:
Свойства функции:
- Возрастает на
- Убывает на
- на
- на
- Ограничена снизу;
- Ни четная, ни нечетная;
- Не является периодической;
- Непрерывна на
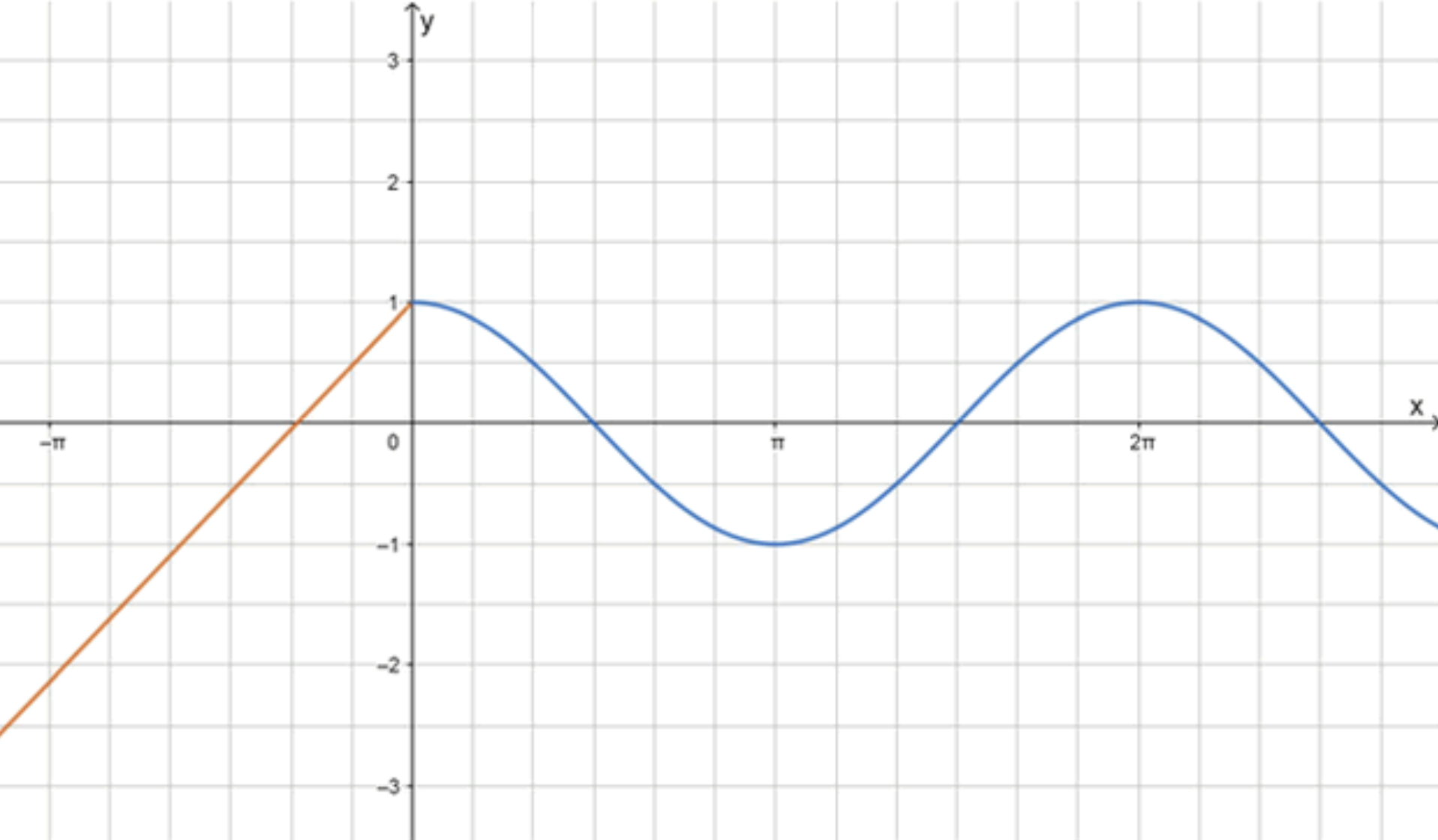
а)
1) Область определения
Обе ветви определены на своих кусках, точка берётся из правой ветви ( существует).
Следовательно, .
2) Непрерывность и склейка в
.
Значит, разрывов нет, непрерывна на .
Дифференцируемость в 0.
,
.
Левые и правые производные различаются ⇒ в недифференцируема (угловая точка).
3) Монотонность
- На : монотонно возрастает (угол наклона ).
- На : рассматриваем .
- убывает на отрезках ,
- возрастает на , где .
С учётом , берём только те отрезки, которые лежат в .
Итого:
- возрастает на ;
- убывает на .
4) Экстремумы
На правой ветви локальные максимумы в точках (), значение ; локальные минимумы при (), значение .
Глобального минимума нет (левая ветвь уходит к ).
Глобальный максимум достигается (например, при ).
5) Значения (множество значений)
Слева при , а сверху обе ветви не превышают 1 (и значение 1 достигается).
Значит, .
(В исходном конспекте было «», но это противоречит ; правильно — с квадратной скобкой.)
6) Знаки
- Для : . На левой ветви это интервал (плюс можно добавить отдельно с правой ветви: ).
- Для : .
Итого:
- на .
(Обычно точку в записях опускают, т.к. это «одна точка», но формально .) - на .
7) Нули (пересечения с )
.
, , причём берём : .
8) Чётность, периодичность
Не чётная и не нечётная (левая и правая ветви разные), не периодическая.
График:
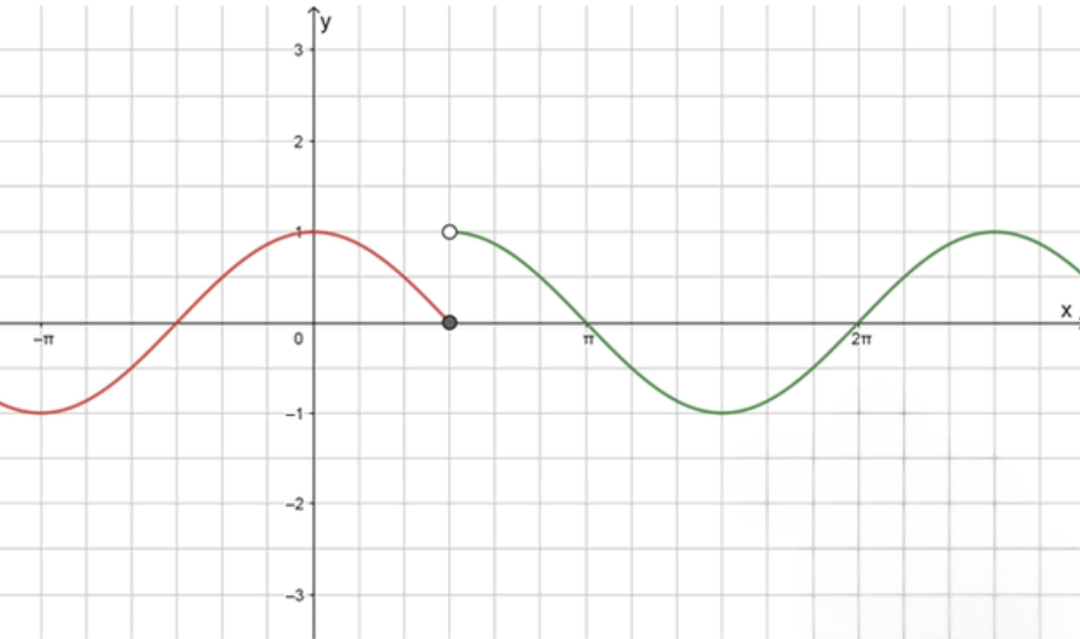
б)
1) Область определения
Обе функции определены везде, значит .
2) Непрерывность и склейка в
Левый предел: .
Правый предел (и значения справа близко к точке): .
Точка относится к левой ветви ⇒ .
Имеем скачок: левое значение 0, правое «стартует» с 1 ⇒ функция разрывна в .
3) Монотонность
- На работает : убывает на , возрастает на для всех , ограничивая правым концом .
- На работает : возрастает на , убывает на , .
(Если переписать кратко по «стандартным» кускам: «лево — как у , право — как у », с учётом соответствующих пересечений с и .)
4) Экстремумы
- На левом куске у локальные максимумы при (значение ), локальные минимумы при (значение ); учитываем только те, что .
- На правом куске у локальные максимумы при (значение ), но точка не входит в правый кусок, поэтому первый максимум при ; минимумы при (значение ).
Глобальные: (достигается, напр. слева и справа), (много точек).
5) Значения
И слева, и справа значения лежат в . И оба края достигаются ⇒ .
6) Знаки
- Слева (): на ; на смежных интервалах.
- Справа (): на , на .
Точка : .
7) Нули
- Слева: , берём все : .
- Справа: , но нужно : .
8) Чётность/периодичность
Не чётная, не нечётная, не периодическая (из-за «ломки» в ).
График:
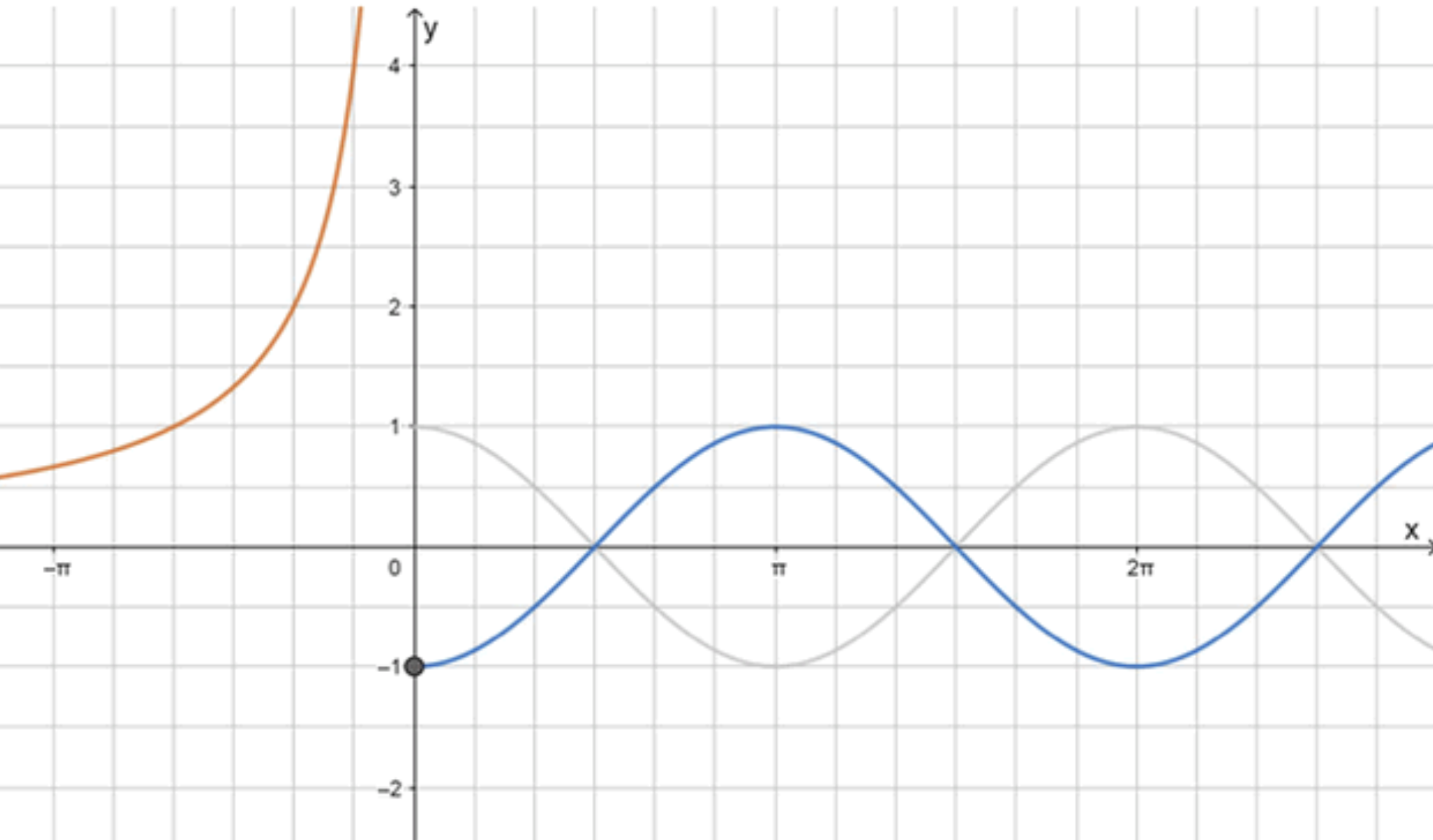
в)
1) Область определения
Обе ветви определены на своих кусках (левая — на , правая — на ).
.
2) Непрерывность и поведение у
(вертикальная асимптота слева).
.
Правый предел конечен, левый бесконечен ⇒ разрыв первого рода отсутствует, разрыв бесконечного типа в . Непрерывна на и на .
3) Монотонность
- На : , ⇒ строго возрастает на всём .
- На : возрастает на и убывает на , .
4) Экстремумы
- На правой ветви локальные максимумы в : ; локальные минимумы в : (учитывая ).
- Глобальный минимум: достигается (например, ).
- Глобального максимума нет (левая ветвь при ).
5) Значения и асимптоты
- Слева и не ограничена сверху; при , ⇒ горизонтальная асимптота слева.
- Справа .
Итого .
6) Знаки
- На : .
- На : ;
.
7) Нули
Левая ветвь корней не имеет.
Правая: , берём : .
8) Чётность/периодичность
Не чётная, не нечётная, не периодическая.
График:
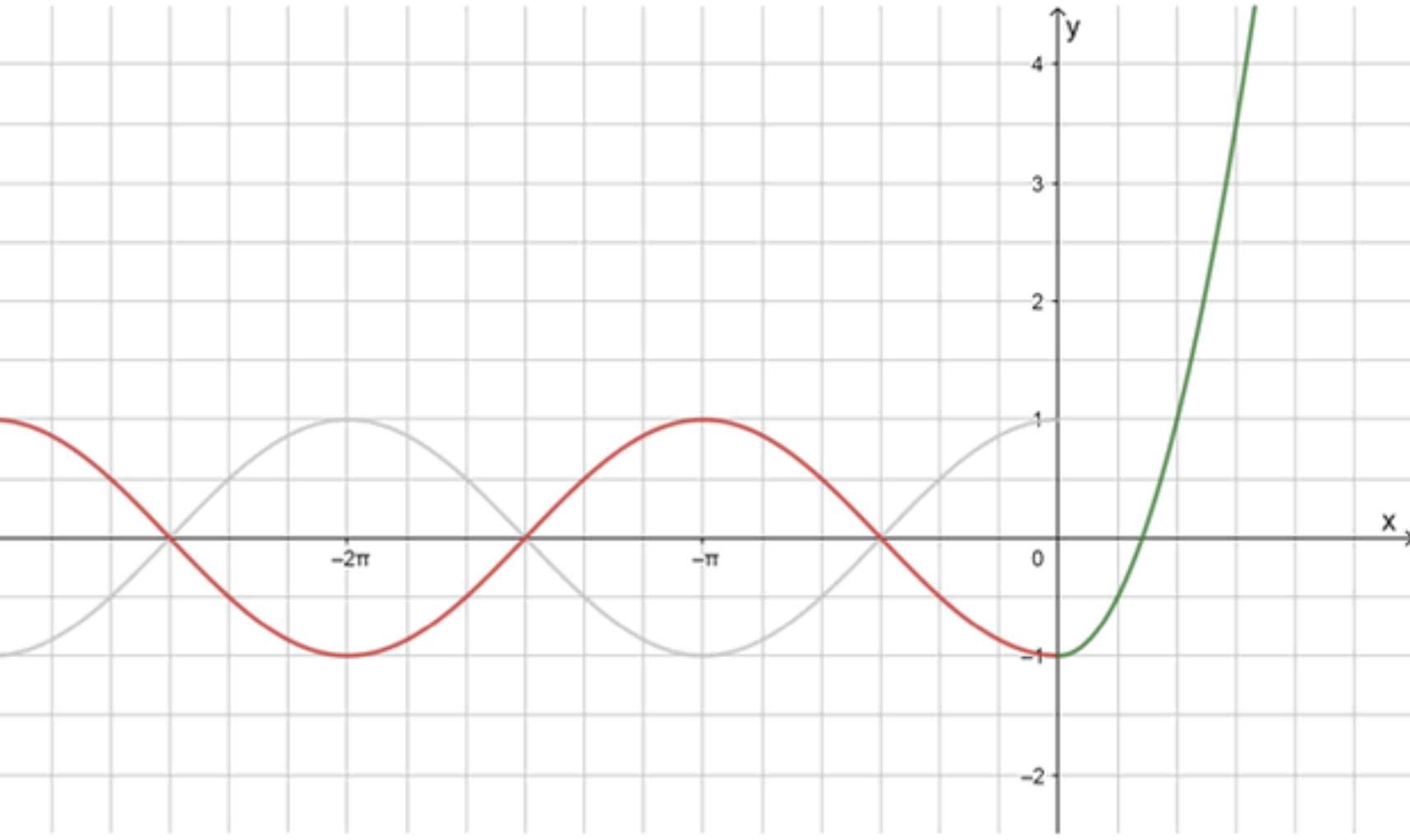
г)
1) Область определения
Обе ветви определены на своих кусках ⇒ .
2) Непрерывность и гладкость в
слева, справа ⇒ непрерывна в 0 и на всей .
Производные в 0.
Слева .
Справа .
Итак, дифференцируема в 0 (даже ).
Вторые производные: слева ; справа — вторые производные не совпадают (не ).
3) Монотонность
- На : ведёт себя по стандартным интервалам, но на отрицательной полуоси.
Напомним: убывает на и возрастает на . Для наоборот. Сдвигая на отрицательную полуось:- возрастает на ,
- убывает на ,
где , и всё это .
- На : возрастает на (производная , равна нулю только в 0).
Итого кратко: возрастает на ; убывает на .
4) Экстремумы
- На левом куске у локальные минимумы в (значение ), локальные максимумы в (значение ).
- В правый кусок имеет минимум (вершина параболы): .
Глобальный минимум достигается многократно (включая ). Глобального максимума нет (правая ветвь ).
5) Значения
Правая ветвь , левая .
Совокупно .
6) Знаки
- Слева: (движемся к );
на соседних промежутках. - Справа: , при , на .
7) Нули
- Слева: для : .
- Справа: , но .
8) Чётность/периодичность
Не чётная, не нечётная, не периодическая.
График: