ГДЗ 10-11 Класс Номер 12.1 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

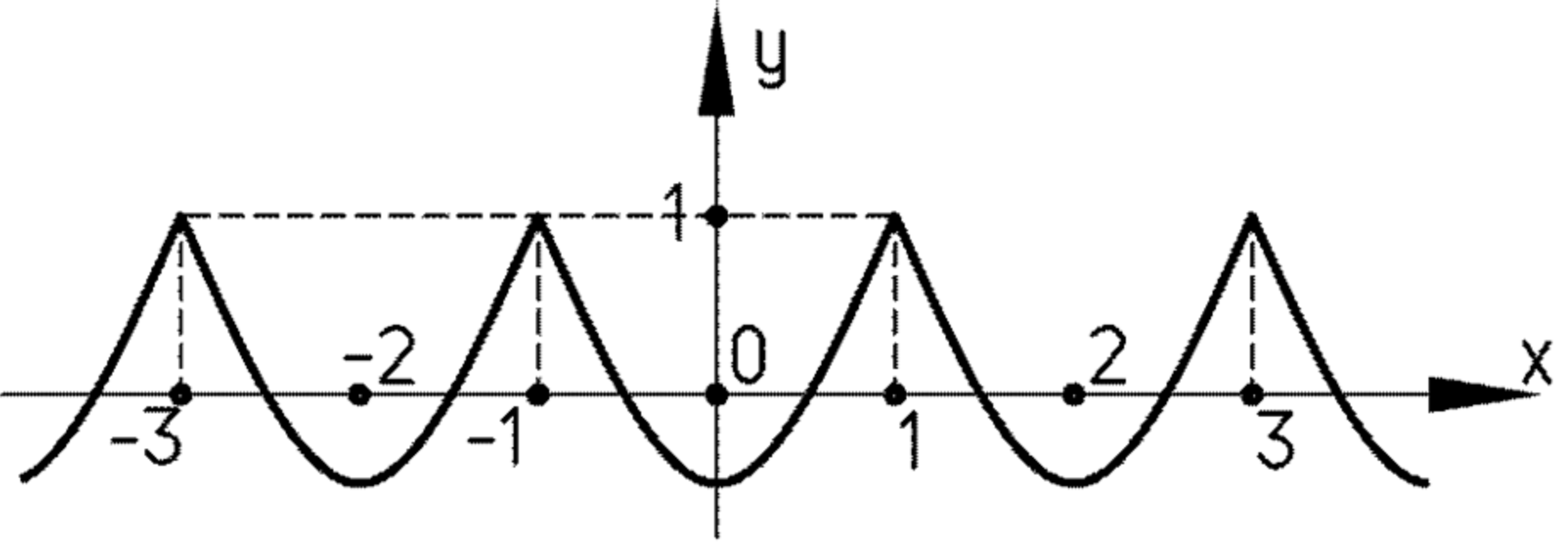
На рисунке 11 изображена часть графика периодической функции у = f(x) на отрезке [-1; 1], длина которого равна периоду функции. Постройте график функции:

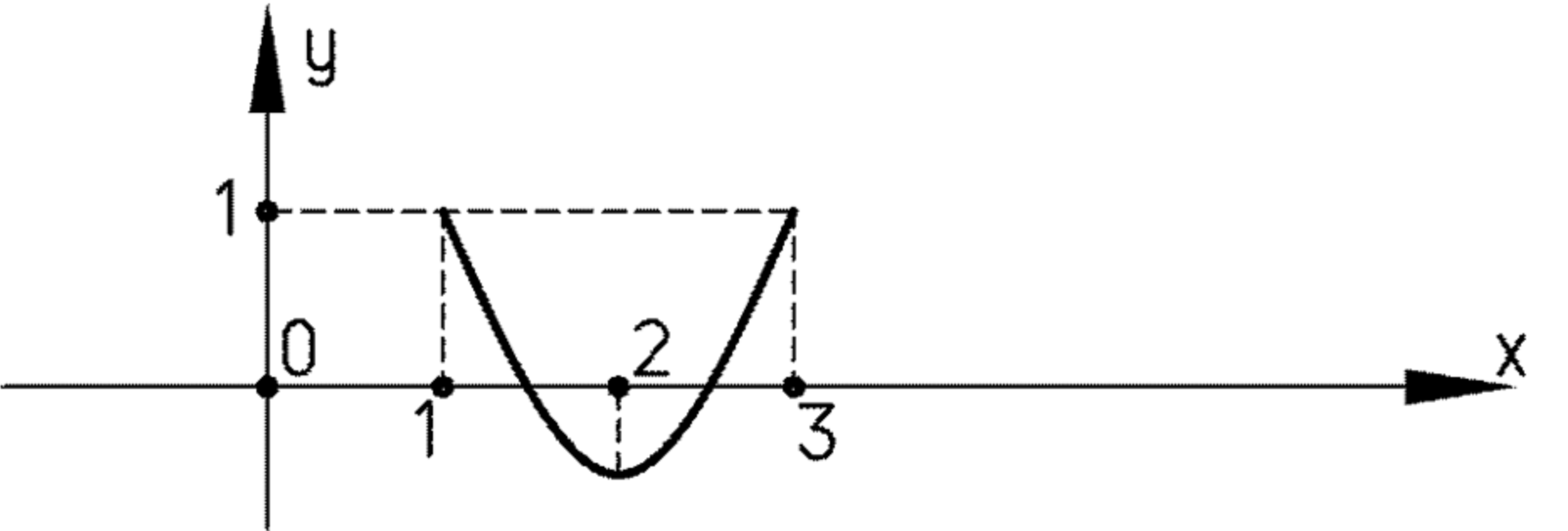
а) на отрезке [1; 3];

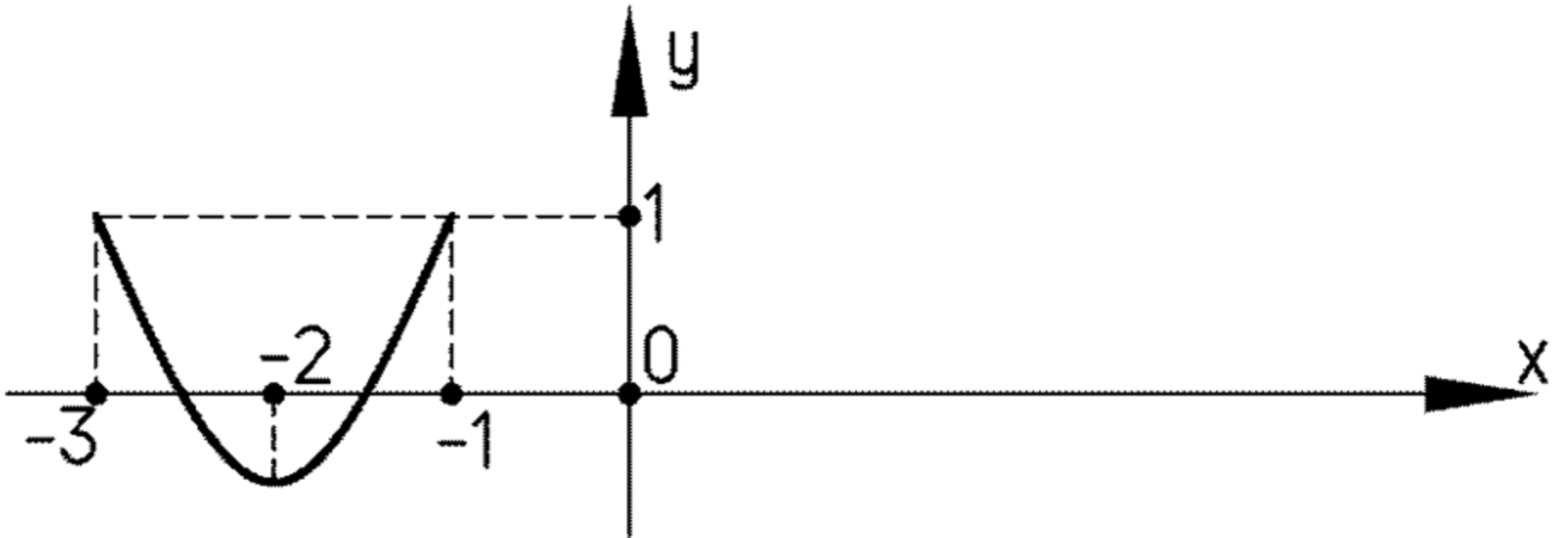
б) на отрезке [-3; -1];

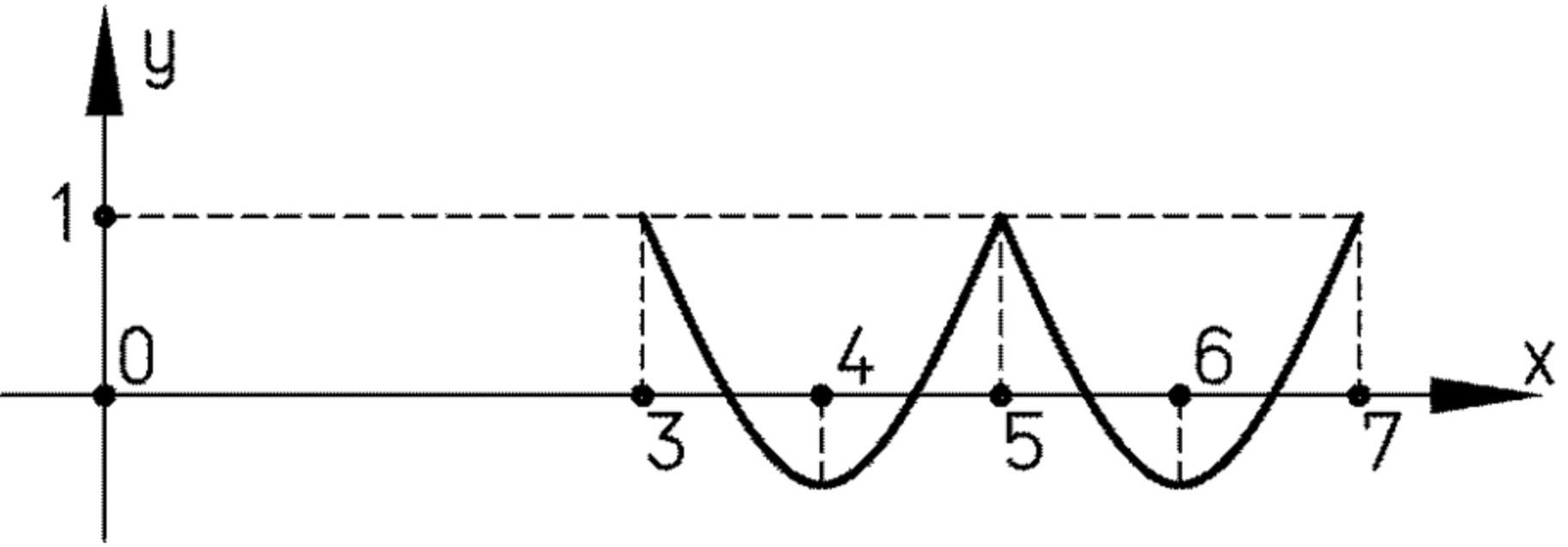
в) на отрезке [3; 7];

г) на всей числовой прямой.

На рисунке 11 изображена часть графика периодической функции $y=f(x)$ на отрезке $[-1;1]$, длина которого равна периоду функции:

а) На отрезке $[1;3]$:

б) На отрезке $[-3;-1]$:

в) На отрезке $[3;7]$:

г) На всей числовой прямой:

Сразу зафиксируем ключевой факт: на рисунке дана часть графика на отрезке $[-1;1]$, и длина этого отрезка равна периоду функции. Значит:

• Период $T=2$.
• Для любых $x$ и целых $k$:$$f(x+2k)=f(x)\mathrm{.}$$
• Базовый («опорный») фрагмент графика — это весь график на $[-1;1]$. Остальное получается простыми горизонтальными сдвигами этого фрагмента на целое число периодов.

Чтобы не задваивать точки на границах периодов (в местах $x=\dots ,-3,-1,1,3,\dots$), удобно придерживаться правила: в каждом копируемом отрезке включаем левую границу и исключаем правую. Например, $[-1,1)$, $[1,3)$, $[3,5)$ и т. д. (Это чисто техническая тонкость, если рисуешь от руки — просто следи, чтобы «стыки» не получались толще.)

Обозначим базовый фрагмент:

$$S=\{(x,f(x)):x\in [-1,1]\}\mathrm{.}$$

Тогда всякий сдвиг на $2k$ даёт фрагмент

$$S_k=\{(x+2k,f(x)):x\in [-1,1]\}\mathrm{.}$$

Иными словами, график на каждом отрезке $[2k-1,2k+1]$ — это точная копия базового куска, сдвинутая по горизонтали на $2k$.

Эквивалентно, чтобы найти значение $f$ в любой точке $x$, «верни» аргумент в базовый интервал $[-1,1]$ на ближайшее целое число периодов. Удобная формула:

$$k(x)=\lfloor \frac{x+1}{2}\rfloor ,x_{\text{red}}=x-2k(x)\in [-1,1),f(x)=f\left(x_{\text{red}}\right)\mathrm{.}$$

(Здесь $\lfloor \cdot \rfloor$ — пол, «целая часть вниз».)

а) Построение на отрезке $[1;3]$

Это ровно один период вправо от $[-1;1]$:
$[1;3]=[-1;1]+2$.

Как рисовать:

1. Возьми весь видимый на рисунке фрагмент на $[-1;1]$.
2. Сдвинь его вправо на 2 (каждую точку $(x,y)$ замени на $(x+2,y)$).
3. Отрисуй получившуюся копию на $[1;3]$.

Формула соответствия точек:

$$\text{Для }x\in [1,3]\text{\hspace{0.17em}⁣}:f(x)=f(x-2),x-2\in [-1,1]\mathrm{.}$$

Мини-чек: если на базовом куске есть особая точка при $x=x_0$ (например, ноль функции, максимум, излом), то на $[1;3]$ эта же особенность будет при $x=x_0+2$.

б) Построение на отрезке $[-3;-1]$

Это ровно один период влево от $[-1;1]$:
$[-3;-1]=[-1;1]-2$.

Как рисовать:

1. Возьми фрагмент $[-1;1]$.
2. Сдвинь его влево на 2 (каждую точку $(x,y)$ замени на $(x-2,y)$).
3. Получится точная копия на $[-3;-1]$.

Формула соответствия:

$$\text{Для }x\in [-3,-1]\text{\hspace{0.17em}⁣}:f(x)=f(x+2),x+2\in [-1,1]\mathrm{.}$$

Опять же, любая характерная точка $x_0\in [-1,1]$ переедет в $x_0-2$.

в) Построение на отрезке $[3;7]$

Длина $[3;7]$ равна $4$, это два полных периода. Удобно разбить на два периодических блока длиной $2$:

• $[3;5]=[-1;1]+4$ — сдвиг на $+4$ (то есть $k=2$),
• $[5;7]=[-1;1]+6$ — сдвиг на $+6$ (то есть $k=3$).

Как рисовать пошагово:

1. Скопируй базовый фрагмент $[-1;1]$ и сдвинь его вправо на 4 → получишь участок на $[3;5]$.
2. Ещё раз скопируй базовый фрагмент и сдвинь его вправо на 6 → получишь участок на $[5;7]$.
3. Соедини их подряд — получится график на всём $[3;7]$.

Формулы соответствия:

$$\begin{array}{rl}{\displaystyle }& {\displaystyle x\in [3,5]\text{\hspace{0.17em}⁣}:f(x)=f(x-4),x-4\in [-1,1],}\\ {\displaystyle }& {\displaystyle x\in [5,7]\text{\hspace{0.17em}⁣}:f(x)=f(x-6),x-6\in [-1,1]\mathrm{.}}\end{array}$$

г) Построение на всей числовой прямой

Повторяем базовый кусок $[-1;1]$ для всех целых сдвигов на $2k$:

$$\text{График }y=f(x)\text{ на }\mathbb{R}=\bigcup _{k\in \mathbb{Z}}\{(x+2k,f(x)):x\in [-1,1]\}\mathrm{.}$$

Эквивалентная практическая формула (алгоритм «верни в базовый интервал»):

1. Для произвольного $x$ вычисли $k=\lfloor \frac{x+1}{2}\rfloor$.
2. Положи $x_{\text{red}}=x-2k\in [-1,1)$.
3. Возьми значение (и «форму» графика) в точке $x_{\text{red}}$ на базовом рисунке — это и есть $f(x)$.

Полезные подсказки для аккуратного чертежа

• Стыки периодов. Все особенности, находящиеся в окрестности $x=-1$ и $x=1$ на базовом куске, будут повторяться во всех точках $x=2k\pm 1$. Если в исходном рисунке в $x=1$ есть разрыв, излом или максимум — ровно тот же тип особенности будет в каждой такой точке.
• Нули, экстремумы, вершины. Если на $[-1,1]$ нуль при $x=x_0$, то нули будут в $x=x_0+2k$. Если максимум при $x=m$, то максимумы в $x=m+2k$. И так далее.
• Масштаб по оси $y$ не меняется — только горизонтальные сдвиги.
• Чтобы ничего не потерять, можно проставить на базовом куске несколько ориентиров (например, отмеченные точки $A(x_A,y_A),B(x_B,y_B)$ и т. п.) и затем разметить их копии $A_k(x_A+2k,y_A)$, $B_k(x_B+2k,y_B)$.