ГДЗ 10-11 Класс Номер 12.2 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

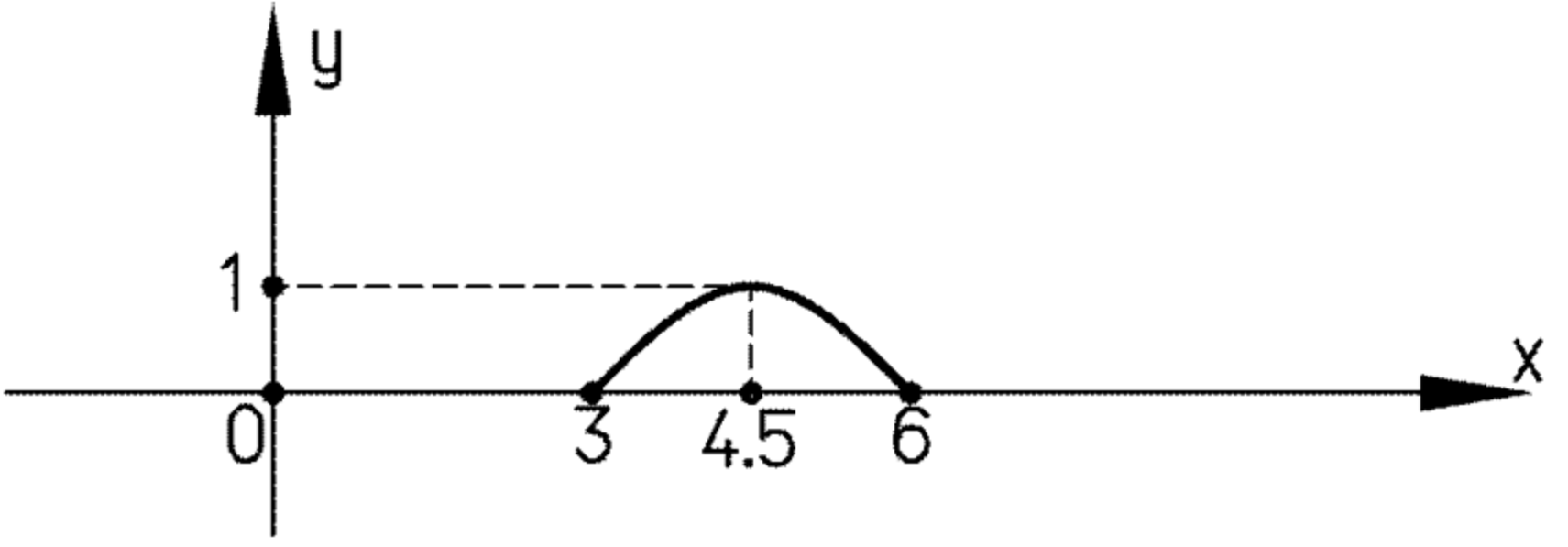
На рисунке 12 изображена часть графика периодической функции у = f(x) на отрезке [0; 3], длина которого равна периоду функции. Постройте график функции:

а) на отрезке [3; 6];

б) на отрезке [-3; 0];

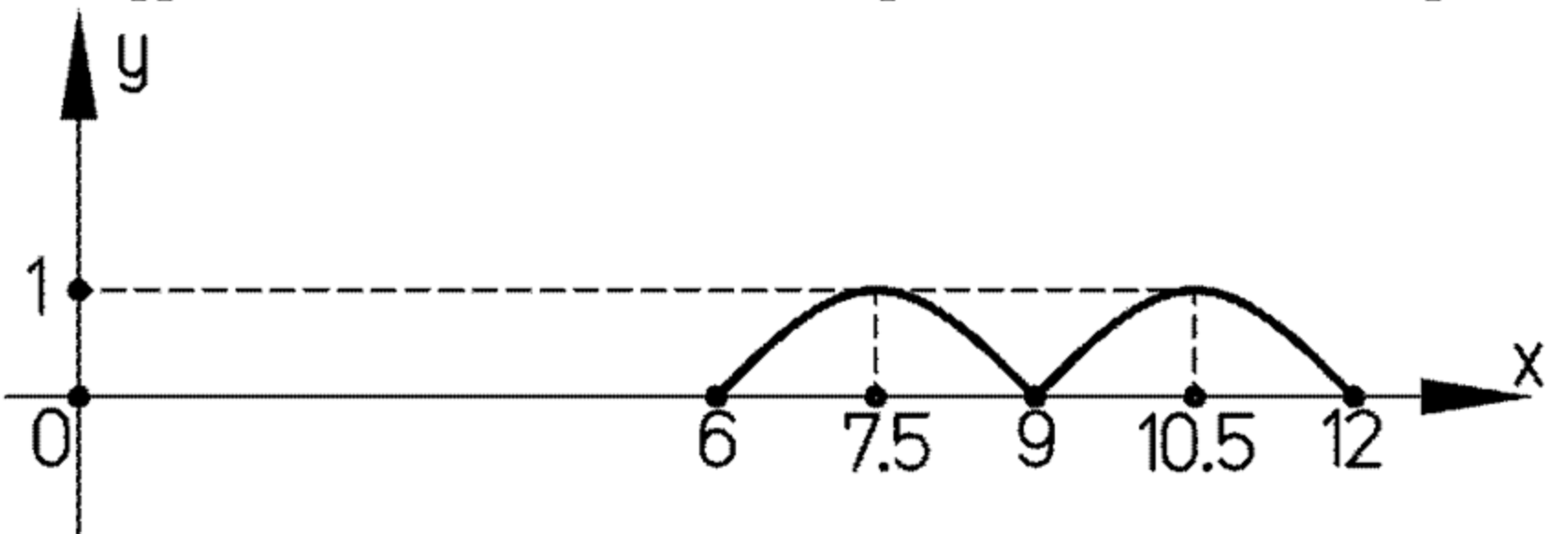
в) на отрезке [6; 12];

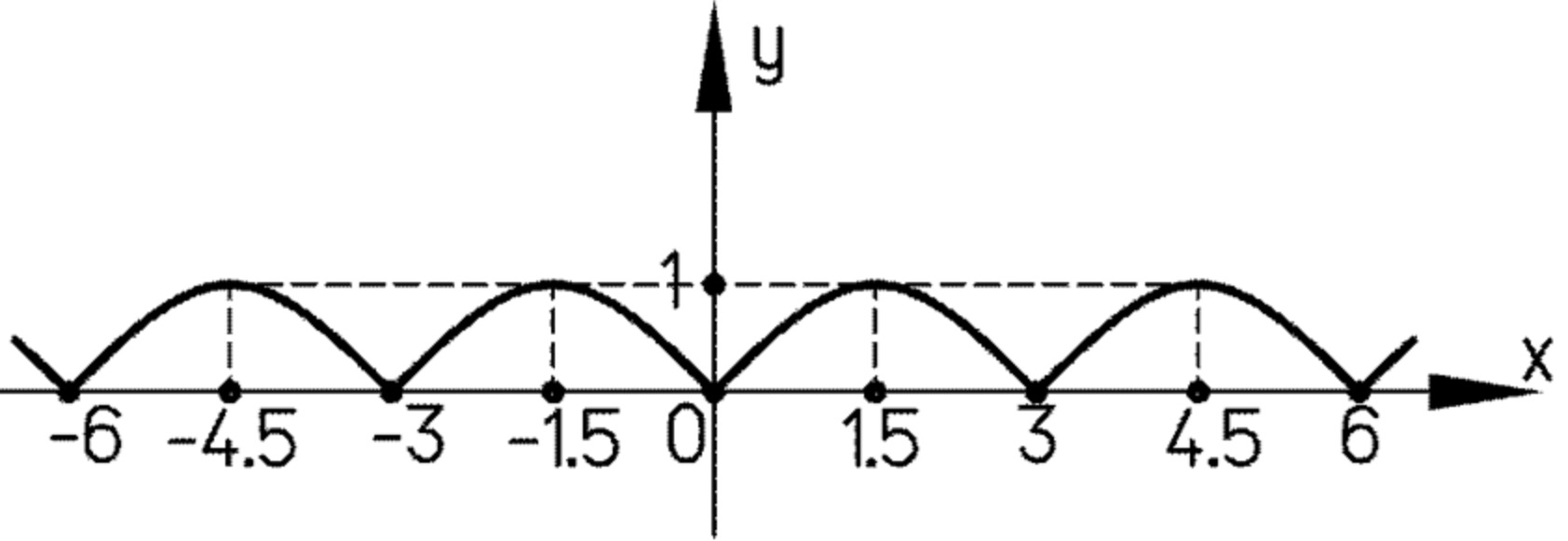
г) на всей числовой прямой.

На рисунке 12 изображена часть графика периодической функции $y = f(x)$ на отрезке $[0; 3]$, длина которого равна периоду функции:

а) На отрезке $[3; 6]$:

б) На отрезке $[-3; 0]$:

в) На отрезке $[6; 12]$:

г) На всей числовой прямой:

На рисунке 12 показан «опорный» фрагмент графика $y=f(x)$ на отрезке $[0;3]$. Сказано, что длина этого отрезка равна периоду, значит

$$T=3,\qquad f(x+3)=f(x)\ \ \text{для всех }x.$$

Иначе говоря, весь график получается простым горизонтальным повторением участка $[0;3]$ через каждые 3 единицы по оси $x$.

Чтобы не «дублировать» точки на стыках периодов (в $x=3k$), удобно мысленно считать базовый фрагмент как $[0,3)$, а копии — $[3,6)$, $[6,9)$ и т. д. (левая граница включена, правая — нет). От этого сам график не меняется, это лишь аккуратность в отрисовке.

Полезный универсальный приём «сведения к базовому интервалу»:

$$k(x)=\left\lfloor \frac{x}{3}\right\rfloor,\quad x_{\text{red}}=x-3\,k(x)\in[0,3),\quad f(x)=f\bigl(x_{\text{red}}\bigr).$$

Здесь $\lfloor\cdot\rfloor$ — «пол» (целая часть вниз). Эта формула корректно работает и для отрицательных $x$.

а) Построение на отрезке $[3;6]$

Это ровно один период вправо от базового куска: $[3;6]=[0;3]+3$.

Как рисовать:

1. Возьмите видимый на рисунке фрагмент на $[0;3]$.
2. Сдвиньте вправо на 3: каждую точку $(x,y)$ замените на $(x+3,y)$.
3. Получите копию графика на $[3;6]$.

Формула соответствия точек:

$$x\in[3,6]\ \Rightarrow\ f(x)=f(x-3),\quad x-3\in[0,3].$$

Практически: нули, вершины, изломы из точек $x=x_0\in[0,3]$ повторятся в $x=x_0+3$.

б) Построение на отрезке $[-3;0]$

Это один период влево: $[-3;0]=[0;3]-3$.

Как рисовать:

1. Возьмите фрагмент $[0;3]$.
2. Сдвиньте его влево на 3: $(x,y)\mapsto(x-3,y)$.
3. Получите копию на $[-3;0]$.

Формула соответствия:

$$x\in[-3,0]\ \Rightarrow\ f(x)=f(x+3),\quad x+3\in[0,3].$$

Все характерные точки $x_0\in[0,3]$ переедут в $x_0-3$.

в) Построение на отрезке $[6;12]$

Длина $[6;12]$ равна $6$, это два полных периода. Удобно разбить:

• $[6;9]=[0;3]+6$ — сдвиг на $+6$ (два периода),
• $[9;12]=[0;3]+9$ — сдвиг на $+9$ (три периода).

Как рисовать:

1. Скопируйте базовый кусок $[0;3]$ и сдвиньте вправо на 6 → получите участок на $[6;9]$.
2. Ещё раз скопируйте $[0;3]$ и сдвиньте вправо на 9 → получите участок на $[9;12]$.
3. Соедините их подряд — получится график на всём $[6;12]$.

Формулы соответствия:

$$\begin{aligned} &x\in[6,9]\ \Rightarrow\ f(x)=f(x-6),\quad x-6\in[0,3],\\ &x\in[9,12]\ \Rightarrow\ f(x)=f(x-9),\quad x-9\in[0,3]. \end{aligned}$$

г) Построение на всей числовой прямой

Весь график — это повторение куска $[0;3]$ со сдвигом на $\,3k$ для всех целых $k$:

$$\text{График }y=f(x)\text{ на }\mathbb{R} =\bigcup_{k\in\mathbb{Z}}\ \{(x+3k,\ f(x)):\ x\in[0,3]\}.$$

Эквивалентный алгоритм для любой точки $x$:

1. Найдите $k=\left\lfloor \dfrac{x}{3}\right\rfloor$.
2. Верните аргумент в базовый интервал: $x_{\text{red}}=x-3k\in[0,3)$.
3. Поставьте $f(x)=f(x_{\text{red}})$ и отмечайте на графике ту же высоту $y$, что и в точке $x_{\text{red}}$ на исходном рисунке.

Полезные техники для аккуратного чертежа

• Стыки периодов находятся в точках $x=3k$ ($\ldots,-6,-3,0,3,6,9,12,\ldots$). Ровно те же типы особенностей (разрывы, вершины, углы), что в $x=0$ и $x=3$, появятся в каждом таком $x$.
• Передача ключевых точек. Если на $[0,3]$ есть, например, нуль $x=a$, максимум $x=m$, излом $x=c$, то они повторяются в $x=a+3k$, $x=m+3k$, $x=c+3k$ при всех целых $k$.
• Высоты $y$ не меняются — выполняются только горизонтальные сдвиги.
• Границы интервалов. Чтобы не утолщать линию на стыках, рисуйте копии как $[0,3)$, $[3,6)$, $[6,9)$, $\ldots$ (левая включена, правая нет). Это избавляет от «двойного» прорисовывания одной и той же точки.