ГДЗ 10-11 Класс Номер 12.3 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

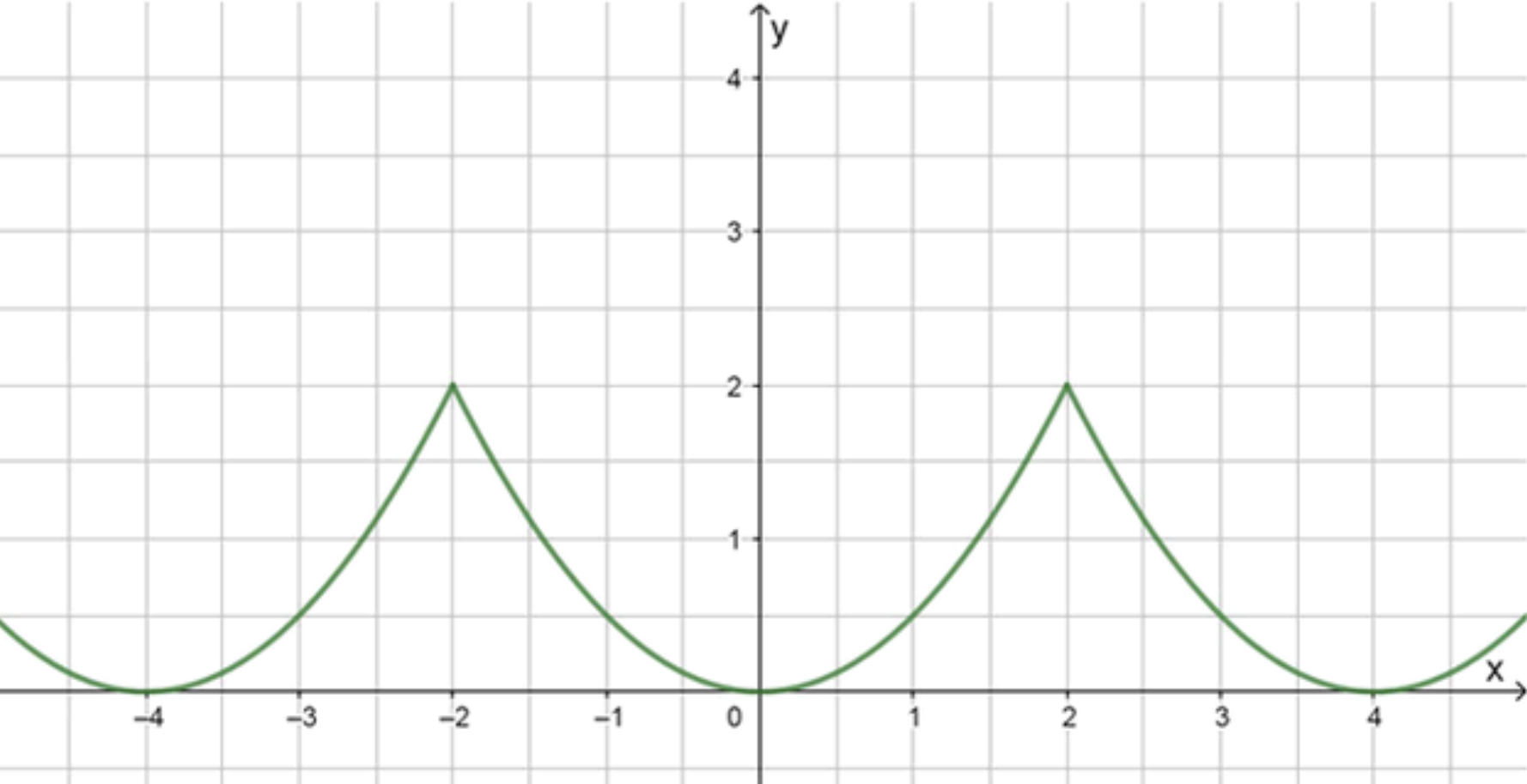
Постройте график периодической функции у = f(х) с периодом Т = 4, если известно, что f(x) = $\frac{x^2}{2}$ на отрезке [-2; 2].

Известно, что $f(x) = \frac{x^2}{2}$ на отрезке $[-2; 2]$ и $T = 4$;

Дано уравнение параболы:
$x_0 = 0, \quad y_0 = 0;$

График функции:

Дано:

• Функция $f(x) = \frac{x^2}{2}$ на отрезке $[-2; 2]$.
• Период функции $T = 4$.

Шаг 1: Общее представление о функции

Функция $f(x) = \frac{x^2}{2}$ на отрезке $[-2; 2]$ — это парабола с вершиной в точке $(0, 0)$, и она имеет форму $y = \frac{x^2}{2}$, то есть растёт по обеим сторонам от $x = 0$. Например, для $x = 1$ $y = \frac{1^2}{2} = 0.5$, а для $x = 2$ $y = \frac{2^2}{2} = 2$.

Так как $T = 4$, это означает, что функция будет периодической с периодом 4, то есть она повторяется каждые 4 единицы по оси $x$.

Шаг 2: Определение поведения функции на других отрезках

Так как период функции $T = 4$, она будет повторять свою форму на всех интервалах с шагом в 4 единицы. Это означает, что функция будет одинаково выглядеть на следующих интервалах:

• $[-2, 2]$,
• $[2, 6]$,
• $[6, 10]$,
• $[-6, -2]$,
• и так далее.

Для построения графика важно понимать, что на интервалах $[2, 6]$, $[6, 10]$ и других таких интервалах, функция будет повторять вид параболы на отрезке $[-2; 2]$, только сдвинутый по оси $x$ на соответствующее количество периодов.

Шаг 3: Построение графика функции

На отрезке $[-2, 2]$:
Это базовый отрезок. На нём функция выглядит как парабола:

$$f(x) = \frac{x^2}{2}, \quad x \in [-2, 2].$$

Для нескольких ключевых точек:

• $f(-2) = \frac{(-2)^2}{2} = 2$,
• $f(0) = \frac{0^2}{2} = 0$,
• $f(2) = \frac{2^2}{2} = 2$.

Это стандартная парабола, открывающаяся вверх.

На отрезке $[2, 6]$:
Это следующий период функции. Здесь график будет идентичным, но сдвинут на 4 единицы вправо, то есть на интервале $[2, 6]$ функция будет такой же, как и на $[-2, 2]$, но сдвинута вправо на 4 единицы:

$$f(x) = \frac{(x — 4)^2}{2}, \quad x \in [2, 6].$$

Таким образом, для нескольких точек:

• $f(2) = 2$,
• $f(4) = \frac{(4)^2}{2} = 8$,
• $f(6) = \frac{(6 — 4)^2}{2} = 2$.

На отрезке $[6, 10]$:
Для следующего периода, аналогично предыдущим, график повторяет базовую параболу сдвинутую на 8 единиц вправо:

$$f(x) = \frac{(x — 8)^2}{2}, \quad x \in [6, 10].$$

И так далее для всех последующих периодов.

На отрезке $[-6, -2]$:
На этом интервале график будет повторять форму параболы на отрезке $[-2, 2]$, но сдвинут влево на 4 единицы:

$$f(x) = \frac{(x + 4)^2}{2}, \quad x \in [-6, -2].$$

Шаг 4: Общая формула для периодической функции

Так как функция периодическая с периодом $T = 4$, мы можем записать её для любого $x$ следующим образом:

$$f(x) = \frac{(x — 4k)^2}{2}, \quad x \in [-2, 2] + 4k, \quad k \in \mathbb{Z}.$$

Здесь $k$ — это целое число, которое отвечает за количество периодов. Функция будет повторяться через каждый интервал длиной $4$.

Шаг 5: Построение графика

Чтобы построить график, нужно отрисовать параболу на интервале $[-2; 2]$, а затем повторить её на других интервалах с шагом 4:

• На отрезке $[-2; 2]$ парабола имеет вершину в точке $(0, 0)$, и значения $f(x) = \frac{x^2}{2}$.
• На отрезке $[2; 6]$ парабола будет сдвинута на 4 единицы вправо, то есть её вершина будет в точке $(4, 0)$, и она будет иметь форму $f(x) = \frac{(x — 4)^2}{2}$.
• На отрезке $[6; 10]$ — сдвиг ещё на 4 единицы вправо, вершина в точке $(8, 0)$, и так далее.