ГДЗ 10-11 Класс Номер 12.4 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

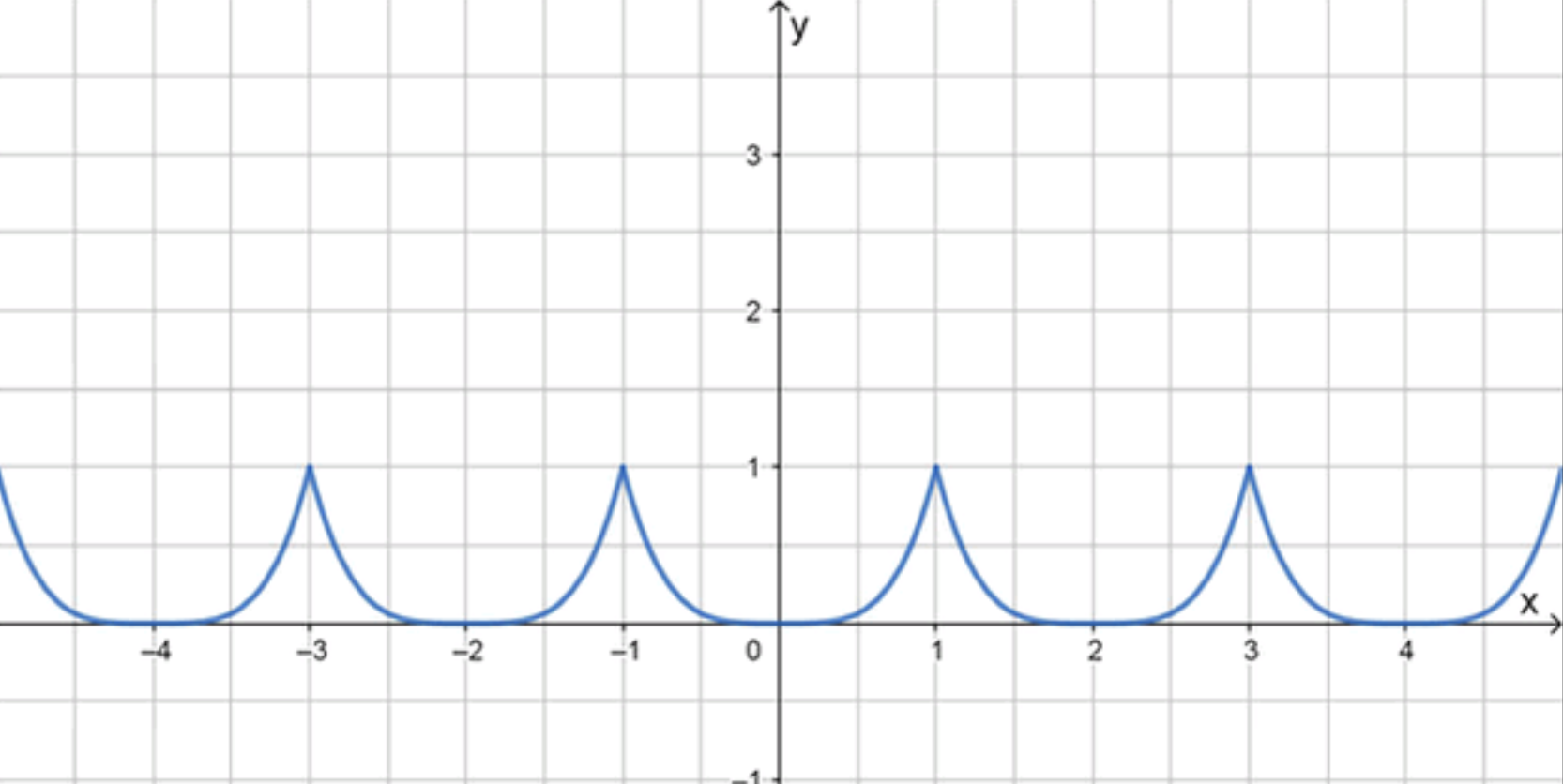
Постройте график периодической функции у = f(x) с периодом Т = 2, если известно, что f(x) = $x^4$ на отрезке [-1; 1]

Известно, что $f(x) = x^4$ на отрезке $[-1; 1]$ и $T = 2$;

Дано уравнение параболы:
$x_0 = 0, \quad y_0 = 0;$

$$\begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline y & -1 & 1 \\ \hline \end{array}$$

График функции:

Чтобы построить график периодической функции $y = f(x)$ с периодом $T = 2$, если известно, что на отрезке $[-1; 1]$ $f(x) = x^4$, давайте рассмотрим задачу поэтапно с детальной проработкой.

Шаг 1: Описание функции

Дана функция $f(x) = x^4$ на отрезке $[-1; 1]$. Это стандартная функция, которая при $x = 0$ имеет значение $f(0) = 0$, при $x = \pm 1$ — значение $f(\pm 1) = 1$. Функция $f(x) = x^4$ является чётной, то есть $f(x) = f(-x)$, и для всех $x$ на отрезке $[-1; 1]$ функция всегда положительна или равна нулю, достигая минимального значения в точке $x = 0$.

Ключевые значения на интервале $[-1; 1]$:

• $f(-1) = 1$,
• $f(0) = 0$,
• $f(1) = 1$.

График функции на этом интервале будет выглядеть как «парабола» (гладкая кривая) с вершиной в точке $(0, 0)$ и максимальными значениями в точках $(-1, 1)$ и $(1, 1)$.

Шаг 2: Периодическая функция

Функция имеет период $T = 2$, это означает, что её график повторяется каждые 2 единицы вдоль оси $x$.

Важное замечание: так как период равен $2$, то на каждом интервале длины $2$, например, на интервале $[1; 3]$, функция будет выглядеть точно так же, как на отрезке $[-1; 1]$, но сдвинутая вправо на 2 единицы. То же самое произойдёт и на всех последующих интервалах.

Таким образом, мы можем записать, что для всех $x \in \mathbb{R}$:

$$f(x + 2k) = f(x), \quad k \in \mathbb{Z}.$$

Это означает, что график функции будет повторяться на интервалах $[2k — 1, 2k + 1]$, где $k \in \mathbb{Z}$, и на каждом таком интервале будет иметь тот же вид, что и на интервале $[-1, 1]$.

Шаг 3: Построение графика

1. На отрезке $[-1; 1]$:

Здесь функция задана как $f(x) = x^4$, и её график будет выглядеть следующим образом:

• $f(-1) = 1$,
• $f(0) = 0$,
• $f(1) = 1$.

На интервале $[-1; 1]$ график будет гладкой параболой, с минимумом в точке $x = 0$.

2. На отрезке $[1; 3]$:

На этом интервале график функции будет повторением графика на отрезке $[-1; 1]$, но сдвинутым на 2 единицы вправо. То есть функция будет такой же, как и на интервале $[-1; 1]$, только сдвинутая вправо:

$$f(x) = (x — 2)^4, \quad x \in [1, 3].$$

Для некоторых точек:

• $f(1) = 1$,
• $f(2) = 0$,
• $f(3) = 1$.

График будет иметь тот же вид, что и на отрезке $[-1; 1]$, с точками симметрии относительно $x = 2$.

3. На отрезке $[3; 5]$:

Здесь график функции будет сдвинут ещё на 2 единицы вправо:

$$f(x) = (x — 4)^4, \quad x \in [3, 5].$$

Для некоторых точек:

• $f(3) = 1$,
• $f(4) = 0$,
• $f(5) = 1$.

Этот график будет идентичен предыдущим, но сдвинут ещё правее.

4. На отрезке $[-3; -1]$:

Для отрезков слева от нуля график будет зеркально симметричен графику на отрезке $[0; 2]$. Он будет повторять тот же вид, только сдвинут на 2 единицы влево:

$$f(x) = (x + 2)^4, \quad x \in [-3, -1].$$

Для точек:

• $f(-3) = 1$,
• $f(-2) = 0$,
• $f(-1) = 1$.

5. Общая формула для всех отрезков:

График функции будет повторяться с периодом 2, то есть для любого $x$ функция будет иметь вид:

$$f(x) = (x — 2k)^4, \quad x \in [-1 + 2k, 1 + 2k], \quad k \in \mathbb{Z}.$$

Шаг 4: Построение графика на всей числовой прямой

График функции будет состоять из последовательных парабол, повторяющихся через каждые 2 единицы по оси $x$. Каждая парабола будет выглядеть одинаково на интервалах $[-1 + 2k, 1 + 2k]$, $k \in \mathbb{Z}$, и будет иметь вид:

• Вершина в точке $(2k, 0)$,
• Максимумы в точках $(-1 + 2k, 1)$ и $(1 + 2k, 1)$.

График будет состоять из последовательных «парабол», каждая из которых будет начинаться в точке $(-1 + 2k, 1)$, проходить через точку $(2k, 0)$, и заканчиваться в точке $(1 + 2k, 1)$.