ГДЗ 10-11 Класс Номер 13.10 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \sin \frac{x}{3}$;

б) $y = \cos 2x$;

в) $y = \cos \frac{x}{2}$;

г) $y = \sin 3x$

Построить график функции:

а) $y = \sin \frac{x}{3}$;

Построим дугу графика $y = \sin x$;

Растянем ее в 3 раза от оси ординат;

Достроим график функции:

б) $y = \cos 2x$;

Построим дугу графика $y = \cos x$;

Сожмем ее в 2 раза к оси ординат;

Достроим график функции:

в) $y = \cos \frac{x}{2}$;

Построим дугу графика $y = \cos x$;

Растянем ее в 2 раза от оси ординат;

Достроим график функции:

г) $y = \sin 3x$;

Построим дугу графика $y = \sin x$;

Сожмем ее в 3 раза к оси ординат;

Достроим график функции:

а) $y = \sin \frac{x}{3}$

Шаги построения графика:

Исходная функция: $y = \sin x$.

• График функции $y = \sin x$ — это стандартная синусоида с амплитудой 1 и периодом $2\pi$. График колеблется между значениями $-1$ и $1$, период равен $2\pi$, и он начинается в точке $(0, 0)$.

Преобразование: $y = \sin \frac{x}{3}$

• В данной функции $\frac{x}{3}$ является изменением аргумента синуса. Это растяжение графика вдоль оси абсцисс.
• Чтобы понять, как это изменение влияет на график, нужно рассмотреть период функции. Обычно период функции $y = \sin x$ равен $2\pi$. Однако в случае $y = \sin \frac{x}{3}$, период изменится, потому что аргумент $\frac{x}{3}$ растягивает график.
• Новый период $T$ будет:

  $$T = 2\pi \cdot 3 = 6\pi$$

• Таким образом, график функции $y = \sin \frac{x}{3}$ будет растянут в 3 раза по оси $x$, и его период составит $6\pi$, а амплитуда останется 1.

График:

• График функции будет колебаться между значениями $-1$ и $1$, но будет иметь больший период — $6\pi$ вместо $2\pi$. Он будет начинаться в точке $(0, 0)$, проходить через максимальные и минимальные точки в течение одного полного периода и повторять этот процесс.

Ответ: График функции будет синусоидой с периодом $6\pi$, начинающейся в точке $(0, 0)$ и колеблющейся между $-1$ и $1$.

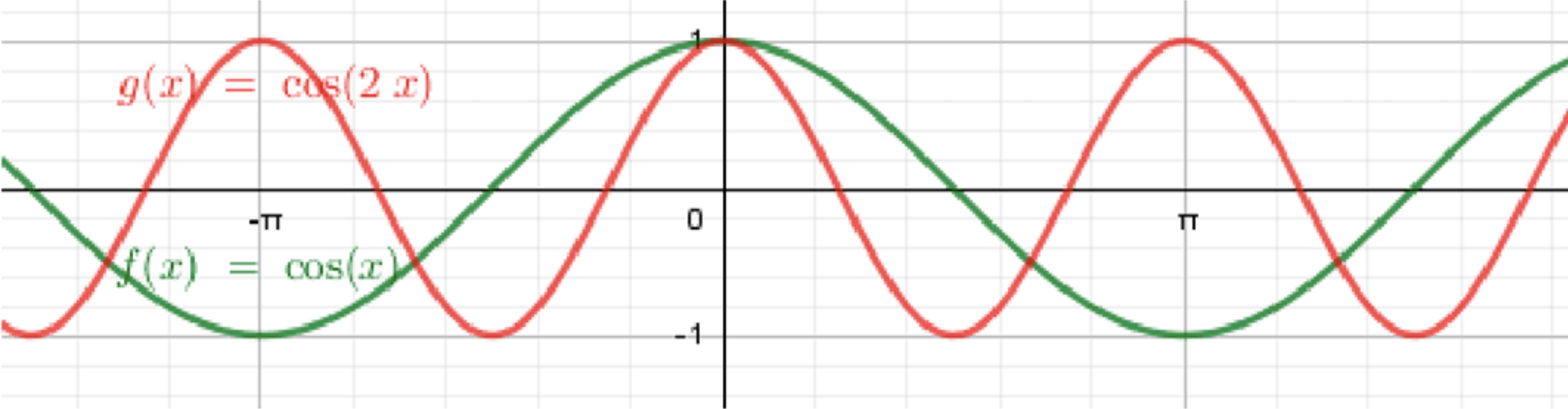
б) $y = \cos 2x$

Шаги построения графика:

Исходная функция: $y = \cos x$.

• График функции $y = \cos x$ — это стандартная косинусоида с амплитудой 1 и периодом $2\pi$. График колеблется между значениями $-1$ и $1$, и период составляет $2\pi$.

Преобразование: $y = \cos 2x$

• Здесь происходит сжатие графика по оси абсцисс. Умножение аргумента на 2 сжимает период функции.
• Новый период $T$ будет:

  $$T = \frac{2\pi}{2} = \pi$$

• То есть, график функции $y = \cos 2x$ будет колебаться дважды за один период $2\pi$, и его период составит $\pi$.

График:

• График функции $y = \cos 2x$ будет колебаться между значениями $-1$ и $1$, но его период будет в два раза меньше, чем у стандартной косинусоиды. Он будет совершать два полных колебания за один период $2\pi$.

Ответ: График функции будет косинусоидой с периодом $\pi$, начинающейся в точке $(0, 1)$ и совершая два полных колебания за $2\pi$.

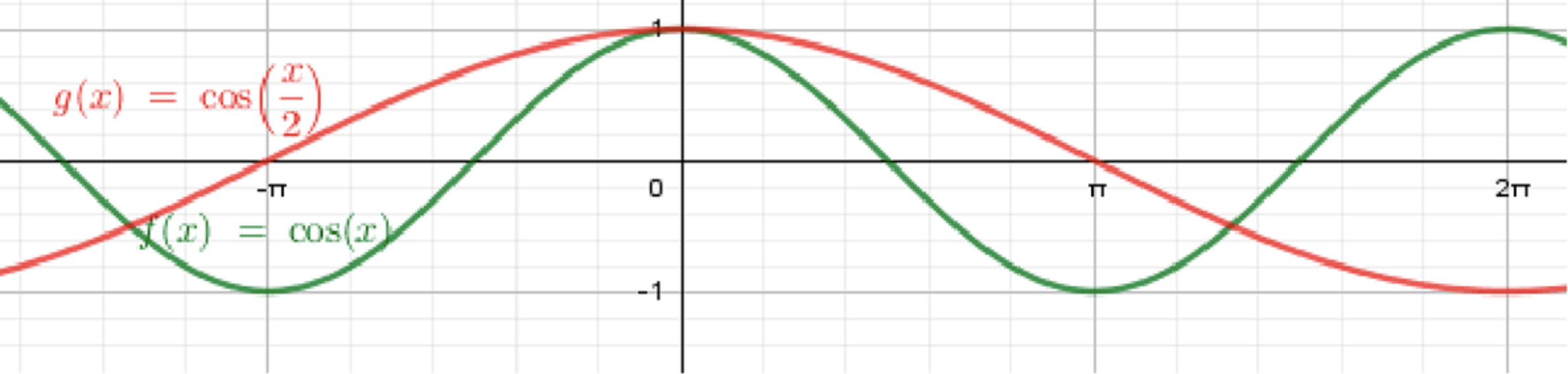
в) $y = \cos \frac{x}{2}$

Шаги построения графика:

Исходная функция: $y = \cos x$.

• График функции $y = \cos x$ — это стандартная косинусоида с амплитудой 1 и периодом $2\pi$.

Преобразование: $y = \cos \frac{x}{2}$

• В этой функции $\frac{x}{2}$ является изменением аргумента косинуса. Это растяжение графика вдоль оси абсцисс.
• Новый период $T$ будет:

  $$T = 2\pi \cdot 2 = 4\pi$$

• Таким образом, график функции $y = \cos \frac{x}{2}$ будет растянут по оси $x$ в 2 раза, и его период составит $4\pi$.

График:

• График будет колебаться между значениями $-1$ и $1$, но его период будет в два раза больше, чем у стандартной косинусоиды, и составит $4\pi$. Он будет начинаться в точке $(0, 1)$ и совершать одно полное колебание за период $4\pi$.

Ответ: График функции будет косинусоидой с периодом $4\pi$, начинающейся в точке $(0, 1)$ и колеблющейся между $-1$ и $1$.

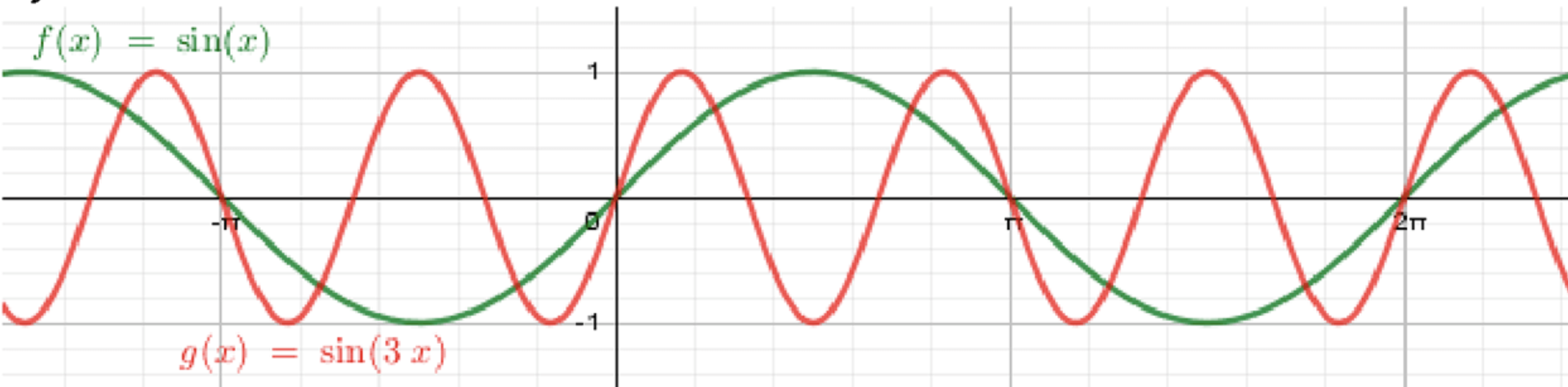
г) $y = \sin 3x$

Шаги построения графика:

Исходная функция: $y = \sin x$.

• График функции $y = \sin x$ — это стандартная синусоида с амплитудой 1 и периодом $2\pi$.

Преобразование: $y = \sin 3x$

• Здесь происходит сжатие графика по оси абсцисс. Умножение аргумента на 3 сжимает период функции.
• Новый период $T$ будет:

  $$T = \frac{2\pi}{3}$$

• То есть, график функции $y = \sin 3x$ будет колебаться трижды за один период $2\pi$, и его период составит $\frac{2\pi}{3}$.

График:

• График функции $y = \sin 3x$ будет колебаться между значениями $-1$ и $1$, но его период будет в три раза меньше, чем у стандартной синусоиды. Он будет совершать три полных колебания за один период $2\pi$.

Ответ: График функции будет синусоидой с периодом $\frac{2\pi}{3}$, начиная с точки $(0, 0)$ и совершая три полных колебания за $2\pi$.