ГДЗ 10-11 Класс Номер 13.18 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте и прочитайте график функции у = f(x):

а) $y = \begin{cases} \cos 2x, & \text{если } x \leq \pi \\ -\frac{1}{2}, & \text{если } x > \pi \end{cases}$;

б) $y = \begin{cases} -\sin 3x, & \text{если } x < 0 \\ \sqrt{x}, & \text{если } x \geq 0 \end{cases}$

Построить и прочитать график функции $y = f(x)$:

В данной задаче $n$ — целое неотрицательное число;

а) $y = \begin{cases} \cos 2x, & \text{если } x \leq \pi \\ -\frac{1}{2}, & \text{если } x > \pi \end{cases}$;

$y = \cos 2x$ — уравнение синусоиды:
$y(\pi) = \cos 2\pi = 1$;

$y = -\frac{1}{2}$ — уравнение прямой;

График функции:

Свойства функции:

• $D(f) = (-\infty; +\infty)$; $E(f) = [-1; 1]$;
• Возрастает на $\left[\frac{\pi}{2} — 2\pi n; \pi — 2\pi n\right]$;
• Убывает на $\left[-2\pi n; \frac{\pi}{2} — 2\pi n\right]$;
• Постоянна на $(\pi; +\infty)$;
• $f(x) > 0$ на $\left(-\frac{\pi}{4} — 2\pi n; \frac{\pi}{4} — 2\pi n\right) \cup \left(\frac{3\pi}{4}; \pi\right]$;
• $f(x) < 0$ на $\left(\frac{\pi}{4} — 2\pi n; \frac{3\pi}{4} — 2\pi n\right) \cup (\pi; +\infty)$;
• Ограничена снизу и сверху;
• $y_{\text{наим}} = y\left(\frac{\pi}{2}\right) = -1$;
• $y_{\text{наиб}} = y(0) = 1$;
• Ни четная, ни нечетная;
• Не является периодической;
• Непрерывна на $(-\infty; \pi) \cup (\pi; +\infty)$;

б) $y = \begin{cases} -\sin 3x, & \text{если } x < 0 \\ \sqrt{x}, & \text{если } x \geq 0 \end{cases}$;

$y = -\sin 3x$ — уравнение синусоиды:
$y(0) = -\sin (3 \cdot 0) = -\sin 0 = 0$;

$y = \sqrt{x}$ — уравнение ветви параболы:
$x_0 = 0$, $y_0 = 0$;

График функции:

Свойства функции:

• $D(f) = (-\infty; +\infty)$; $E(f) = [-1; +\infty)$;
• Возрастает на $\left[-\frac{\pi}{2} — 2\pi n; -\frac{\pi}{6} — 2\pi n\right] \cup [0; +\infty)$;
• Убывает на $\left[-\frac{5\pi}{6} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right] \cup \left[-\frac{\pi}{6}; 0\right]$;
• $f(x) > 0$ на $\left(-\frac{\pi}{3} — 2\pi n; -2\pi n\right) \cup (0; +\infty)$;
• $f(x) < 0$ на $\left(-\frac{2\pi}{3} — 2\pi n; -\frac{\pi}{3} — 2\pi n\right)$;
• Ограничена снизу;
• $y_{\text{наим}} = y\left(-\frac{\pi}{2}\right) = -1$;
• Ни четная, ни нечетная;
• Не является периодической;
• Непрерывна на $(-\mathrm{\infty };+\mathrm{\infty })$

Построить и прочитать график функции $y = f(x)$.

В данной задаче $n$ — целое неотрицательное число.

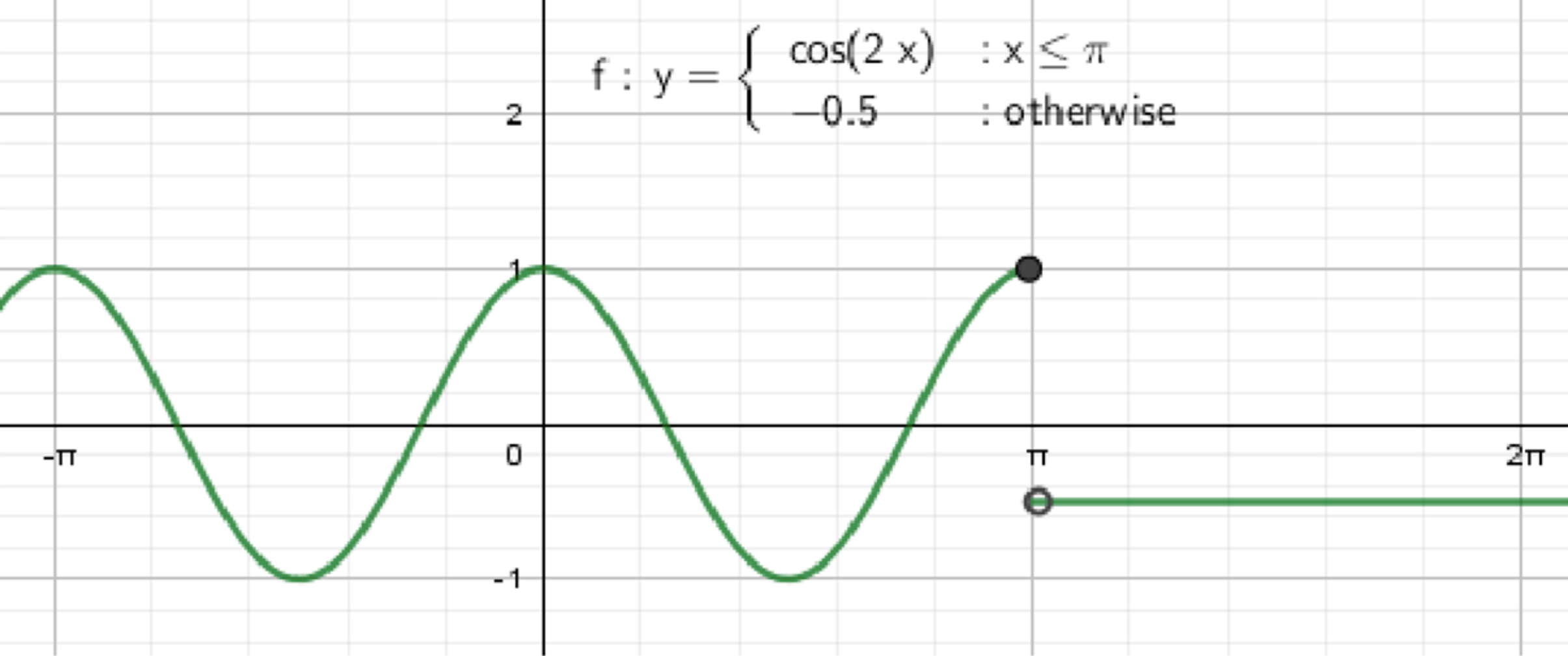
Часть а)

Функция представлена в виде:

$$y = \begin{cases} \cos 2x, & \text{если } x \leq \pi \\ -\frac{1}{2}, & \text{если } x > \pi \end{cases}$$

Здесь дано два разных выражения для функции: $y = \cos 2x$ для $x \leq \pi$ и $y = -\frac{1}{2}$ для $x > \pi$.

1. График функции $y = \cos 2x$ на интервале $(-\infty; \pi]$:

Это уравнение синусоиды, которая имеет период $\frac{\pi}{2}$, так как аргумент $2x$ удваивает период стандартной косинусоиды. Период $T = \frac{2\pi}{2} = \pi$, то есть функция будет повторяться через каждые $\pi$ единиц.

1.1. В точке $x = \pi$:

$$y(\pi) = \cos(2\pi) = 1$$

Это максимальное значение функции на этом интервале.

1.2. В точке $x = 0$:

$$y(0) = \cos(0) = 1$$

Это тоже максимальное значение функции.

1.3. В точке $x = \frac{\pi}{2}$:

$$y\left(\frac{\pi}{2}\right) = \cos(\pi) = -1$$

Это минимальное значение функции на этом интервале.

1.4. Функция $y = \cos 2x$ будет колебаться между $-1$ и $1$, при этом функция будет убывать на интервале $\left(0; \frac{\pi}{2}\right)$ и возрастать на интервале $\left(\frac{\pi}{2}; \pi\right)$.

2. График функции $y = -\frac{1}{2}$ для $x > \pi$:

Это уравнение прямой, которая постоянна и равна $-\frac{1}{2}$ для всех значений $x$, больших $\pi$. График этой части функции будет горизонтальной линией, расположенной на уровне $y = -\frac{1}{2}$.

3. Общий вид графика:

График функции будет выглядеть следующим образом:

• На интервале $(-\infty; \pi]$ функция будет следовать за графиком синусоиды $y = \cos 2x$.
• На интервале $(\pi; +\infty)$ функция будет постоянной и равной $-\frac{1}{2}$.

4. Свойства функции:

• Область определения $D(f) = (-\infty; +\infty)$, так как функция определена для всех $x$.
• Множество значений $E(f) = [-1; 1]$, так как функция колеблется от $-1$ до $1$ для $x \leq \pi$, а для $x > \pi$ принимает значение $-\frac{1}{2}$, которое лежит в этом интервале.
• Функция возрастает на интервале $\left[\frac{\pi}{2} — 2\pi n; \pi — 2\pi n\right]$, так как на этом интервале косинусная функция возрастает.
• Функция убывает на интервале $\left[-2\pi n; \frac{\pi}{2} — 2\pi n\right]$, так как на этом интервале косинусная функция убывает.
• Функция постоянна на интервале $(\pi; +\infty)$, так как для $x > \pi$ функция принимает постоянное значение $-\frac{1}{2}$.
• Функция $f(x) > 0$ на интервале $\left(-\frac{\pi}{4} — 2\pi n; \frac{\pi}{4} — 2\pi n\right) \cup \left(\frac{3\pi}{4}; \pi\right]$, так как косинус в этих интервалах положителен.
• Функция $f(x) < 0$ на интервале $\left(\frac{\pi}{4} — 2\pi n; \frac{3\pi}{4} — 2\pi n\right) \cup (\pi; +\infty)$, так как косинус в этих интервалах отрицателен.
• Функция ограничена снизу и сверху, так как её значения находятся в пределах от $-1$ до $1$, и значение $-\frac{1}{2}$ для $x > \pi$ также лежит в этом диапазоне.
• Наименьшее значение функции $y_{\text{наим}} = y\left(\frac{\pi}{2}\right) = -1$, так как это минимум косинусоиды.
• Наибольшее значение функции $y_{\text{наиб}} = y(0) = 1$, так как это максимум косинусоиды.
• Функция не является чётной или нечётной, так как она не симметрична относительно оси $y$ или относительно начала координат.
• Функция не является периодической, так как на интервале $(\pi; +\infty)$ она становится постоянной, что нарушает периодичность.
• Функция непрерывна на $(-\infty; \pi) \cup (\pi; +\infty)$, так как для $x = \pi$ происходят скачки в значении функции (с $\cos 2x$ на $-\frac{1}{2}$), но она не имеет разрывов в области определения.

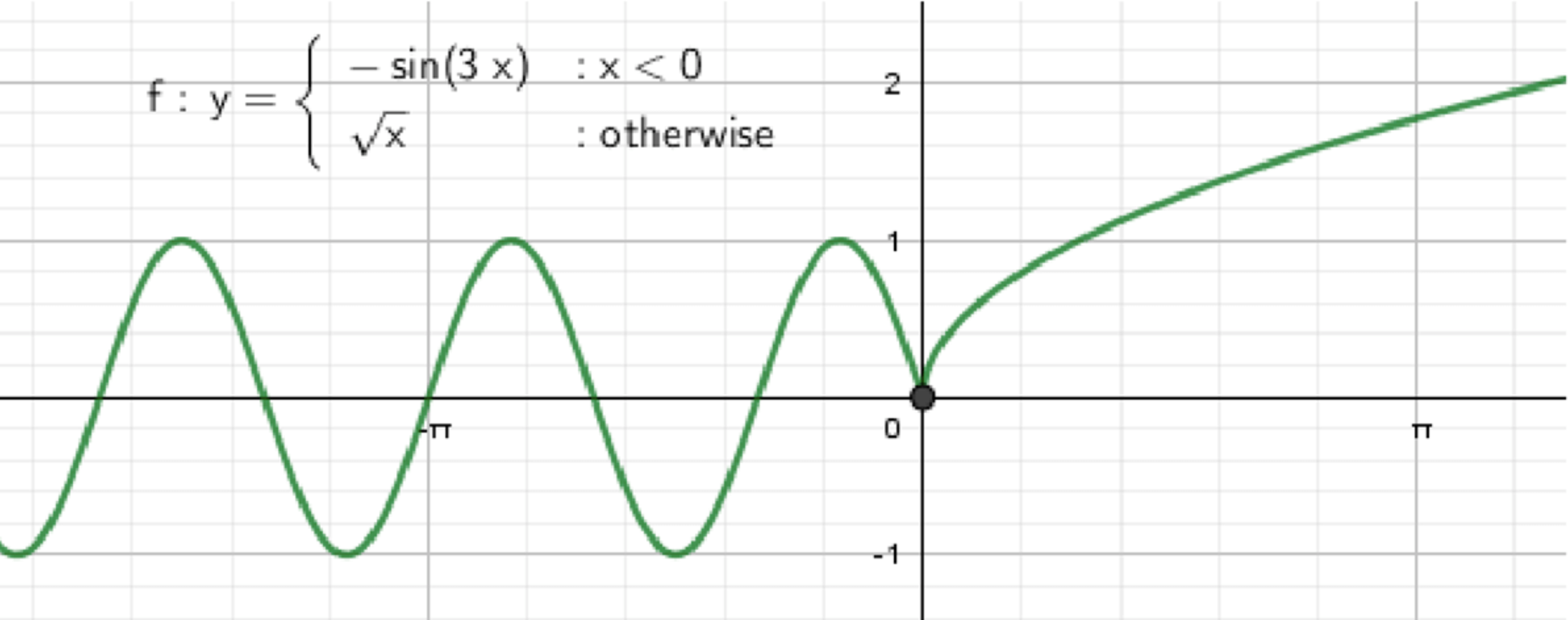
Часть б)

Функция представлена в виде:

$$y = \begin{cases} -\sin 3x, & \text{если } x < 0 \\ \sqrt{x}, & \text{если } x \geq 0 \end{cases}$$

1. График функции $y = -\sin 3x$ для $x < 0$:

Это уравнение синусоиды с коэффициентом $3$ перед $x$, который уменьшает её период. Период функции $y = -\sin 3x$ равен:

$$T = \frac{2\pi}{3}$$

То есть функция будет повторяться через $\frac{2\pi}{3}$ единиц.

1.1. В точке $x = 0$:

$$y(0) = -\sin(0) = 0$$

1.2. В точке $x = -\frac{\pi}{6}$:

$$y\left(-\frac{\pi}{6}\right) = -\sin\left(-\frac{\pi}{2}\right) = 1$$

1.3. В точке $x = -\frac{\pi}{2}$:

$$y\left(-\frac{\pi}{2}\right) = -\sin\left(-\frac{3\pi}{2}\right) = -1$$

Таким образом, для $x < 0$ график будет представлять собой синусоиду с периодом $\frac{2\pi}{3}$, и будет колебаться между $-1$ и $1$.

2. График функции $y = \sqrt{x}$ для $x \geq 0$:

Это уравнение ветви параболы, начинающееся в точке $(0, 0)$. Функция определена только для $x \geq 0$, и её график будет монотонно возрастать.

2.1. В точке $x = 0$:

$$y(0) = \sqrt{0} = 0$$

2.2. В точке $x = 1$:

$$y(1) = \sqrt{1} = 1$$

2.3. В точке $x = 4$:

$$y(4) = \sqrt{4} = 2$$

График этой функции — это возрастающая кривая, которая будет проходить через точки $(0, 0)$, $(1, 1)$, $(4, 2)$, и так далее.

3. Общий вид графика:

График функции будет состоять из двух частей:

• Для $x < 0$ график будет представлять собой синусоиду $y = -\sin 3x$.
• Для $x \geq 0$ график будет представлять собой ветвь параболы $y = \sqrt{x}$.

4. Свойства функции:

• Область определения $D(f) = (-\infty; +\infty)$, так как функция определена для всех $x$.
• Множество значений $E(f) = [-1; +\infty)$, так как значения функции для $x < 0$ колеблются между $-1$ и $1$, а для $x \geq 0$ функция принимает значения от 0 до $+\infty$.
• Функция возрастает на интервале $\left[-\frac{\pi}{2} — 2\pi n; -\frac{\pi}{6} — 2\pi n\right] \cup [0; +\infty)$.
• Функция убывает на интервале $\left[-\frac{5\pi}{6} — 2\pi n; -\frac{\pi}{2} — 2\pi n\right] \cup \left[-\frac{\pi}{6}; 0\right]$.
• Функция $f(x) > 0$ на $\left(-\frac{\pi}{3} — 2\pi n; -2\pi n\right) \cup (0; +\infty)$.
• Функция $f(x) < 0$ на $\left(-\frac{2\pi}{3} — 2\pi n; -\frac{\pi}{3} — 2\pi n\right)$.
• Функция ограничена снизу, так как $\sqrt{x}$ не может быть отрицательным, а синусоидальная часть колеблется между $-1$ и $1$.
• Наименьшее значение функции $y_{\text{наим}} = y\left(-\frac{\pi}{2}\right) = -1$.
• Функция не является чётной или нечётной, так как она не симметрична относительно оси $y$ или начала координат.
• Функция не является периодической, так как на интервале $[0; +\infty)$ она монотонно возрастает.
• Функция непрерывна на $(-\infty; +\infty)$.