ГДЗ 10-11 Класс Номер 13.2 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

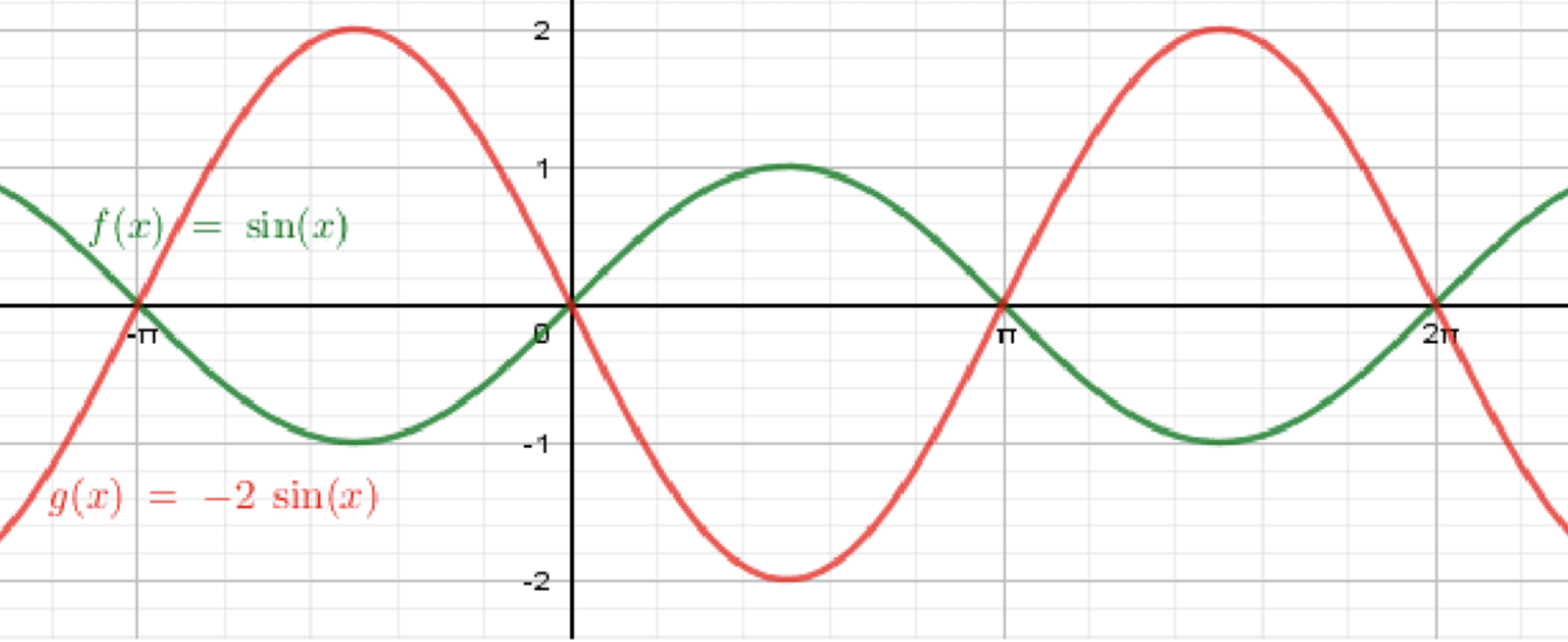
a) y = -2sinx;

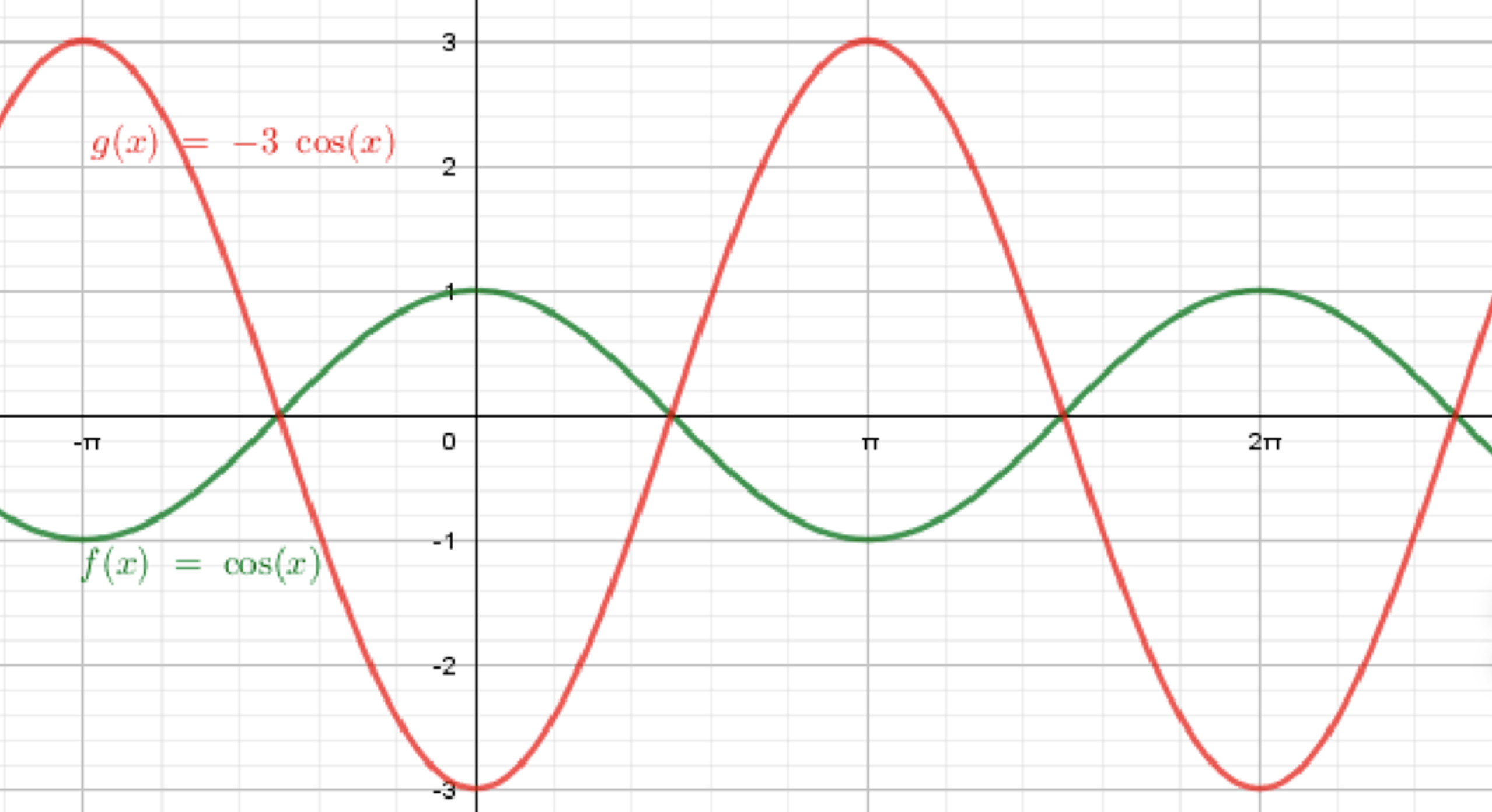
б) y = -3cosx;

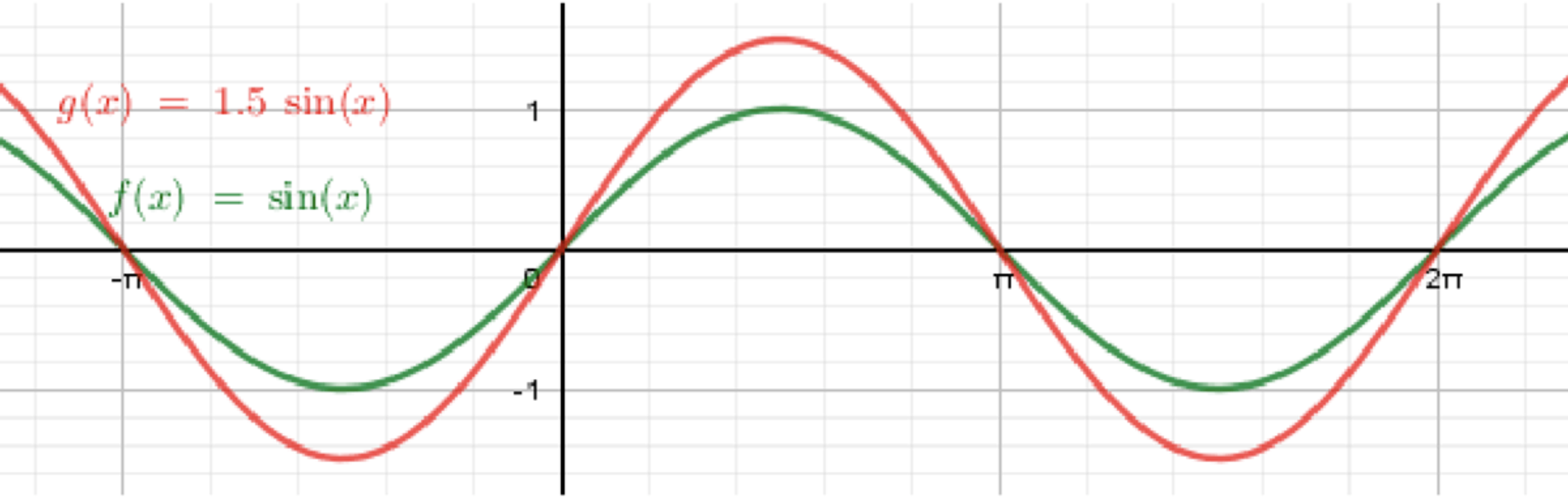
в) y = 1,5sinx;

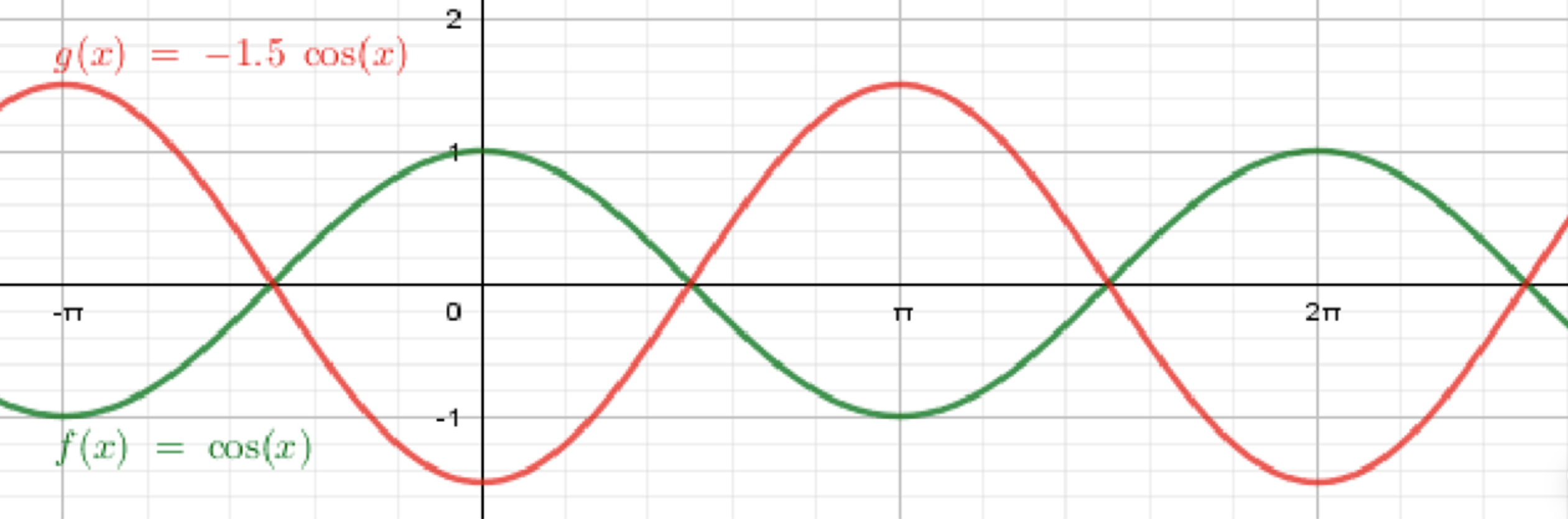
г) y = -1,5cosx.

Построить график функции:

а) $y = -2 \sin x$;

• Построим график функции $y = \sin x$;
• Отразим его относительно оси абсцисс;
• Растянем его в 2 раза от оси абсцисс;

б) $y = -3 \cos x$;

• Построим график функции $y = \cos x$;
• Отразим его относительно оси абсцисс;
• Растянем его в 3 раза от оси абсцисс;

в) $y = 1,5 \sin x$;

• Построим график функции $y = \sin x$;
• Растянем его в 1,5 раза от оси абсцисс;

г) $y = -1,5 \cos x$;

• Построим график функции $y = \cos x$;
• Отразим его относительно оси абсцисс;
• Растянем его в 1,5 раза от оси абсцисс;

а) $y = -2 \sin x$:

Рассмотрим график функции $y = \sin x$:

• Функция $y = \sin x$ является периодической с периодом $2\pi$. Она колеблется между значениями $y = -1$ и $y = 1$.
• График функции проходит через ось абсцисс в точках $x = n\pi$, где $n$ — целое число.
• Амплитуда функции $\sin x$ равна 1, то есть максимальное значение $y = 1$ и минимальное значение $y = -1$.

Отражение графика относительно оси абсцисс:

• Умножение функции на -1 приводит к отражению графика относительно оси $x$. Теперь, если $y = \sin x$ имеет значения $y$ от -1 до 1, то после отражения график будет колебаться от 1 до -1 (график будет инвертирован).
• Получаем функцию $y = -\sin x$, где график будет расположен симметрично относительно оси $x$, но с инвертированными значениями.

Растяжение графика по вертикали в 2 раза:

• Умножение функции $y = -\sin x$ на 2 приводит к растяжению графика вдоль оси $y$.
• Теперь амплитуда функции становится равной 2, то есть график будет колебаться между значениями $y = -2$ и $y = 2$.
• Период функции останется равным $2\pi$, так как растяжение по вертикали не влияет на период.

График функции $y = -2 \sin x$:

• График функции будет проходить через ось абсцисс в тех же точках, что и у функции $y = \sin x$ (то есть при $x = n\pi$).
• График будет инвертирован относительно оси $x$ и растянут в 2 раза по вертикали.
• Таким образом, график будет колебаться между значениями $y = -2$ и $y = 2$, а его период останется $2\pi$.

Итог: График функции $y = -2 \sin x$ имеет амплитуду 2 и период $2\pi$, он инвертирован относительно оси $x$ и растянут по вертикали.

б) $y = -3 \cos x$:

Рассмотрим график функции $y = \cos x$:

• Функция $y = \cos x$ является периодической с периодом $2\pi$.
• Амплитуда функции $\cos x$ равна 1, то есть график колеблется между значениями $y = -1$ и $y = 1$.
• Точки пересечения с осью абсцисс происходят при $x = \pm \frac{\pi}{2}, \pm \frac{3\pi}{2}, \dots$.

Отражение графика относительно оси абсцисс:

• Умножение функции $y = \cos x$ на -1 приводит к отражению графика относительно оси $x$.
• После отражения график функции будет колебаться от $y = -1$ до $y = 1$, но все значения будут инвертированы.

Растяжение графика по вертикали в 3 раза:

• Умножение функции $y = -\cos x$ на 3 приводит к растяжению графика по вертикали в 3 раза.
• Теперь амплитуда функции будет равна 3, то есть график будет колебаться между значениями $y = -3$ и $y = 3$.
• Период функции останется равным $2\pi$, так как растяжение не влияет на период.

График функции $y = -3 \cos x$:

• График функции будет отражен относительно оси $x$ и растянут в 3 раза по вертикали.
• Период останется равным $2\pi$, а амплитуда станет равной 3.

Итог: График функции $y = -3 \cos x$ имеет амплитуду 3 и период $2\pi$, он инвертирован относительно оси $x$ и растянут по вертикали.

в) $y = 1,5 \sin x$:

Рассмотрим график функции $y = \sin x$:

• Функция $y = \sin x$ имеет период $2\pi$ и амплитуду 1.
• График функции колеблется между значениями $y = -1$ и $y = 1$.

Растяжение графика по вертикали в 1,5 раза:

• Умножение функции $y = \sin x$ на 1,5 приводит к растяжению графика по вертикали в 1,5 раза.
• Теперь амплитуда функции становится равной 1,5, то есть график будет колебаться между значениями $y = -1,5$ и $y = 1,5$.
• Период функции останется равным $2\pi$, так как растяжение не влияет на период.

График функции $y = 1,5 \sin x$:

• График функции будет аналогичен графику функции $y = \sin x$, но растянут по вертикали в 1,5 раза.
• Период функции останется $2\pi$, а амплитуда станет равной 1,5.

Итог: График функции $y = 1,5 \sin x$ имеет амплитуду 1,5 и период $2\pi$, он растянут по вертикали.

г) $y = -1,5 \cos x$:

Рассмотрим график функции $y = \cos x$:

• Функция $y = \cos x$ имеет период $2\pi$ и амплитуду 1.
• График функции колеблется между значениями $y = -1$ и $y = 1$.

Отражение графика относительно оси абсцисс:

• Умножение функции $y = \cos x$ на -1 приводит к отражению графика относительно оси $x$.
• После отражения график будет колебаться между значениями $y = -1$ и $y = 1$, но инвертирован.

Растяжение графика по вертикали в 1,5 раза:

• Умножение функции $y = -\cos x$ на 1,5 приводит к растяжению графика по вертикали в 1,5 раза.
• Теперь амплитуда функции станет равной 1,5, то есть график будет колебаться между значениями $y = -1,5$ и $y = 1,5$.
• Период функции останется равным $2\pi$, так как растяжение не влияет на период.

График функции $y = -1,5 \cos x$:

• График функции будет отражен относительно оси $x$ и растянут по вертикали в 1,5 раза.
• Период функции останется равным $2\pi$, а амплитуда станет равной 1,5.

Итог: График функции $y = -1,5 \cos x$ имеет амплитуду 1,5 и период $2\pi$, он инвертирован относительно оси $x$ и растянут по вертикали.