ГДЗ 10-11 Класс Номер 13.20 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y=-2\cos 2(x+\frac{\pi }{3});$

б) $y=-2\sin 3(x+\frac{\pi }{2})$

Построить график функции:

а) $y = -2 \cos 2\left(x + \frac{\pi}{3}\right);$

Нули функции:

$$\cos 2\left(x + \frac{\pi}{3}\right) = 0;$$ $$2\left(x + \frac{\pi}{3}\right) = \pm \frac{\pi}{2} + 2\pi n;$$ $$x + \frac{\pi}{3} = \pm \frac{\pi}{4} + \pi n;$$ $$x_0 = -\frac{\pi}{3} — \frac{\pi}{4} = -\frac{4\pi}{12} — \frac{3\pi}{12} = -\frac{7\pi}{12};$$ $$x_1 = -\frac{\pi}{3} + \frac{\pi}{4} = -\frac{4\pi}{12} + \frac{3\pi}{12} = -\frac{\pi}{12};$$

Середина дуги:

$$x = \frac{1}{2}\left(-\frac{7\pi}{12} — \frac{\pi}{12}\right) = \frac{1}{2} \cdot \left(-\frac{2\pi}{3}\right) = -\frac{\pi}{3};$$ $$y = -2 \cos 2\left(-\frac{\pi}{3} + \frac{\pi}{3}\right) = -2 \cos 0 = -2;$$

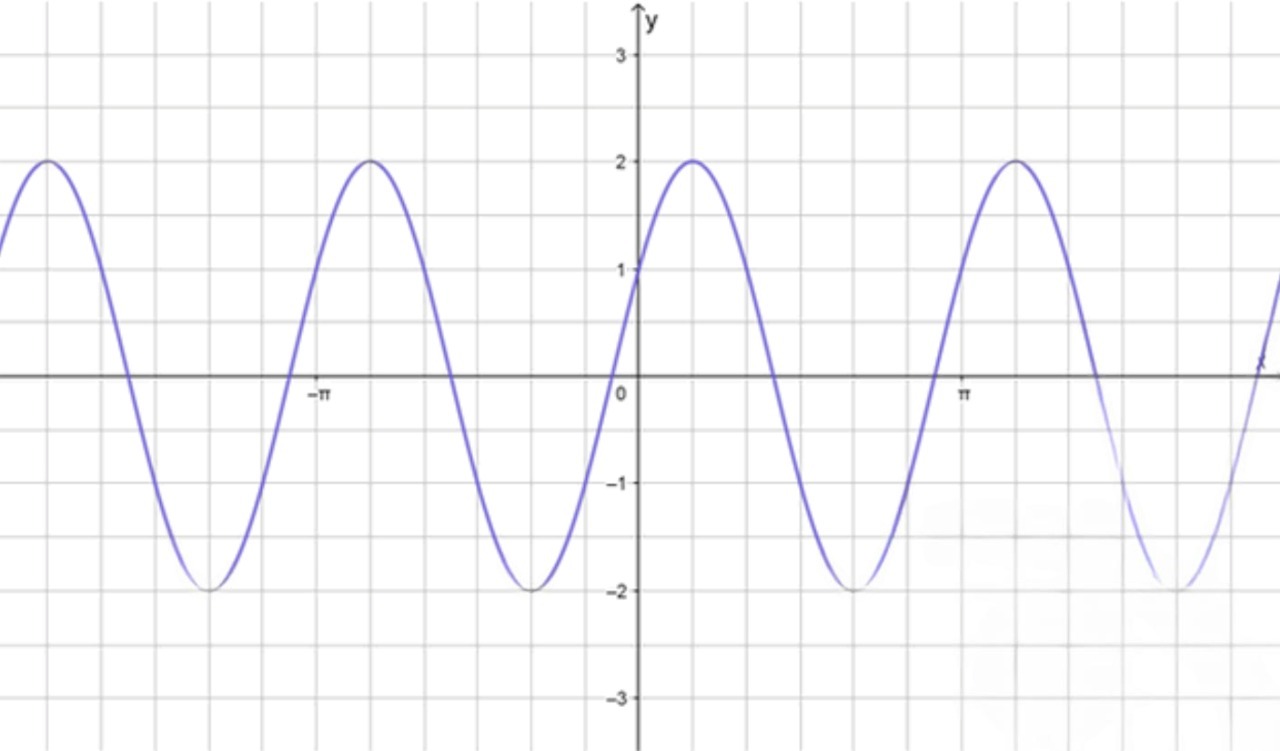
График функции:

б) $y = -2 \sin 3\left(x + \frac{\pi}{2}\right);$

Нули функции:

$$\sin 3\left(x + \frac{\pi}{2}\right) = 0;$$ $$3\left(x + \frac{\pi}{2}\right) = \pi n;$$ $$x + \frac{\pi}{2} = \frac{\pi n}{3};$$ $$x = -\frac{\pi}{2} + \frac{\pi n}{3};$$ $$x_0 = -\frac{\pi}{2} + \frac{\pi}{3} \cdot 0 = -\frac{\pi}{2};$$ $$x_1 = -\frac{\pi}{2} + \frac{\pi}{3} = -\frac{3\pi}{6} + \frac{2\pi}{6} = -\frac{\pi}{6};$$

Середина дуги:

$$x = \frac{1}{2}\left(-\frac{\pi}{2} — \frac{\pi}{6}\right) = \frac{1}{2} \cdot \left(-\frac{4\pi}{6}\right) = -\frac{4\pi}{12} = -\frac{\pi}{3};$$ $$y = -2 \sin 3\left(-\frac{\pi}{3} + \frac{\pi}{2}\right) = -2 \sin \frac{3\pi}{6} = -2 \sin \frac{\pi}{2} = -2;$$

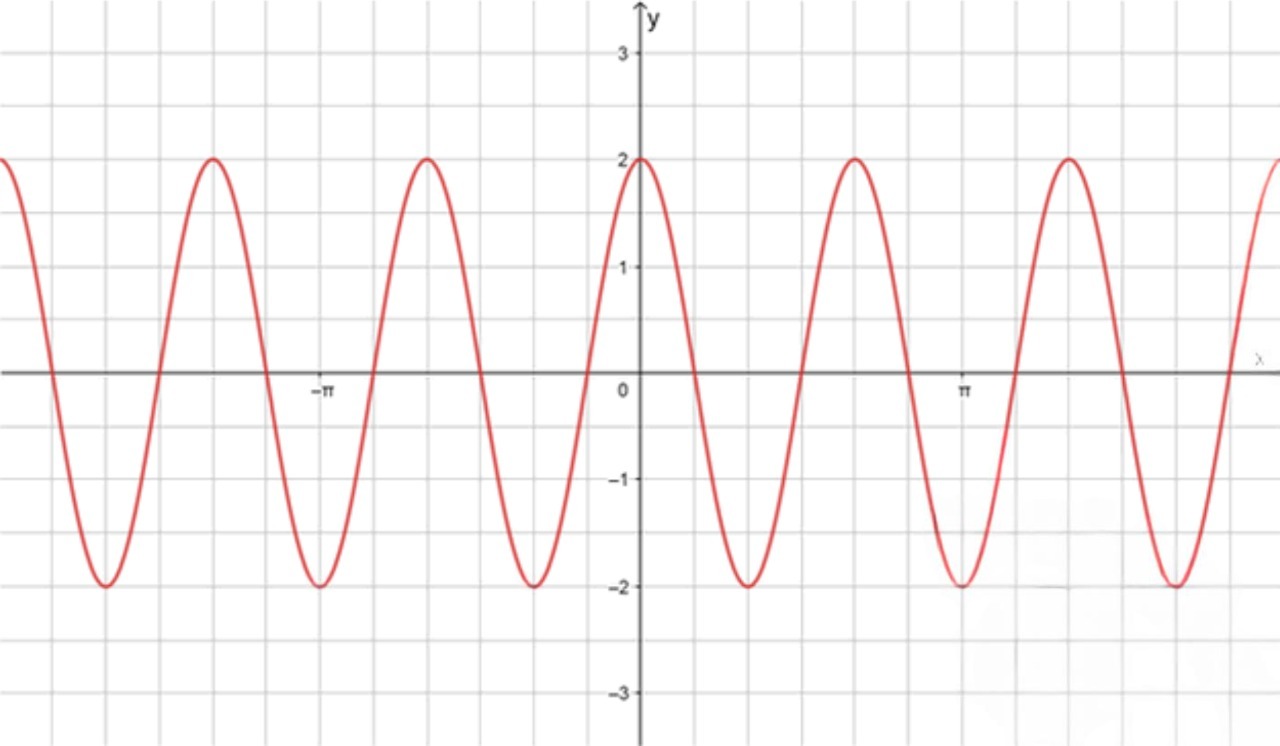
График функции:

Построить график функции:

а) $y = -2 \cos 2\left(x + \frac{\pi}{3}\right)$

Шаг 1. Анализ функции $y = -2 \cos 2\left(x + \frac{\pi}{3}\right)$

Это тригонометрическая функция косинуса, но с несколькими модификациями:

1. Амплитуда: коэффициент перед косинусом равен $-2$. Это означает, что график функции будет растянут по оси $y$ в 2 раза (амплитуда будет равна 2), но с отрицательным знаком, что приведет к инверсии графика. Вместо обычного косинуса, который начинается с максимума, график начнется с минимума.
2. Период: перед $x$ стоит коэффициент 2, который влияет на период функции. Период стандартной функции косинуса $\cos(x)$ равен $2\pi$, но умножение аргумента на 2 сокращает период в 2 раза. Таким образом, новый период функции:

   $$T = \frac{2\pi}{2} = \pi.$$

   Это означает, что график будет повторяться через каждые $\pi$ на оси $x$.

3. Сдвиг по оси $x$: выражение $\left( x + \frac{\pi}{3} \right)$ указывает на сдвиг графика функции косинуса на $-\frac{\pi}{3}$ по оси $x$. Это означает, что вся волна функции будет сдвинута влево на $\frac{\pi}{3}$.

Шаг 2. Нули функции

Нули функции $y = -2 \cos 2\left(x + \frac{\pi}{3}\right)$ соответствуют точкам, где косинус равен нулю.

Решим уравнение для косинуса:

$$\cos 2\left(x + \frac{\pi}{3}\right) = 0.$$

Косинус равен нулю в точках $2\left(x + \frac{\pi}{3}\right) = \pm \frac{\pi}{2} + 2\pi n$, где $n$ — целое число.

Умножаем на 2 обе стороны уравнения:

$$x + \frac{\pi}{3} = \pm \frac{\pi}{4} + \pi n.$$

Решим для $x$:

$$x = -\frac{\pi}{3} \pm \frac{\pi}{4} + \pi n.$$

Рассчитаем первые два нуля функции:

$$x_0 = -\frac{\pi}{3} — \frac{\pi}{4} = -\frac{4\pi}{12} — \frac{3\pi}{12} = -\frac{7\pi}{12},$$ $$x_1 = -\frac{\pi}{3} + \frac{\pi}{4} = -\frac{4\pi}{12} + \frac{3\pi}{12} = -\frac{\pi}{12}.$$

Таким образом, первые два нуля функции находятся в точках $x_0 = -\frac{7\pi}{12}$ и $x_1 = -\frac{\pi}{12}$.

Шаг 3. Середина дуги

Середина дуги — это точка, где функция достигает максимального значения на промежутке между двумя последовательными нулями. Рассмотрим промежуток между нулями $x_0 = -\frac{7\pi}{12}$ и $x_1 = -\frac{\pi}{12}$.

Абсцисса середины дуги:

$$x = \frac{1}{2} \left( -\frac{7\pi}{12} + \left(-\frac{\pi}{12}\right) \right) = \frac{1}{2} \cdot \left( -\frac{8\pi}{12} \right) = -\frac{4\pi}{12} = -\frac{\pi}{3}.$$

Ордината середины дуги: подставим $x = -\frac{\pi}{3}$ в уравнение функции:

$$y = -2 \cos 2\left(-\frac{\pi}{3} + \frac{\pi}{3}\right) = -2 \cos 0 = -2.$$

Таким образом, значение функции в середине дуги равно $y = -2$.

Шаг 4. Период функции

Как мы уже отметили, период функции равен $\pi$, так как коэффициент перед $x$ равен 2.

Шаг 5. График функции

График функции будет иметь следующие характеристики:

• Функция начнется с минимального значения $y = -2$ в точке $x = -\frac{7\pi}{12}$.
• В точке $x = -\frac{\pi}{12}$ функция снова пересечет ось $x$, но с другой фазой из-за сдвига.
• Период функции равен $\pi$, поэтому она будет повторяться через каждые $\pi$ единиц на оси $x$.

б) $y = -2 \sin 3\left(x + \frac{\pi}{2}\right)$

Шаг 1. Анализ функции $y = -2 \sin 3\left(x + \frac{\pi}{2}\right)$

Это тригонометрическая функция синуса с несколькими модификациями:

1. Амплитуда: коэффициент перед синусом равен $-2$, что означает, что график функции будет растянут по оси $y$ в 2 раза и инвертирован. Таким образом, график будет начинаться с минимального значения.
2. Период: перед $x$ стоит коэффициент 3, который влияет на период функции. Период стандартной функции синуса $\sin(x)$ равен $2\pi$, но умножение аргумента на 3 сокращает период в 3 раза. Таким образом, новый период функции:

   $$T = \frac{2\pi}{3}.$$

   Это означает, что график будет повторяться через каждые $\frac{2\pi}{3}$ на оси $x$.

3. Сдвиг по оси $x$: выражение $\left( x + \frac{\pi}{2} \right)$ указывает на сдвиг графика функции синуса на $-\frac{\pi}{2}$ по оси $x$. Это означает, что вся волна функции будет сдвинута влево на $\frac{\pi}{2}$.

Шаг 2. Нули функции

Нули функции $y = -2 \sin 3\left(x + \frac{\pi}{2}\right)$ соответствуют точкам, где синус равен нулю.

Решим уравнение для синуса:

$$\sin 3\left(x + \frac{\pi}{2}\right) = 0.$$

Синус равен нулю в точках $3\left(x + \frac{\pi}{2}\right) = \pi n$, где $n$ — целое число.

Умножаем обе стороны уравнения на 3:

$$x + \frac{\pi}{2} = \frac{\pi n}{3}.$$

Решим для $x$:

$$x = -\frac{\pi}{2} + \frac{\pi n}{3}.$$

Рассчитаем первые два нуля функции:

$$x_0 = -\frac{\pi}{2} + \frac{\pi}{3} \cdot 0 = -\frac{\pi}{2},$$ $$x_1 = -\frac{\pi}{2} + \frac{\pi}{3} = -\frac{3\pi}{6} + \frac{2\pi}{6} = -\frac{\pi}{6}.$$

Таким образом, первые два нуля функции находятся в точках $x_0 = -\frac{\pi}{2}$ и $x_1 = -\frac{\pi}{6}$.

Шаг 3. Середина дуги

Середина дуги — это точка, где функция достигает максимального значения на промежутке между двумя последовательными нулями. Рассмотрим промежуток между нулями $x_0 = -\frac{\pi}{2}$ и $x_1 = -\frac{\pi}{6}$.

Абсцисса середины дуги:

$$x = \frac{1}{2} \left( -\frac{\pi}{2} + \left(-\frac{\pi}{6}\right) \right) = \frac{1}{2} \cdot \left( -\frac{4\pi}{6} \right) = -\frac{4\pi}{12} = -\frac{\pi}{3}.$$

Ордината середины дуги: подставим $x = -\frac{\pi}{3}$ в уравнение функции:

$$y = -2 \sin 3\left(-\frac{\pi}{3} + \frac{\pi}{2}\right) = -2 \sin \frac{3\pi}{6} = -2 \sin \frac{\pi}{2} = -2.$$

Таким образом, значение функции в середине дуги равно $y = -2$.

Шаг 4. Период функции

Как мы уже отметили, период функции равен $\frac{2\pi}{3}$, так как коэффициент перед $x$ равен 3.

Шаг 5. График функции

График функции будет иметь следующие характеристики:

• Функция начнется с минимального значения $y = -2$ в точке $x = -\frac{\pi}{2}$.
• В точке $x = -\frac{\pi}{6}$ функция снова пересечет ось $x$, но с другой фазой из-за сдвига.
• Период функции равен $\frac{2\pi}{3}$, поэтому она будет повторяться через каждые $\frac{2\pi}{3}$ единиц на оси $x$.