ГДЗ 10-11 Класс Номер 13.7 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = 2 \sin x — 1$;

б) $y = -\frac{1}{2} \cos x + 2$;

в) $y = -\frac{3}{2} \sin x + 3$;

г) $y = 3 \cos x — 2$

Построить график функции:

а) $y = 2 \sin x — 1$;

Построим дугу графика $y = \sin x$:

• Растянем ее в 2 раза от оси абсцисс;
• Переместим ее на 1 единицу вниз;

Достроим график функции:

б) $y = -\frac{1}{2} \cos x + 2$;

Построим дугу графика $y = \cos x$:

• Отразим ее относительно оси абсцисс;
• Сожмем ее в 2 раза к оси абсцисс;
• Переместим ее на 2 единицы вверх;

Достроим график функции:

в) $y = -\frac{3}{2} \sin x + 3$;

Построим дугу графика $y = \sin x$:

• Отразим ее относительно оси абсцисс;
• Растянем ее в 1,5 раза от оси абсцисс;
• Переместим ее на 3 единицы вверх;

Достроим график функции:

г) $y = 3 \cos x — 2$;

Построим дугу графика $y = \cos x$:

• Растянем ее в 3 раза от оси абсцисс;
• Переместим ее на 2 единицы вниз;

Достроим график функции:

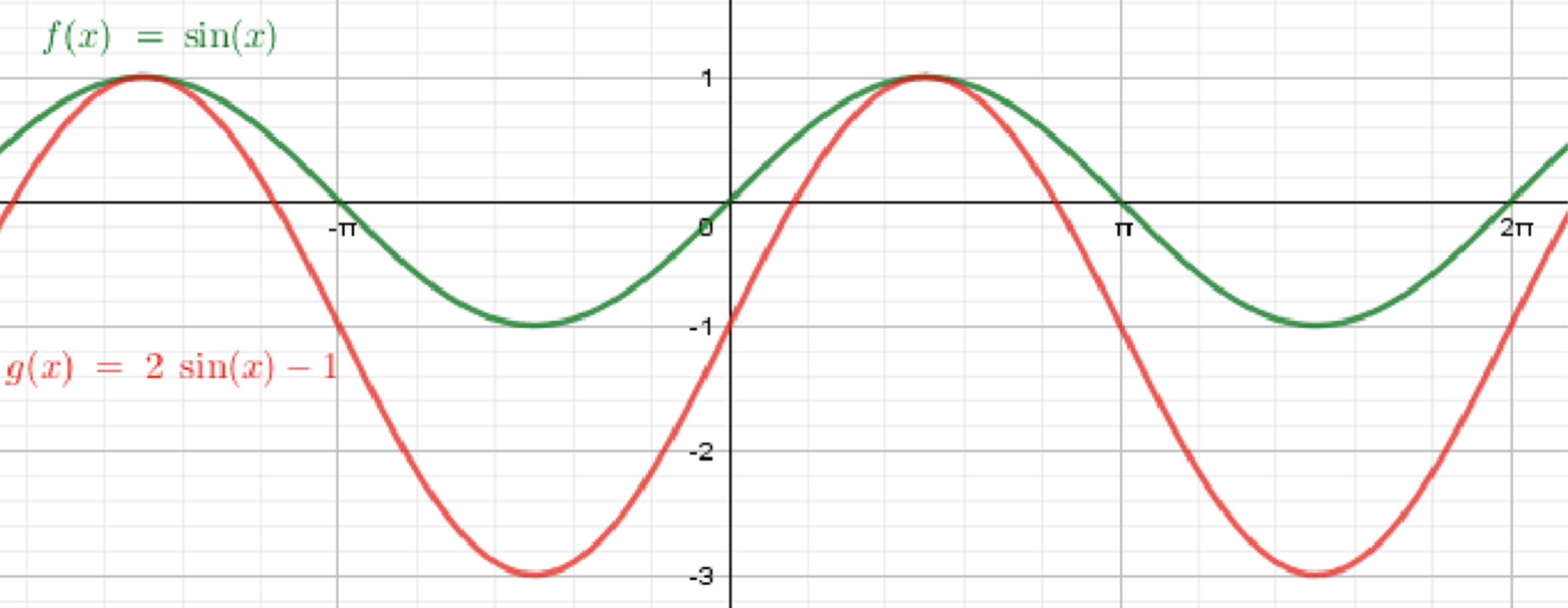
а) $y = 2 \sin x — 1$

1. Исходная функция:
   Начнем с графика функции $y = \sin x$. Это стандартная синусоида, которая колеблется между значениями $-1$ и $1$, с периодом $2\pi$.
2. Первое преобразование — растяжение на коэффициент 2 вдоль оси $y$:
   При изменении функции с $y = \sin x$ на $y = 2 \sin x$, амплитуда функции увеличивается в 2 раза. Это означает, что график функции будет колебаться между значениями $-2$ и $2$, а период останется $2\pi$.
3. Второе преобразование — сдвиг вниз на 1 единицу:
   При добавлении $-1$ ко всей функции происходит вертикальный сдвиг графика вниз на 1 единицу. Таким образом, новые максимумы и минимумы функции будут находиться на уровнях $1$ и $-3$ соответственно, а период снова останется $2\pi$.

Ответ: Получаем график функции $y = 2 \sin x — 1$, где амплитуда увеличена в 2 раза, а график сдвинут на 1 единицу вниз.

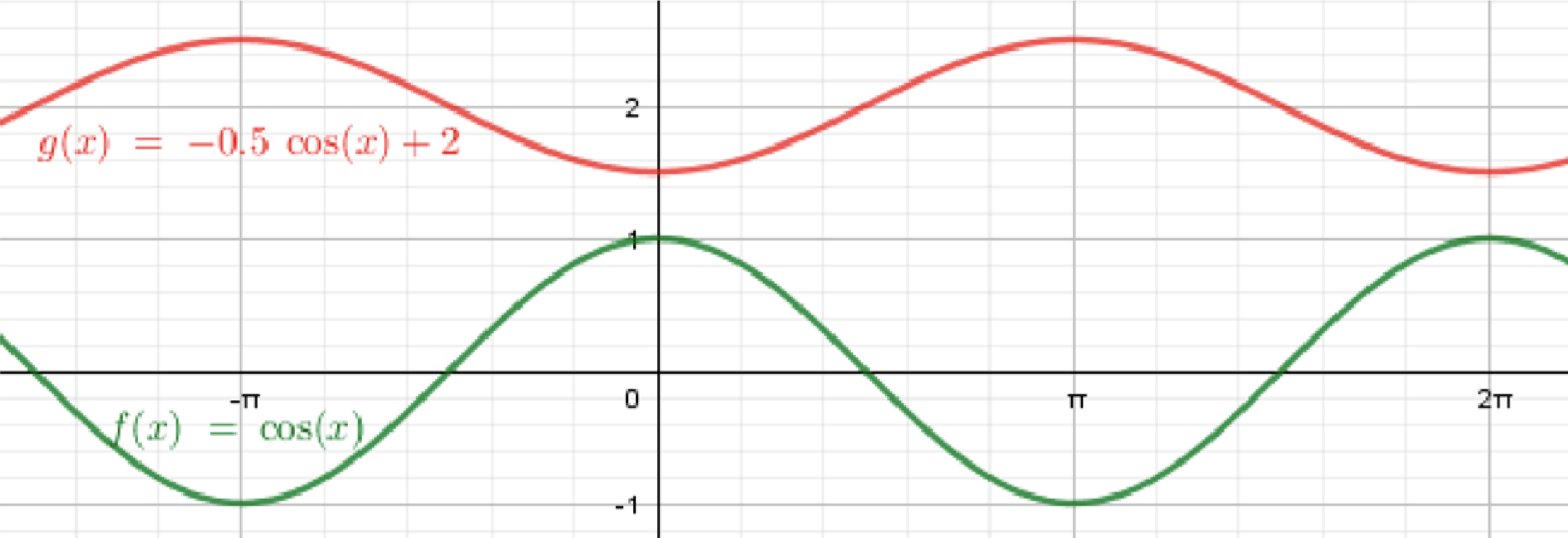
б) $y = -\frac{1}{2} \cos x + 2$

1. Исходная функция:
   Начнем с графика функции $y = \cos x$. Это стандартная косинусоида, которая колеблется между значениями $-1$ и $1$, с периодом $2\pi$.
2. Первое преобразование — отражение относительно оси $x$:
   При изменении функции с $y = \cos x$ на $y = -\cos x$ происходит отражение графика функции относительно оси $x$. Это значит, что теперь максимум функции будет на уровне $-1$, а минимум на уровне $1$, а период останется $2\pi$.
3. Второе преобразование — сжатие вдоль оси $y$ на коэффициент $\frac{1}{2}$:
   При умножении функции на $-\frac{1}{2}$ происходит сжатие графика вдоль оси $y$ в 2 раза. Это означает, что график теперь будет колебаться между значениями $-\frac{1}{2}$ и $\frac{1}{2}$, а период по-прежнему будет равен $2\pi$.
4. Третье преобразование — сдвиг вверх на 2 единицы:
   При добавлении $+2$ ко всей функции происходит вертикальный сдвиг графика вверх на 2 единицы. Таким образом, новые максимумы и минимумы функции будут находиться на уровнях $2.5$ и $1.5$ соответственно, а период, как и раньше, останется $2\pi$.

Ответ: Получаем график функции $y = -\frac{1}{2} \cos x + 2$, где график отражен относительно оси $x$, сжат вдоль оси $y$ и сдвинут вверх на 2 единицы.

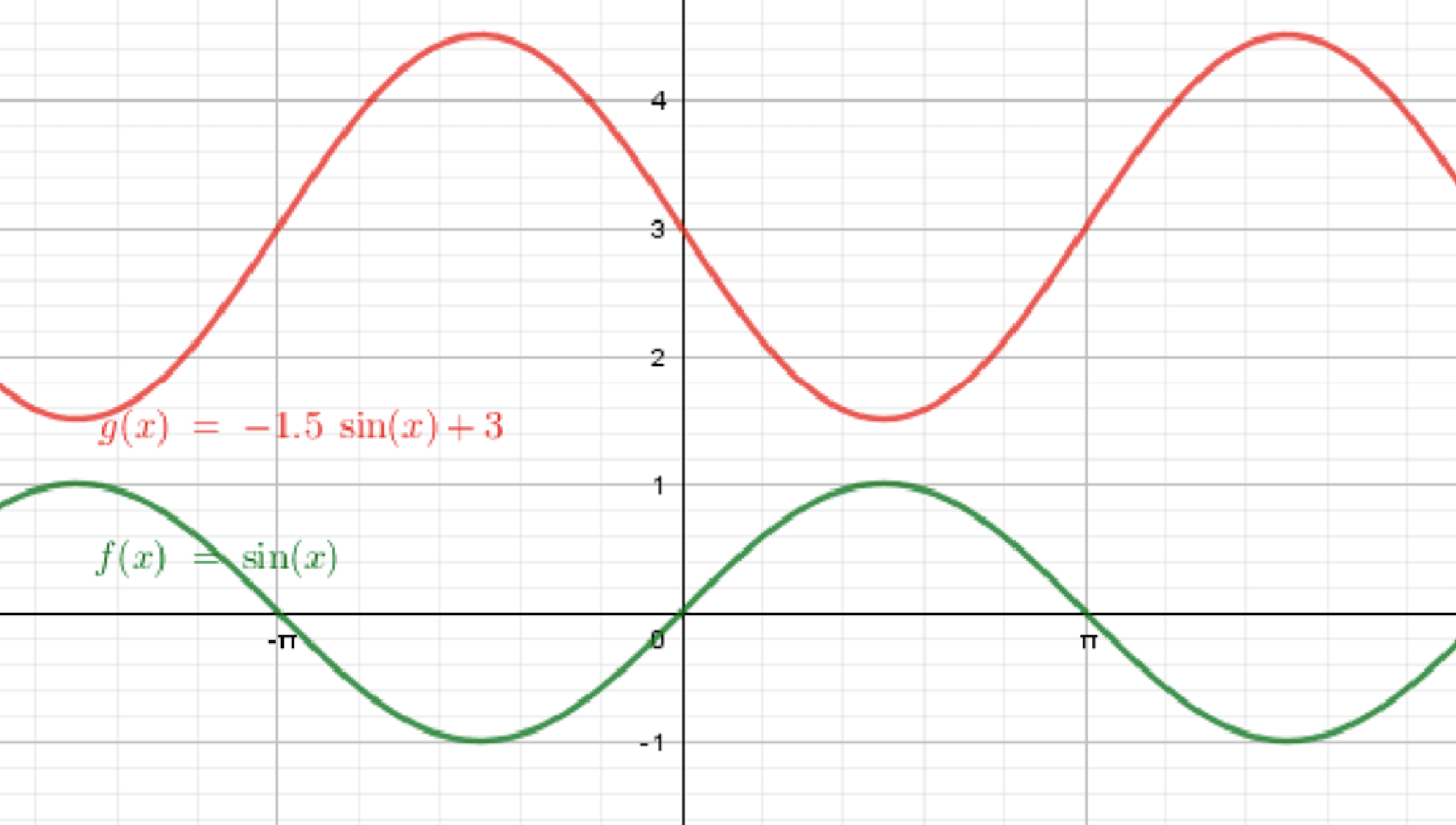
в) $y = -\frac{3}{2} \sin x + 3$

1. Исходная функция:
   Начнем с графика функции $y = \sin x$. Это стандартная синусоида, которая колеблется между значениями $-1$ и $1$, с периодом $2\pi$.
2. Первое преобразование — отражение относительно оси $x$:
   При изменении функции с $y = \sin x$ на $y = -\sin x$ происходит отражение графика функции относительно оси $x$. Это означает, что максимум функции теперь будет на уровне $-1$, а минимум на уровне $1$, а период останется $2\pi$.
3. Второе преобразование — растяжение вдоль оси $y$ на коэффициент $\frac{3}{2}$:
   При умножении функции на $-\frac{3}{2}$ происходит растяжение графика вдоль оси $y$ в 1.5 раза. Это означает, что график теперь будет колебаться между значениями $-\frac{3}{2}$ и $\frac{3}{2}$, а период останется $2\pi$.
4. Третье преобразование — сдвиг вверх на 3 единицы:
   При добавлении $+3$ ко всей функции происходит вертикальный сдвиг графика вверх на 3 единицы. Таким образом, новые максимумы и минимумы функции будут находиться на уровнях $4.5$ и $1.5$ соответственно, а период, как и раньше, останется $2\pi$.

Ответ: Получаем график функции $y = -\frac{3}{2} \sin x + 3$, где график отражен относительно оси $x$, растянут вдоль оси $y$ и сдвинут вверх на 3 единицы.

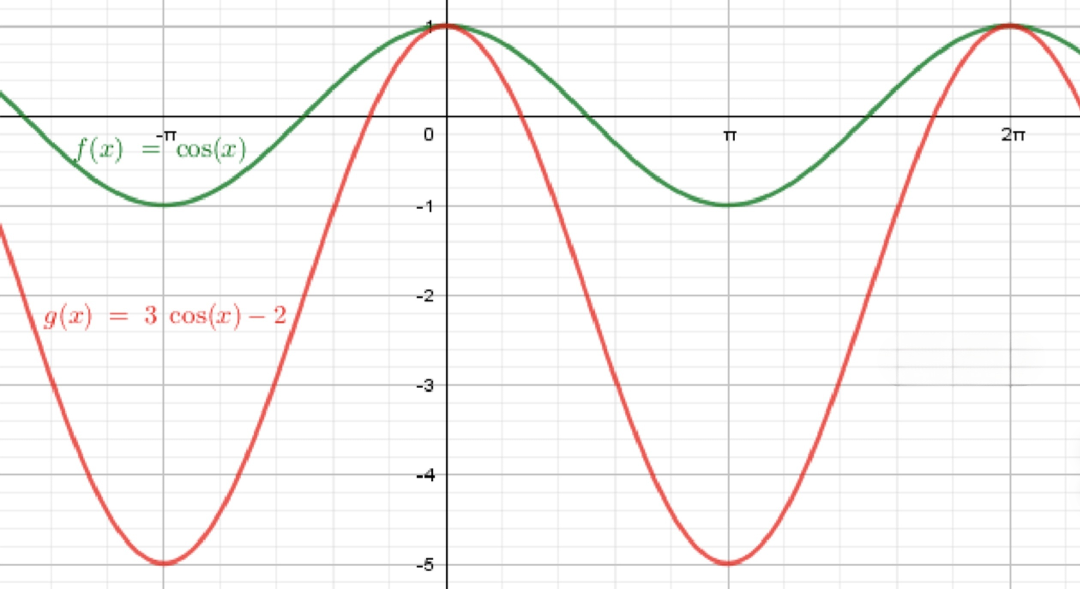
г) $y = 3 \cos x — 2$

1. Исходная функция:
   Начнем с графика функции $y = \cos x$. Это стандартная косинусоида, которая колеблется между значениями $-1$ и $1$, с периодом $2\pi$.
2. Первое преобразование — растяжение вдоль оси $y$ на коэффициент 3:
   При изменении функции с $y = \cos x$ на $y = 3 \cos x$ происходит растяжение графика вдоль оси $y$ в 3 раза. Это означает, что график теперь будет колебаться между значениями $-3$ и $3$, а период останется $2\pi$.
3. Второе преобразование — сдвиг вниз на 2 единицы:
   При добавлении $-2$ ко всей функции происходит вертикальный сдвиг графика вниз на 2 единицы. Таким образом, новые максимумы и минимумы функции будут находиться на уровнях $1$ и $-5$ соответственно, а период по-прежнему останется $2\pi$.

Ответ: Получаем график функции $y = 3 \cos x — 2$, где график растянут вдоль оси $y$ и сдвинут вниз на 2 единицы.