ГДЗ 10-11 Класс Номер 14.17 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \operatorname{tg}\left(x + \frac{\pi}{2}\right);$

б) $y = \operatorname{tg} x + 1;$

в) $y = \operatorname{tg}\left(x — \frac{\pi}{4}\right);$

г) $y=\mathrm{tg}x-2$$$

Построить график функции:

а) $y = \operatorname{tg}\left(x + \frac{\pi}{2}\right);$

Главная ветвь имеет центр в точке:
$x_0 = -\frac{\pi}{2}, \, y_0 = 0;$

Ветвь лежит на интервале:
$-\frac{\pi}{2} — \frac{\pi}{2} < x < \frac{\pi}{2} — \frac{\pi}{2};$
$-\pi < x < 0;$

График функции:

б) $y = \operatorname{tg} x + 1;$

Главная ветвь имеет центр в точке:
$x_0 = 0, \, y_0 = 1;$

Ветвь лежит на интервале:
$-\frac{\pi}{2} < x < \frac{\pi}{2};$

График функции:

в) $y = \operatorname{tg}\left(x — \frac{\pi}{4}\right);$

Главная ветвь имеет центр в точке:
$x_0 = \frac{\pi}{4}, \, y_0 = 0;$

Ветвь лежит на интервале:
$-\frac{\pi}{2} + \frac{\pi}{4} < x < \frac{\pi}{2} + \frac{\pi}{4};$
$-\frac{\pi}{4} < x < \frac{3\pi}{4};$

График функции:

г) $y = \operatorname{tg} x — 2;$

Главная ветвь имеет центр в точке:
$x_0 = 0, \, y_0 = -2;$

Ветвь лежит на интервале:
$-\frac{\pi}{2} < x < \frac{\pi}{2};$

График функции:

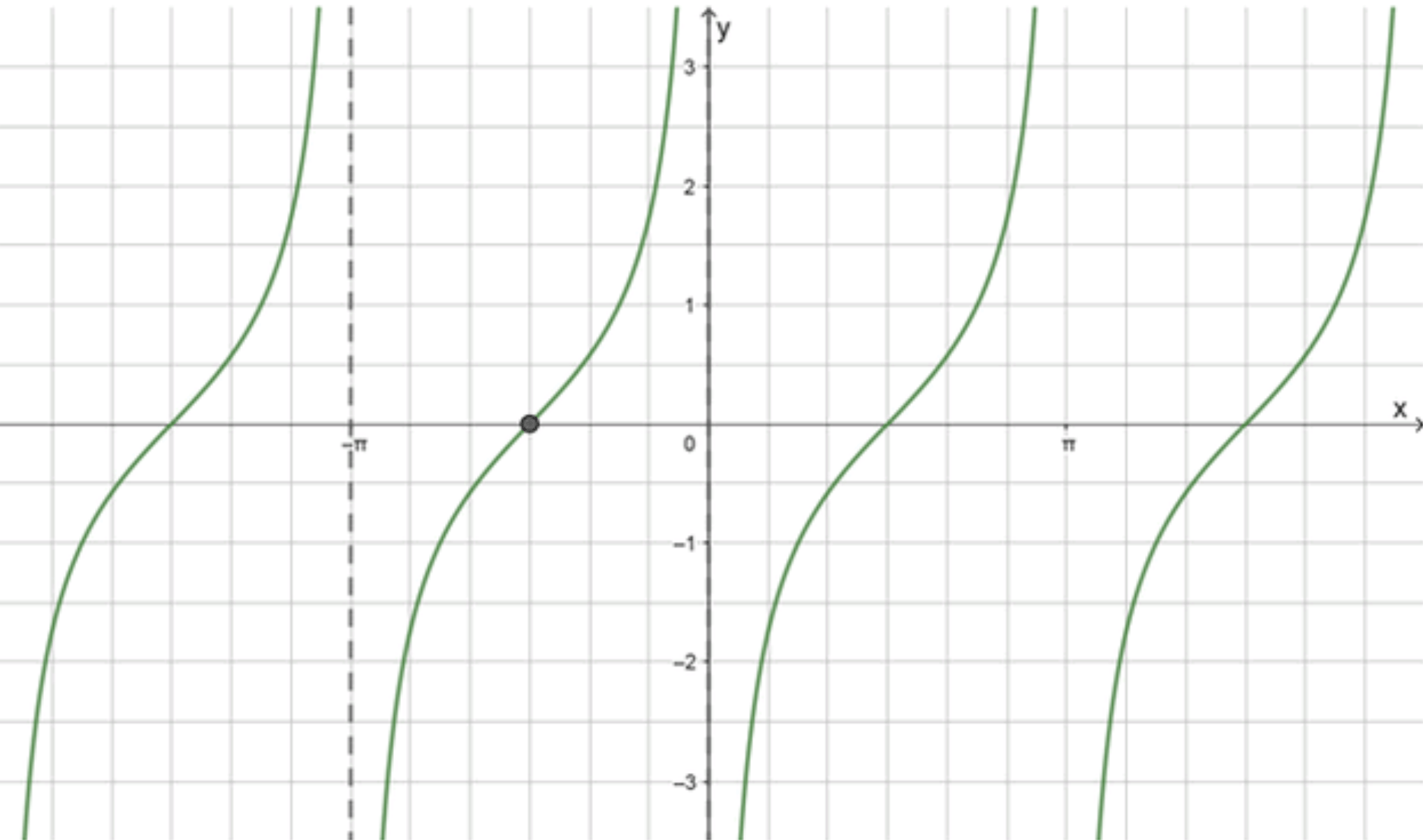
а) $y = \operatorname{tg}\left(x + \frac{\pi}{2}\right)$

Шаг 1: Анализ функции

Функция $y = \operatorname{tg}(x + \frac{\pi}{2})$ является трансформацией стандартной функции тангенса. Здесь происходит сдвиг на $\frac{\pi}{2}$ вправо.

Основные особенности тангенса:

• $\operatorname{tg} x$ имеет вертикальные асимптоты в точках $x = \frac{\pi}{2} + n\pi$, где $n$ — целое число.
• Функция имеет период $\pi$, то есть, повторяется через $\pi$.

Шаг 2: Найдем центр графика

Когда функция имеет вид $y = \operatorname{tg}(x + \frac{\pi}{2})$, то происходит сдвиг на $\frac{\pi}{2}$ вправо. Это означает, что центр графика тангенса, который обычно находится в точке $x_0 = 0$, теперь будет в точке $x_0 = -\frac{\pi}{2}$.

• Таким образом, центр графика находится в точке $(x_0, y_0) = (-\frac{\pi}{2}, 0)$.

Шаг 3: Интервал, на котором определена функция

Тангенс имеет вертикальные асимптоты в точках вида $x = \frac{\pi}{2} + n\pi$. Для функции $y = \operatorname{tg}(x + \frac{\pi}{2})$, асимптоты будут происходить в точках, получаемых из $x + \frac{\pi}{2} = \frac{\pi}{2} + n\pi$, что приводит к асимптотам на интервале $-\pi < x < 0$. Этот интервал ограничивает область, в которой функция определена.

Шаг 4: Построение графика

• График функции будет иметь вертикальную асимптоту в точке $x = -\pi$ и $x = 0$.
• Ветвь будет пересекать ось $y = 0$ в точке $x = -\frac{\pi}{2}$.
• График будет идти от отрицательных значений к положительным, между асимптотами.

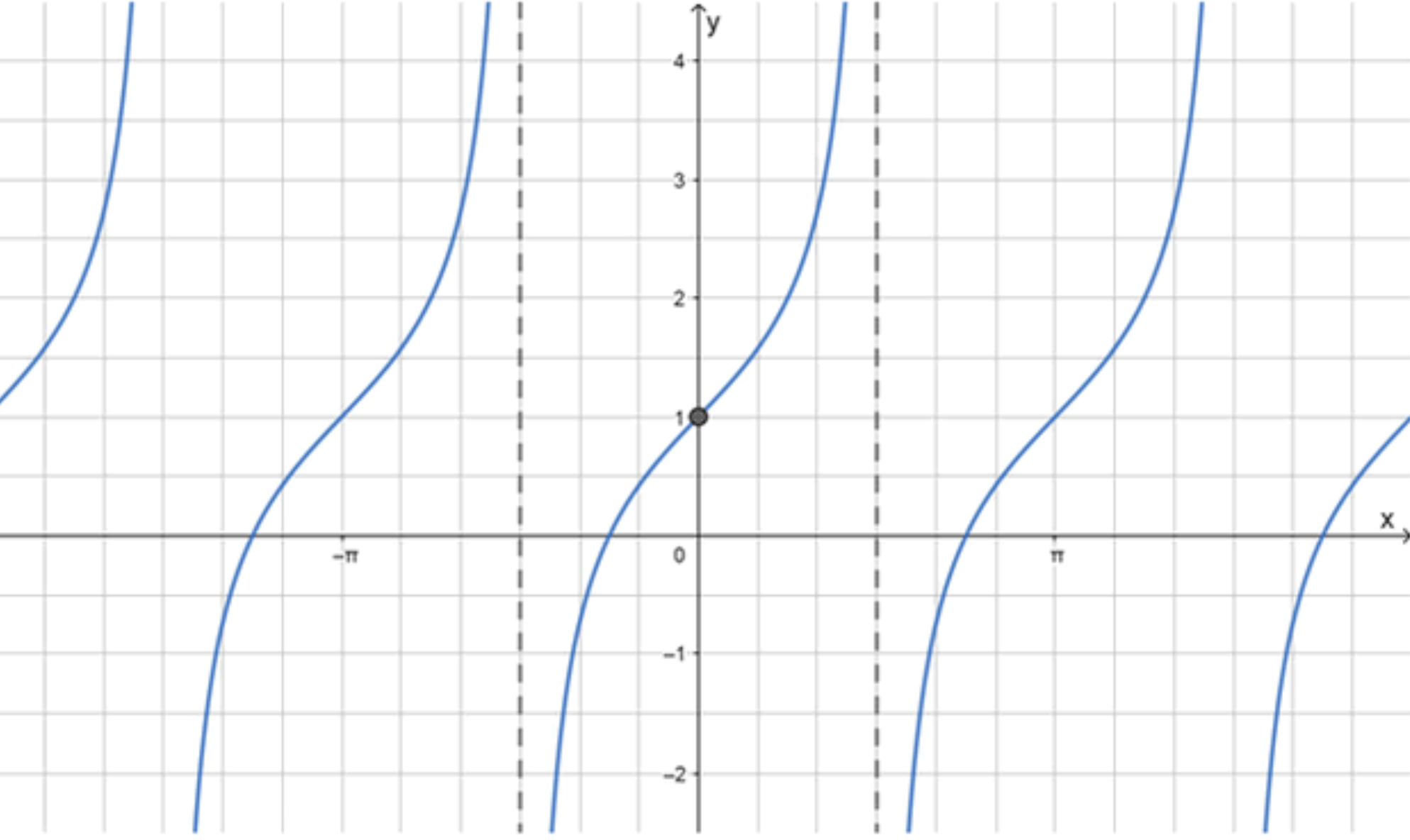
б) $y = \operatorname{tg} x + 1$

Шаг 1: Анализ функции

Функция $y = \operatorname{tg} x + 1$ является результатом сдвига стандартного графика тангенса на 1 единицу вверх.

• В данном случае период функции не изменяется, и вертикальные асимптоты остаются на тех же местах, что и у стандартной функции тангенса — $x = \frac{\pi}{2} + n\pi$.
• Центр графика сдвигается на 1 единицу вверх, что означает, что точка $(x_0, y_0)$ будет $(0, 1)$.

Шаг 2: Найдем центр графика

Центр графика будет в точке $(0, 1)$, так как мы сдвинули стандартный график на 1 единицу вверх.

Шаг 3: Интервал, на котором определена функция

Тангенс имеет вертикальные асимптоты в точках $x = \frac{\pi}{2} + n\pi$, так что функция определена на интервале $-\frac{\pi}{2} < x < \frac{\pi}{2}$.

Шаг 4: Построение графика

• График будет пересекать ось $y = 1$ в точке $x = 0$.
• Ветви будут направлены от $-\infty$ к $+\infty$, но будут сдвинуты на 1 единицу вверх.
• Асимптоты остаются на местах $x = -\frac{\pi}{2}$ и $x = \frac{\pi}{2}$.

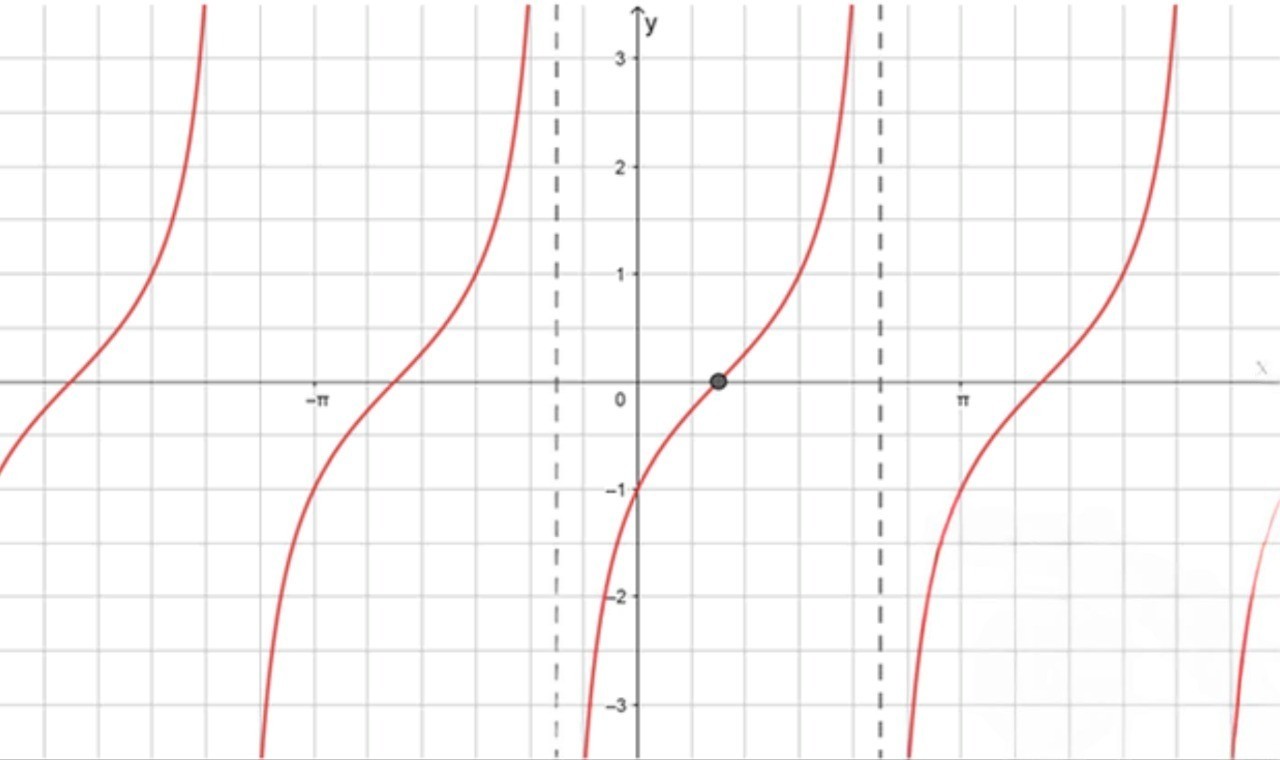
в) $y = \operatorname{tg}\left(x — \frac{\pi}{4}\right)$

Шаг 1: Анализ функции

Функция $y = \operatorname{tg}\left(x — \frac{\pi}{4}\right)$ является результатом сдвига графика тангенса на $\frac{\pi}{4}$ вправо.

• Сдвиг вправо на $\frac{\pi}{4}$ изменяет положение вертикальных асимптот. Если стандартный график тангенса имеет асимптоты в точках $x = \frac{\pi}{2} + n\pi$, то для функции $y = \operatorname{tg}\left(x — \frac{\pi}{4}\right)$ асимптоты будут сдвинуты на $\frac{\pi}{4}$ вправо, то есть в точки $x = \frac{\pi}{4}, \frac{5\pi}{4}$ и так далее.

Шаг 2: Найдем центр графика

Центр графика будет в точке $x_0 = \frac{\pi}{4}$, и $y_0 = 0$. Это связано с тем, что $\operatorname{tg}(x — \frac{\pi}{4})$ имеет ноль в точке $x = \frac{\pi}{4}$.

Шаг 3: Интервал, на котором определена функция

Асимптоты находятся в точках $x = -\frac{\pi}{4}$ и $x = \frac{3\pi}{4}$, что даёт интервал $-\frac{\pi}{4} < x < \frac{3\pi}{4}$.

Шаг 4: Построение графика

• График будет пересекать ось $y = 0$ в точке $x = \frac{\pi}{4}$.
• Асимптоты будут находиться в точках $x = -\frac{\pi}{4}$ и $x = \frac{3\pi}{4}$.
• Ветви будут располагаться между асимптотами, а функция будет стремиться к бесконечности, приближаясь к асимптотам.

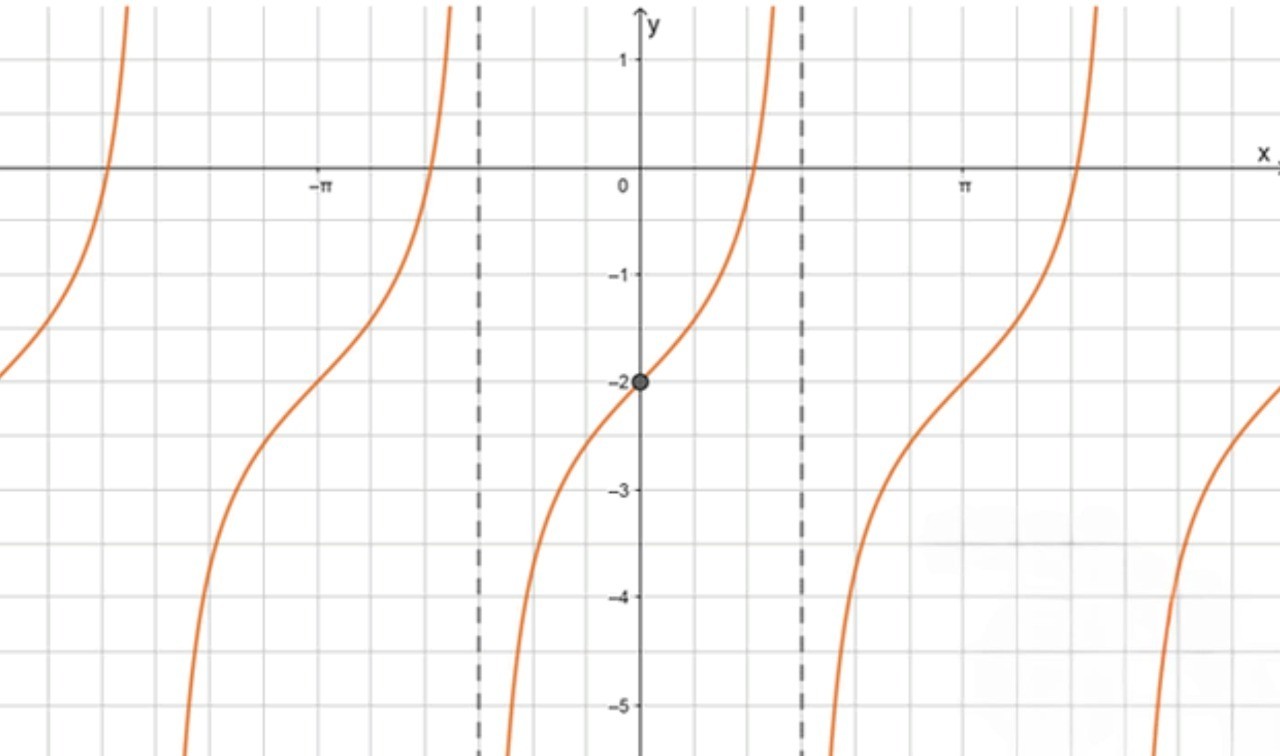
г) $y = \operatorname{tg} x — 2$

Шаг 1: Анализ функции

Функция $y = \operatorname{tg} x — 2$ является результатом сдвига графика тангенса на 2 единицы вниз.

• Период и асимптоты остаются неизменными. Функция имеет вертикальные асимптоты в точках $x = \frac{\pi}{2} + n\pi$, а центр графика сдвинут вниз.

Шаг 2: Найдем центр графика

Центр графика будет в точке $(0, -2)$, так как весь график сдвинут вниз на 2 единицы.

Шаг 3: Интервал, на котором определена функция

Как и в предыдущих примерах, асимптоты будут находиться на интервале $-\frac{\pi}{2} < x < \frac{\pi}{2}$.

Шаг 4: Построение графика

• График будет пересекать ось $y = -2$ в точке $x = 0$.
• Асимптоты будут находиться на интервале $-\frac{\pi}{2}$ и $\frac{\pi}{2}$.
• Ветви будут идти от минус бесконечности до плюс бесконечности, но будут сдвинуты на 2 единицы вниз.