ГДЗ 10-11 Класс Номер 14.21 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y=2\cdot \mathrm{tg}x\cdot \mathrm{ctg}x$

б) $y=\mathrm{tg}x\cdot \mathrm{ctg}x+\sqrt{x}$

Построить график функции:

а) $y = 2 \cdot \operatorname{tg} x \cdot \operatorname{ctg} x = 2 \cdot 1 = 2$;

Область определения:

$$x_1 \neq \frac{\pi}{2} + \pi n;$$ $$x_2 \neq \pi n;$$

График функции:

б) $y = \operatorname{tg} x \cdot \operatorname{ctg} x + \sqrt{x} = 1 + \sqrt{x}$;

Область определения:

$$x_1 \neq \frac{\pi}{2} + \pi n;$$ $$x_2 \neq \pi n;$$ $$x \geq 0;$$

График функции:

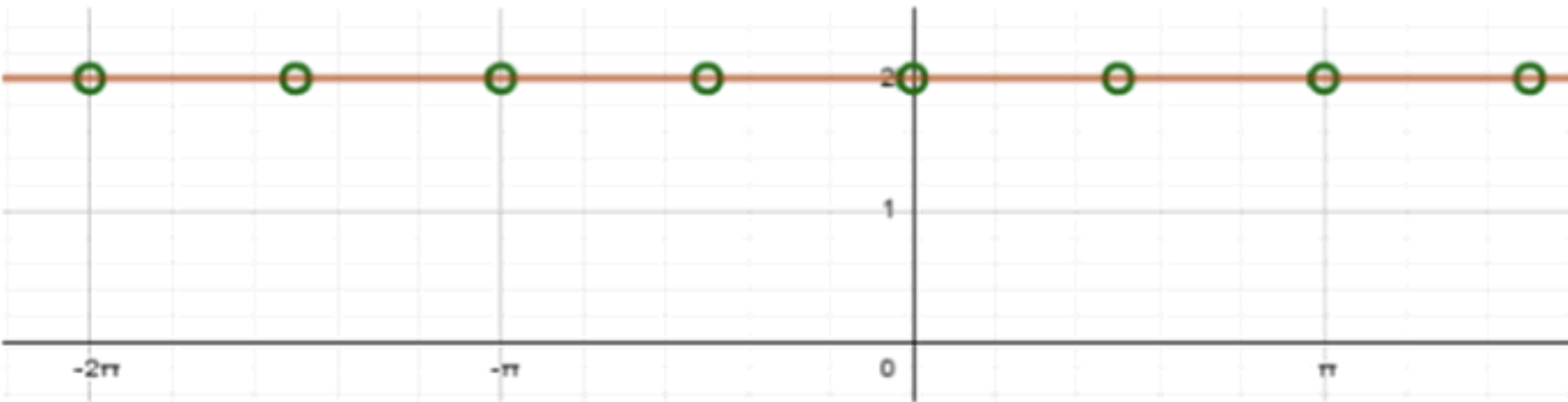
а) $y = 2 \cdot \operatorname{tg} x \cdot \operatorname{ctg} x = 2 \cdot 1 = 2$

Шаг 1: Анализ функции

Данная функция является произведением тангенса и котангенса:

$$y = 2 \cdot \operatorname{tg} x \cdot \operatorname{ctg} x$$

Теперь, вспомним, что:

$$\operatorname{tg} x = \frac{\sin x}{\cos x}, \quad \operatorname{ctg} x = \frac{\cos x}{\sin x}$$

Если подставить это в выражение для функции $y$, то получим:

$$y = 2 \cdot \left( \frac{\sin x}{\cos x} \right) \cdot \left( \frac{\cos x}{\sin x} \right)$$

Упростим выражение:

$$y = 2 \cdot \frac{\sin x}{\cos x} \cdot \frac{\cos x}{\sin x} = 2 \cdot 1 = 2$$

Таким образом, функция $y = 2 \cdot \operatorname{tg} x \cdot \operatorname{ctg} x$ упрощается до константы $y = 2$, которая является горизонтальной прямой.

Шаг 2: Область определения

Так как в исходной функции были использованы тангенс и котангенс, необходимо определить, при каких значениях $x$ они определены:

• $\operatorname{tg} x$ и $\operatorname{ctg} x$ не определены в точках, где синус или косинус равен нулю. Это происходит в точках:
  • $x_1 \neq \frac{\pi}{2} + \pi n$, где $n$ — целое число (точки, где $\cos x = 0$ для $\operatorname{tg} x$).
  • $x_2 \neq \pi n$, где $n$ — целое число (точки, где $\sin x = 0$ для $\operatorname{ctg} x$).

Шаг 3: Построение графика

• График функции $y = 2$ — это просто горизонтальная прямая, проходящая через $y = 2$.
• Важные моменты: несмотря на то, что функция представляет собой постоянную, область определения не включает точки, где $\sin x = 0$ или $\cos x = 0$. Это означает, что график не будет существовать в точках $x = \frac{\pi}{2} + n\pi$ и $x = \pi n$, где $n$ — целое число.

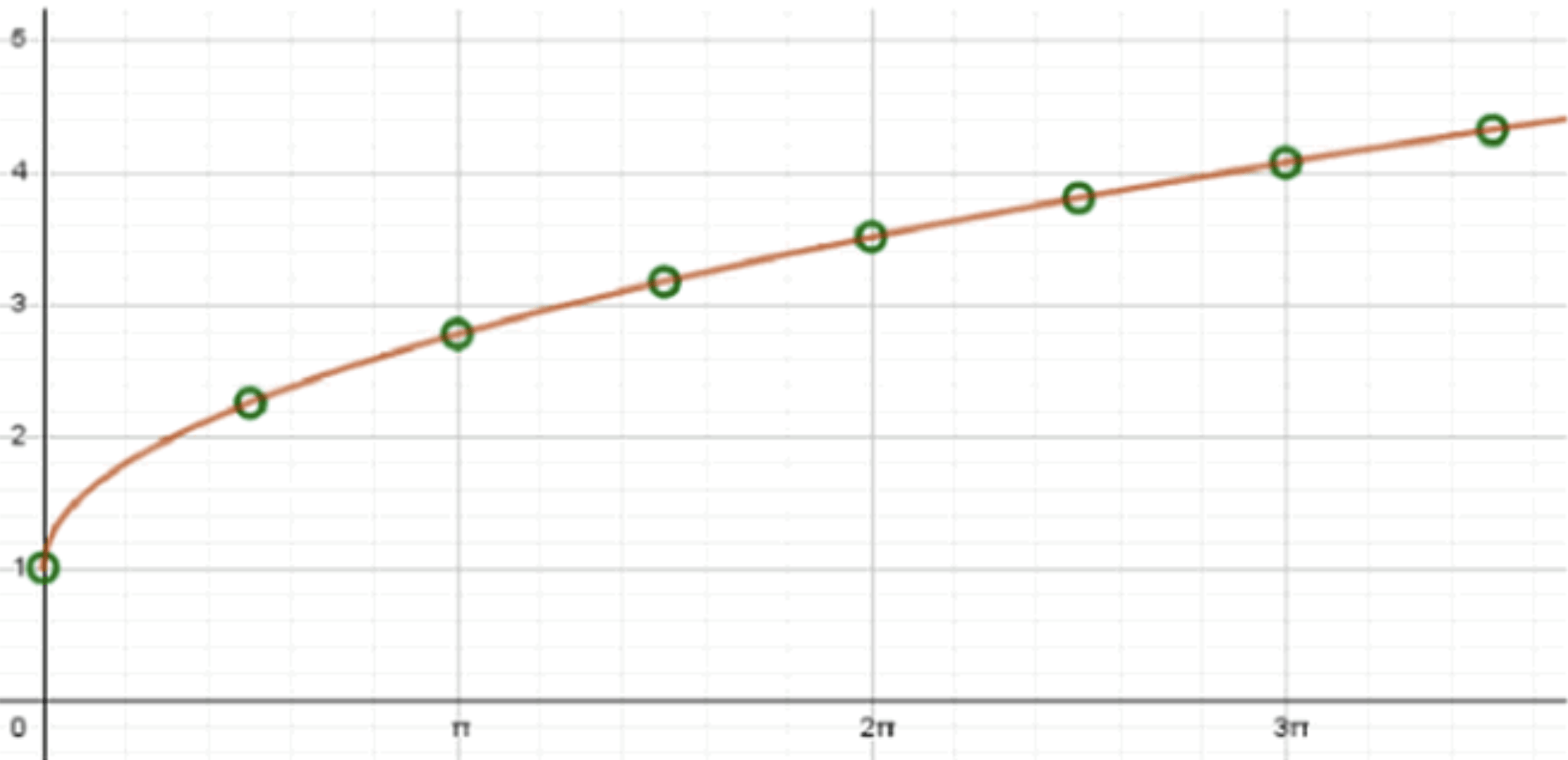
б) $y = \operatorname{tg} x \cdot \operatorname{ctg} x + \sqrt{x} = 1 + \sqrt{x}$

Шаг 1: Анализ функции

Здесь функция состоит из двух частей:

$$y = \operatorname{tg} x \cdot \operatorname{ctg} x + \sqrt{x}$$

Опять же, начнем с упрощения произведения $\operatorname{tg} x$ и $\operatorname{ctg} x$:

$$\operatorname{tg} x \cdot \operatorname{ctg} x = \frac{\sin x}{\cos x} \cdot \frac{\cos x}{\sin x} = 1$$

Таким образом, выражение для функции упрощается до:

$$y = 1 + \sqrt{x}$$

Это простая функция, которая складывает 1 с квадратным корнем из $x$.

Шаг 2: Область определения

Для того чтобы функция $y = 1 + \sqrt{x}$ была определена, $x$ должно быть неотрицательным (так как извлечение квадратного корня из отрицательных чисел в рамках действительных чисел не имеет смысла). Следовательно:

$$x \geq 0$$

Кроме того, мы должны учесть, что $\operatorname{tg} x \cdot \operatorname{ctg} x$ определено в тех же точках, что и в предыдущем случае:

• $\operatorname{tg} x$ не определен в точках $x_1 = \frac{\pi}{2} + \pi n$, где $n$ — целое число (где $\cos x = 0$).
• $\operatorname{ctg} x$ не определен в точках $x_2 = \pi n$, где $n$ — целое число (где $\sin x = 0$).

Таким образом, область определения функции:

$$x_1 \neq \frac{\pi}{2} + \pi n$$ $$x_2 \neq \pi n$$ $$x \geq 0$$

Шаг 3: Построение графика

• График функции $y = 1 + \sqrt{x}$ — это стандартный график функции квадратного корня, сдвинутый вверх на 1 единицу.
• Однако важно помнить, что график не будет существовать для значений $x$, равных $\pi n$ или $\frac{\pi}{2} + \pi n$, так как в этих точках котангенс и тангенс не определены.