ГДЗ 10-11 Класс Номер 14.22 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y={\sin }^2(\mathrm{tg}x)+{\cos }^2(\mathrm{tg}x)\mathrm{}$

б) $y=2{\cos }^2(\mathrm{ctg}x)+2{\sin }^2(\mathrm{ctg}x)\mathrm{}$

Построить график функции:

а) $y = \sin^2(\operatorname{tg} x) + \cos^2(\operatorname{tg} x) = 1$;

Область определения:
$x \neq \frac{\pi}{2} + \pi n;$

График функции:

б) $y = 2\cos^2(\operatorname{ctg} x) + 2\sin^2(\operatorname{ctg} x) = 2$;

Область определения:
$x \neq \pi n;$

График функции:

а) $y = \sin^2(\operatorname{tg} x) + \cos^2(\operatorname{tg} x) = 1$

Шаг 1: Анализ функции

В данном случае функция имеет вид:

$$y = \sin^2(\operatorname{tg} x) + \cos^2(\operatorname{tg} x)$$

Это выражение напоминает основной тригонометрический тождество, которое говорит, что:

$$\sin^2 \theta + \cos^2 \theta = 1$$

Здесь мы заменяем $\theta$ на $\operatorname{tg} x$, что не изменяет самого тождества:

$$y = 1$$

Таким образом, функция упрощается до постоянной функции $y = 1$.

Шаг 2: Область определения

Для того чтобы функция была определена, необходимо, чтобы $\operatorname{tg} x$ существовал. Это требует, чтобы $x$ не принимал значения, при которых $\operatorname{tg} x$ не существует. Тангенс не существует в точках, где $\cos x = 0$, то есть:

$$x \neq \frac{\pi}{2} + \pi n$$

где $n$ — целое число. Эти точки — вертикальные асимптоты функции тангенса, и они также являются точками, в которых исходная функция не определена.

Шаг 3: Построение графика

• График функции $y = 1$ представляет собой горизонтальную прямую, которая пересекает ось $y$ в точке $y = 1$.
• Однако важно отметить, что график не существует в точках $x = \frac{\pi}{2} + \pi n$, где $n$ — целое число. Это точки, в которых тангенс не существует.

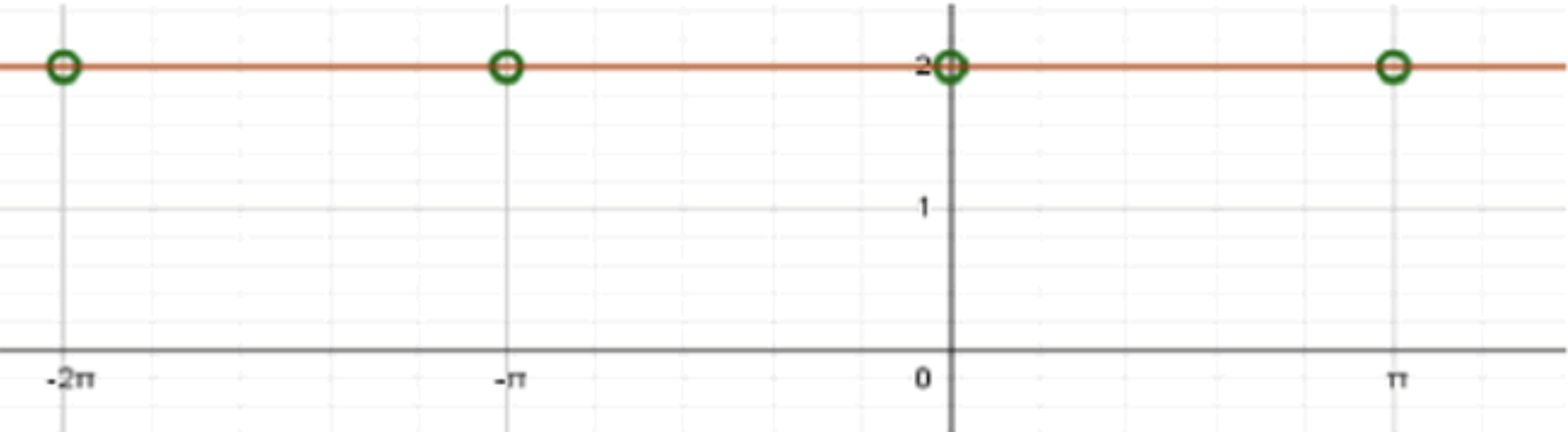
б) $y = 2\cos^2(\operatorname{ctg} x) + 2\sin^2(\operatorname{ctg} x) = 2$

Шаг 1: Анализ функции

Данная функция имеет вид:

$$y = 2\cos^2(\operatorname{ctg} x) + 2\sin^2(\operatorname{ctg} x)$$

Мы можем заметить, что выражение $\cos^2 \theta + \sin^2 \theta = 1$ — это основной тригонометрический тождество. Если заменить $\theta$ на $\operatorname{ctg} x$, то получим:

$$\cos^2(\operatorname{ctg} x) + \sin^2(\operatorname{ctg} x) = 1$$

Тогда функция принимает вид:

$$y = 2 \cdot 1 = 2$$

То есть, эта функция также является постоянной функцией, равной 2.

Шаг 2: Область определения

Для того чтобы функция $y = 2\cos^2(\operatorname{ctg} x) + 2\sin^2(\operatorname{ctg} x)$ была определена, нужно, чтобы $\operatorname{ctg} x$ существовал. Котангенс не существует в точках, где $\sin x = 0$, то есть:

$$x \neq \pi n$$

где $n$ — целое число. Это означает, что график функции будет существовать, за исключением точек $x = \pi n$, где котангенс не определен.

Шаг 3: Построение графика

• График функции $y = 2$ представляет собой горизонтальную прямую, которая пересекает ось $y$ в точке $y = 2$.
• Однако, как и в предыдущем случае, график не существует в точках $x = \pi n$, где $n$ — целое число, так как в этих точках котангенс не определен.