ГДЗ 10-11 Класс Номер 14.23 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y=\mathrm{tg}(\cos x)\cdot \mathrm{ctg}(\cos x)$

б) $y=-2\mathrm{tg}(\sin x)\cdot \mathrm{ctg}(\sin x)$

Построить график функции:

а) $y = \operatorname{tg}(\cos x) \cdot \operatorname{ctg}(\cos x) = 1$

Область определения:

$$\cos x_1 \neq \frac{\pi}{2} + \pi n;$$ $$\cos x_2 \neq \pi n;$$ $$\cos x \neq 0;$$ $$x \neq \frac{\pi}{2} + \pi n;$$

График функции:

б) $y = -2 \operatorname{tg}(\sin x) \cdot \operatorname{ctg}(\sin x) = -2$

Область определения:

$$\sin x_1 \neq \frac{\pi}{2} + \pi n;$$ $$\sin x_2 \neq \pi n;$$ $$\sin x \neq 0;$$ $$x \neq \pi n;$$

График функции:

а) $y = \operatorname{tg}(\cos x) \cdot \operatorname{ctg}(\cos x) = 1$

Шаг 1: Разбор функции

Функция имеет вид:

$$y = \operatorname{tg}(\cos x) \cdot \operatorname{ctg}(\cos x)$$

Рассмотрим выражение более детально.

• $\operatorname{tg}(\cos x) = \frac{\sin(\cos x)}{\cos(\cos x)}$
• $\operatorname{ctg}(\cos x) = \frac{\cos(\cos x)}{\sin(\cos x)}$

Теперь перемножим эти выражения:

$$y = \frac{\sin(\cos x)}{\cos(\cos x)} \cdot \frac{\cos(\cos x)}{\sin(\cos x)}$$

Как видно, множители $\sin(\cos x)$ и $\cos(\cos x)$ взаимно сокращаются, и остается:

$$y = 1$$

Таким образом, эта функция упрощается до константы $y = 1$.

Шаг 2: Область определения

Чтобы понимать область определения данной функции, нужно обратить внимание на особенности тангенса и котангенса.

• $\operatorname{tg}(\cos x)$ и $\operatorname{ctg}(\cos x)$ не определены в точках, где $\cos x = 0$, так как в этих точках значения синуса и косинуса становятся нулевыми, что приводит к делению на ноль.

Таким образом, для $\operatorname{tg}(\cos x)$ и $\operatorname{ctg}(\cos x)$ область определения будет ограничена точками, где $\cos x = 0$, то есть:

$$\cos x_1 \neq \frac{\pi}{2} + \pi n$$

где $n$ — целое число, так как $\cos x = 0$ в этих точках. Следовательно, область определения будет:

$$x \neq \frac{\pi}{2} + \pi n$$

Шаг 3: Построение графика

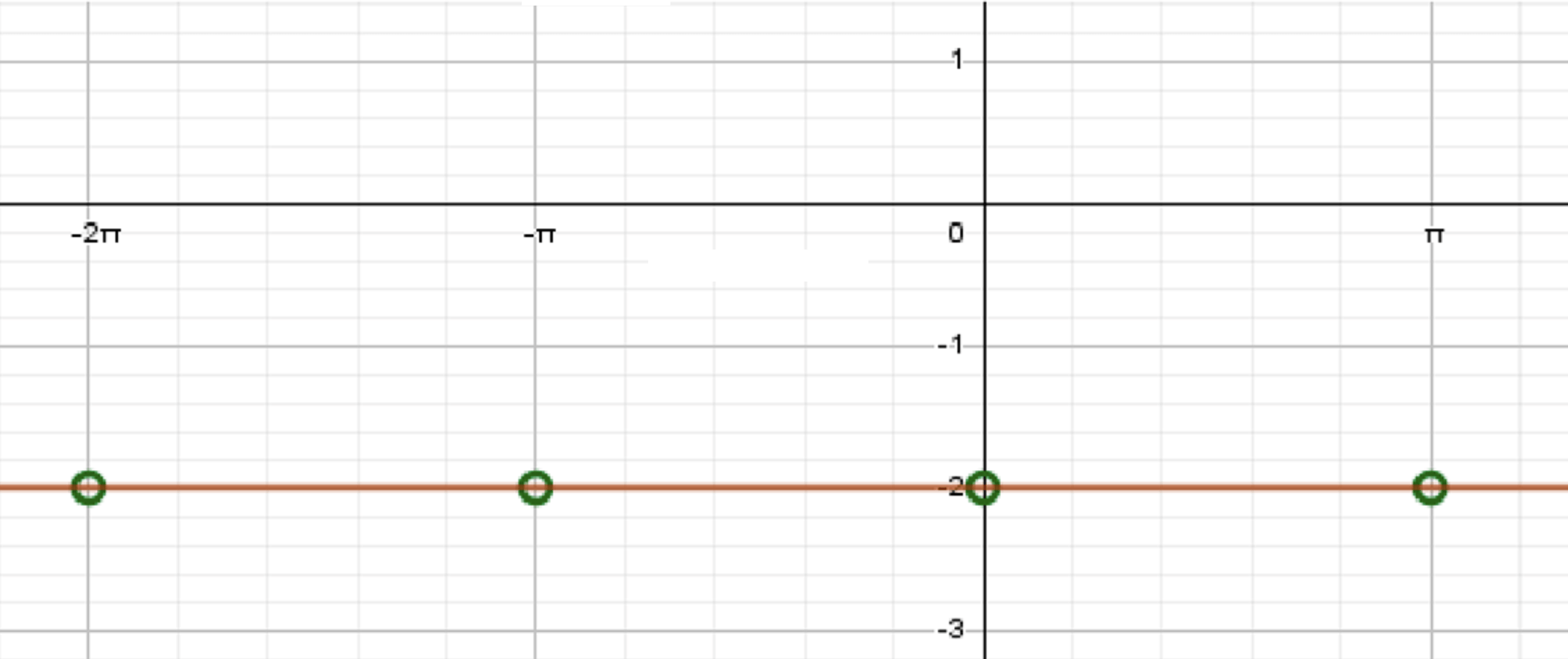
• График функции $y = 1$ представляет собой горизонтальную прямую, которая проходит через $y = 1$.
• Однако важно отметить, что функция не существует в точках $x = \frac{\pi}{2} + \pi n$, где $n$ — целое число, так как в этих точках функция не определена из-за значения $\cos x = 0$.

б) $y = -2 \operatorname{tg}(\sin x) \cdot \operatorname{ctg}(\sin x) = -2$

Шаг 1: Разбор функции

Рассмотрим функцию:

$$y = -2 \operatorname{tg}(\sin x) \cdot \operatorname{ctg}(\sin x)$$

Как и в предыдущем случае, нужно внимательно изучить произведение тангенса и котангенса.

• $\operatorname{tg}(\sin x) = \frac{\sin(\sin x)}{\cos(\sin x)}$
• $\operatorname{ctg}(\sin x) = \frac{\cos(\sin x)}{\sin(\sin x)}$

Перемножим эти выражения:

$$y = -2 \cdot \frac{\sin(\sin x)}{\cos(\sin x)} \cdot \frac{\cos(\sin x)}{\sin(\sin x)}$$

Как и в предыдущем случае, множители $\sin(\sin x)$ и $\cos(\sin x)$ взаимно сокращаются, и получается:

$$y = -2$$

Таким образом, функция упрощается до константы $y = -2$.

Шаг 2: Область определения

Аналогично предыдущей функции, для функции $y = -2 \operatorname{tg}(\sin x) \cdot \operatorname{ctg}(\sin x)$ необходимо учитывать точки, в которых $\sin x = 0$, так как котангенс и тангенс не определены при $\sin x = 0$. Это происходит в точках:

$$\sin x_1 \neq \frac{\pi}{2} + \pi n$$

и

$$\sin x_2 \neq \pi n$$

Таким образом, функция не определена в точках $x = \pi n$, где $n$ — целое число, так как в этих точках $\sin x = 0$.

Шаг 3: Построение графика

• График функции $y = -2$ представляет собой горизонтальную прямую, которая проходит через $y = -2$.
• Однако важно отметить, что функция не существует в точках $x = \pi n$, где $n$ — целое число, так как в этих точках функция не определена из-за значения $\sin x = 0$.