ГДЗ 10-11 Класс Номер 14.3 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Решите графически уравнение:

а) $\operatorname{tg} x = -\sqrt{3}$;

б) $\operatorname{tg} x = 1$;

в) $\operatorname{tg} x = -1$;

г) $\operatorname{tg} x = 0$

Решить графически уравнение:

а) $\operatorname{tg} x = -\sqrt{3}$;

Построим графики функций $y = \operatorname{tg} x$ и $y = -\sqrt{3}$:

Графики пересекаются в точке: $x = -\frac{\pi}{3}$;

Расстояние между соседними точками равно $\pi$;

Ответ: $x = -\frac{\pi}{3} + \pi n$.

б) $\operatorname{tg} x = 1$;

Построим графики функций $y = \operatorname{tg} x$ и $y = 1$:

Графики пересекаются в точке: $x = \frac{\pi}{4}$;

Расстояние между соседними точками равно $\pi$;

Ответ: $x = \frac{\pi}{4} + \pi n$.

в) $\operatorname{tg} x = -1$;

Построим графики функций $y = \operatorname{tg} x$ и $y = -1$:

Графики пересекаются в точке: $x = -\frac{\pi}{4}$;

Расстояние между соседними точками равно $\pi$;

Ответ: $x = -\frac{\pi}{4} + \pi n$.

г) $\operatorname{tg} x = 0$;

Построим график функции $y = \operatorname{tg} x$:

График пересекает ось абсцисс в точке: $x = 0$;

Расстояние между соседними точками равно $\pi$;

Ответ: $x = \pi n$.

Решим графически уравнения:

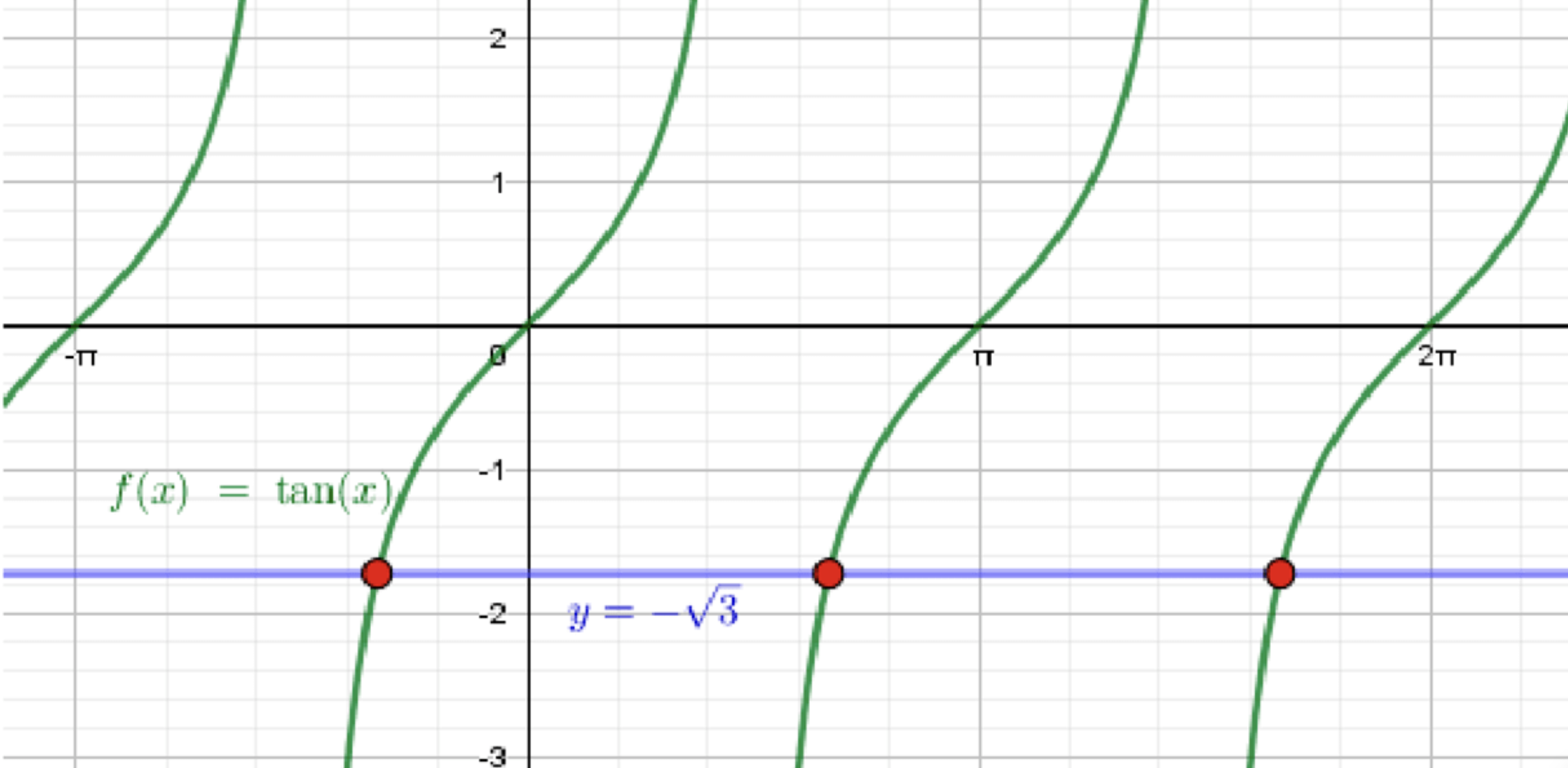
а) $\operatorname{tg} x = -\sqrt{3}$;

Построение графиков функций:

• График функции $y = \operatorname{tg} x$ — это стандартная тангенсная функция, которая имеет вертикальные асимптоты в точках $x = \frac{\pi}{2} + n\pi$ (где $n$ — целое число), а также проходит через точки $x = n\pi$ с амплитудой, которая изменяется от $-\infty$ до $+\infty$.
• График функции $y = -\sqrt{3}$ — это горизонтальная прямая, расположенная на уровне $y = -\sqrt{3}$, которая пересекает ось $y$ в точке $-\sqrt{3}$.

Поиск точек пересечения:

• Чтобы найти точку пересечения графиков функции $y = \operatorname{tg} x$ и прямой $y = -\sqrt{3}$, нужно понять, при каких значениях $x$ тангенс принимает значение $-\sqrt{3}$.
• Мы знаем, что тангенс принимает значения $\pm \sqrt{3}$ в следующих точках:
  • $\operatorname{tg} \left( \frac{\pi}{3} \right) = \sqrt{3}$,
  • $\operatorname{tg} \left( -\frac{\pi}{3} \right) = -\sqrt{3}$.
• Следовательно, первая точка пересечения будет $x = -\frac{\pi}{3}$.

График функции $y = \operatorname{tg} x$ — периодичен:

• График функции $y = \operatorname{tg} x$ имеет период $\pi$, то есть каждые $\pi$ единиц на оси $x$ будет повторяться та же форма графика.
• Это значит, что следующая точка пересечения будет на $x = -\frac{\pi}{3} + \pi n$, где $n$ — целое число.

Ответ:

• Все решения уравнения $\operatorname{tg} x = -\sqrt{3}$ будут выражаться формулой:

  $$x = -\frac{\pi}{3} + \pi n$$

  где $n$ — целое число.

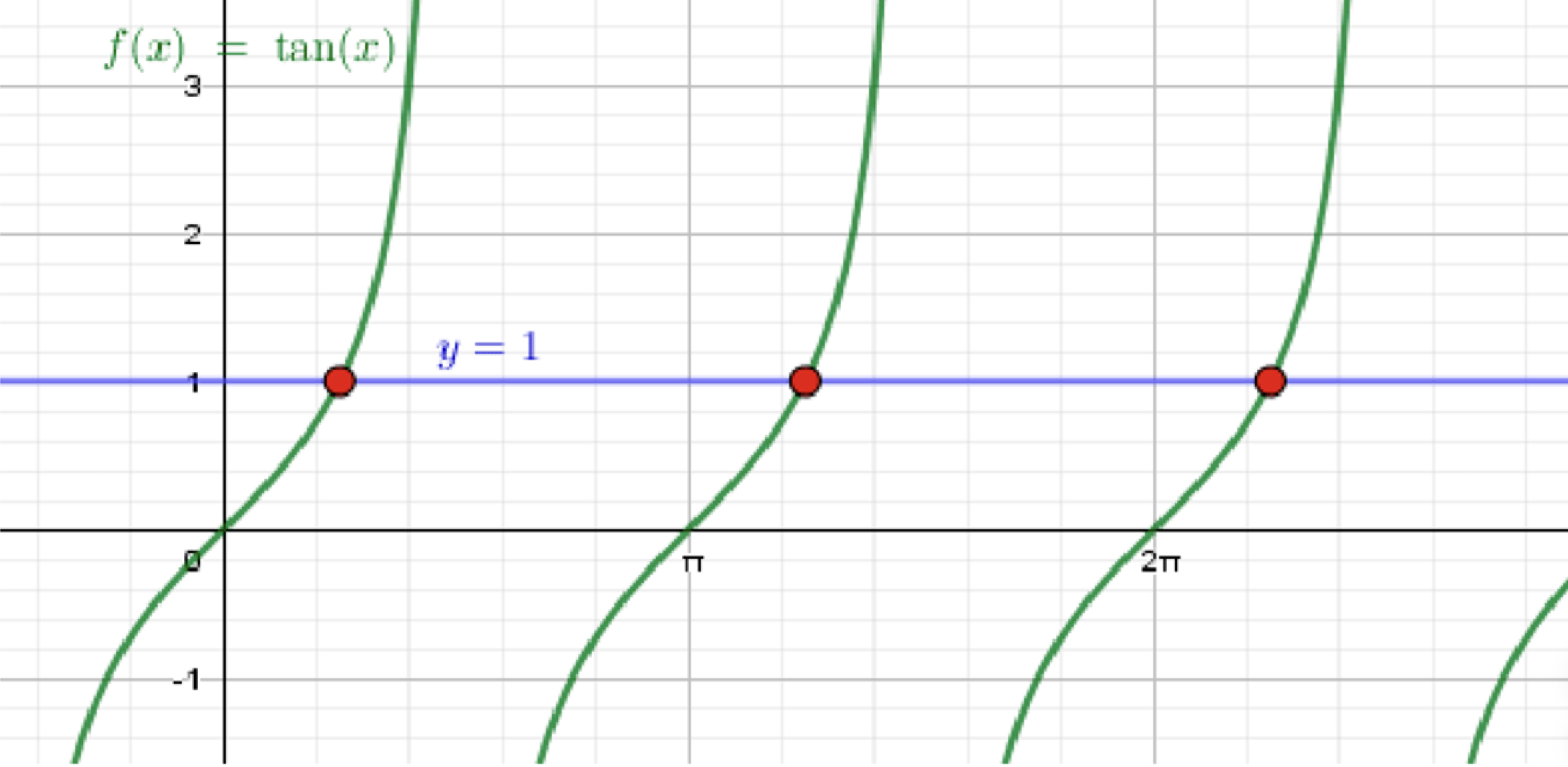
б) $\operatorname{tg} x = 1$;

Построение графиков функций:

• График функции $y = \operatorname{tg} x$ остается таким же, как и в предыдущем пункте.
• График функции $y = 1$ — это горизонтальная прямая, расположенная на уровне $y = 1$, которая пересекает ось $y$ в точке $1$.

Поиск точек пересечения:

• Чтобы найти точки пересечения, нужно определить, при каких значениях $x$ тангенс принимает значение 1.
• Мы знаем, что $\operatorname{tg} \left( \frac{\pi}{4} \right) = 1$.
• Следовательно, первая точка пересечения будет $x = \frac{\pi}{4}$.

График функции $y = \operatorname{tg} x$ — периодичен:

• Период функции $y = \operatorname{tg} x$ снова составляет $\pi$, то есть каждый $\pi$ будет повторяться та же форма графика.
• Таким образом, следующая точка пересечения будет на $x = \frac{\pi}{4} + \pi n$, где $n$ — целое число.

Ответ:

• Все решения уравнения $\operatorname{tg} x = 1$ будут выражаться формулой:

  $$x = \frac{\pi}{4} + \pi n$$

  где $n$ — целое число.

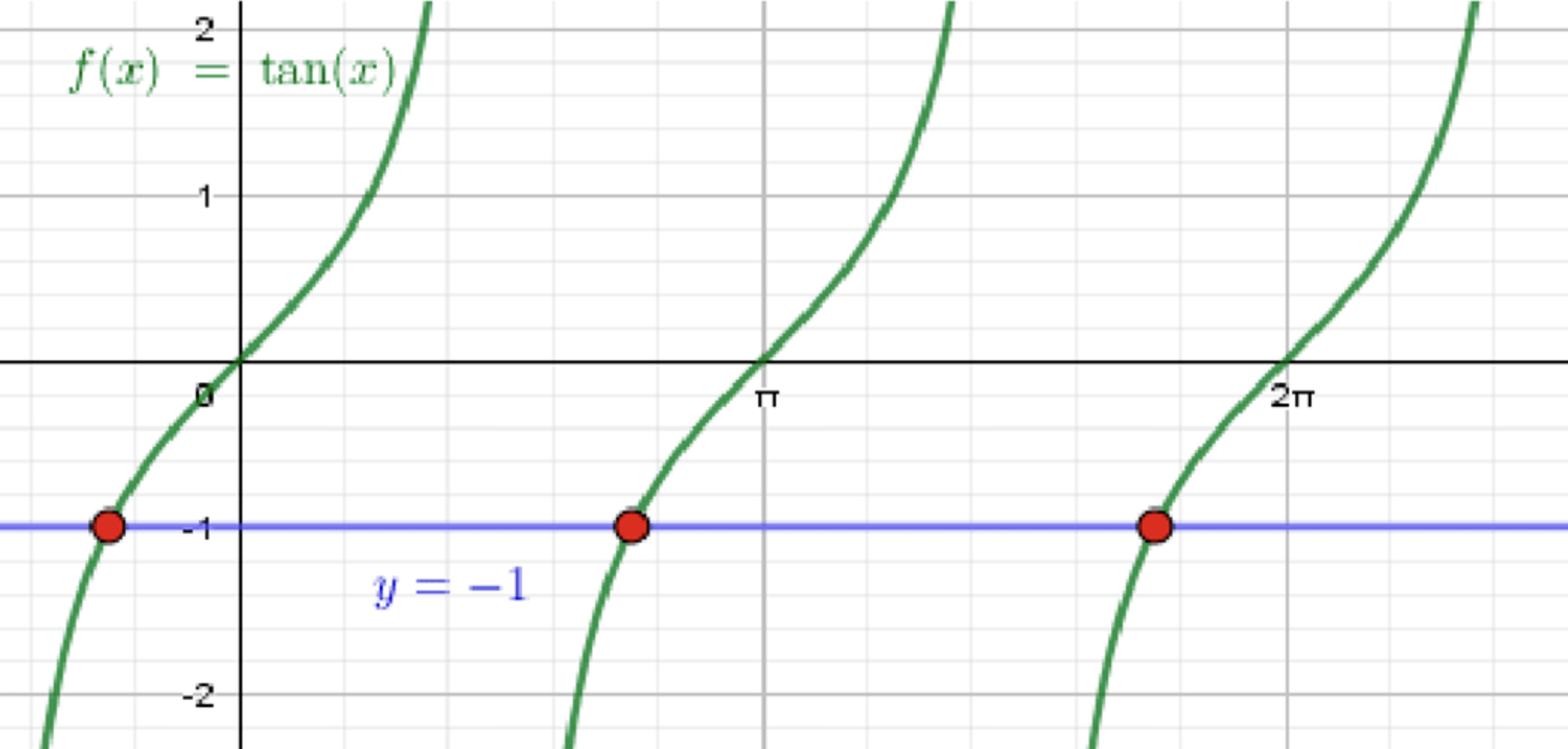
в) $\operatorname{tg} x = -1$;

Построение графиков функций:

• График функции $y = \operatorname{tg} x$ сохраняет прежнюю форму.
• График функции $y = -1$ — это горизонтальная прямая, расположенная на уровне $y = -1$, которая пересекает ось $y$ в точке $-1$.

Поиск точек пересечения:

• Нужно найти, при каких значениях $x$ тангенс принимает значение $-1$.
• Мы знаем, что $\operatorname{tg} \left( -\frac{\pi}{4} \right) = -1$.
• Следовательно, первая точка пересечения будет $x = -\frac{\pi}{4}$.

График функции $y = \operatorname{tg} x$ — периодичен:

• Период функции $y = \operatorname{tg} x$ также равен $\pi$.
• Это означает, что следующая точка пересечения будет на $x = -\frac{\pi}{4} + \pi n$, где $n$ — целое число.

Ответ:

• Все решения уравнения $\operatorname{tg} x = -1$ будут выражаться формулой:

  $$x = -\frac{\pi}{4} + \pi n$$

  где $n$ — целое число.

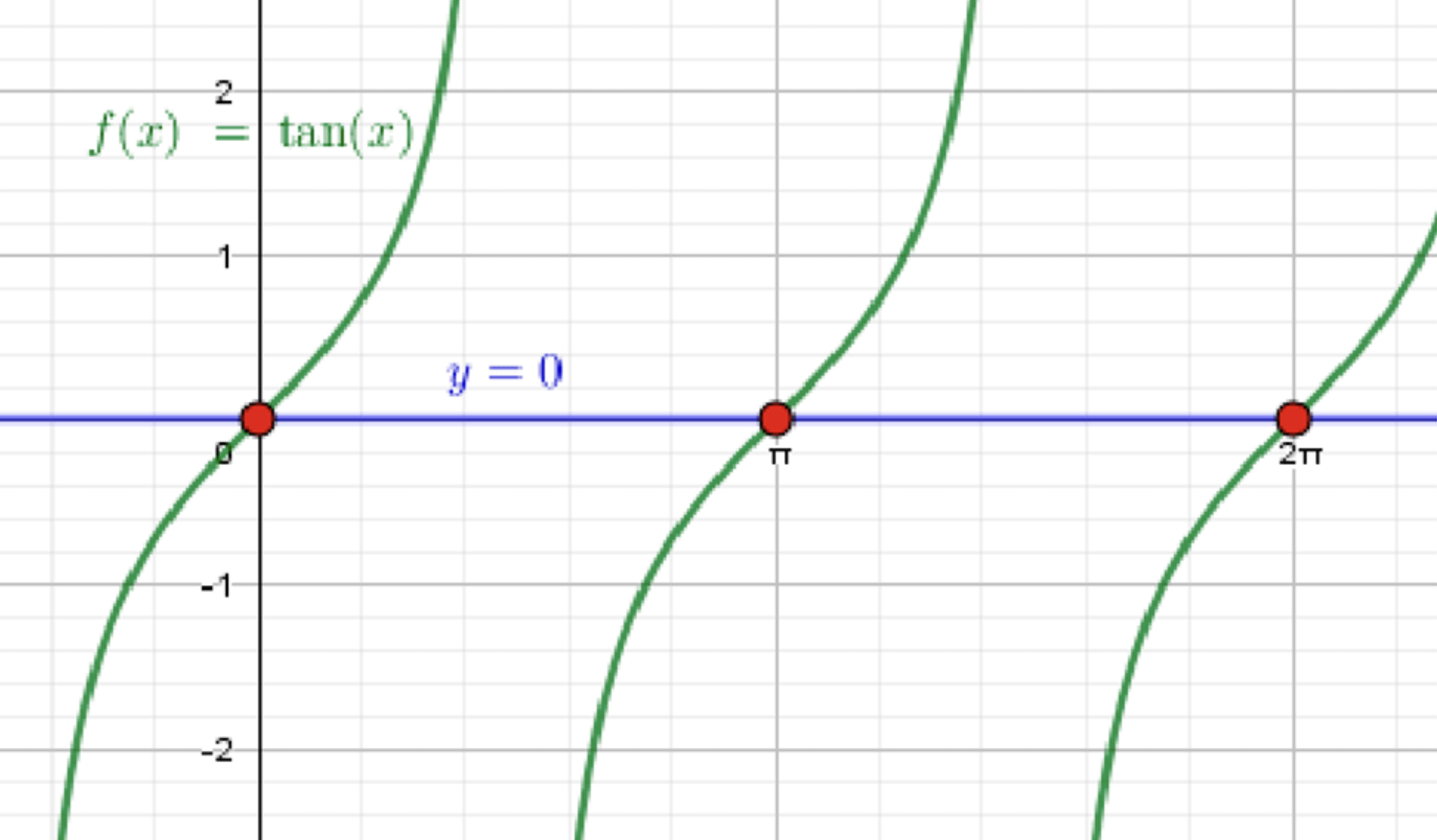
г) $\operatorname{tg} x = 0$;

Построение графиков функций:

• График функции $y = \operatorname{tg} x$ остается стандартным.
• График функции $y = 0$ — это горизонтальная прямая, которая совпадает с осью абсцисс, $y = 0$.

Поиск точек пересечения:

• Для нахождения точек пересечения нужно определить, при каких значениях $x$ тангенс равен нулю.
• Тангенс равен нулю в точках $x = n\pi$, где $n$ — целое число.
• Следовательно, первая точка пересечения будет $x = 0$.

График функции $y = \operatorname{tg} x$ — периодичен:

• Период функции $y = \operatorname{tg} x$ составляет $\pi$, поэтому следующие точки пересечения будут на $x = \pi n$, где $n$ — целое число.

Ответ:

• Все решения уравнения $\operatorname{tg} x = 0$ будут выражаться формулой:

  $$x = \pi n$$

  где $n$ — целое число.

Итоговые ответы:

а) $x = -\frac{\pi}{3} + \pi n$

б) $x = \frac{\pi}{4} + \pi n$

в) $x = -\frac{\pi}{4} + \pi n$

г) $x=\pi n$