Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 14.6 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Решите графически уравнение:
а) ;
б) ;
в) ;
г)
Решить графически уравнение:
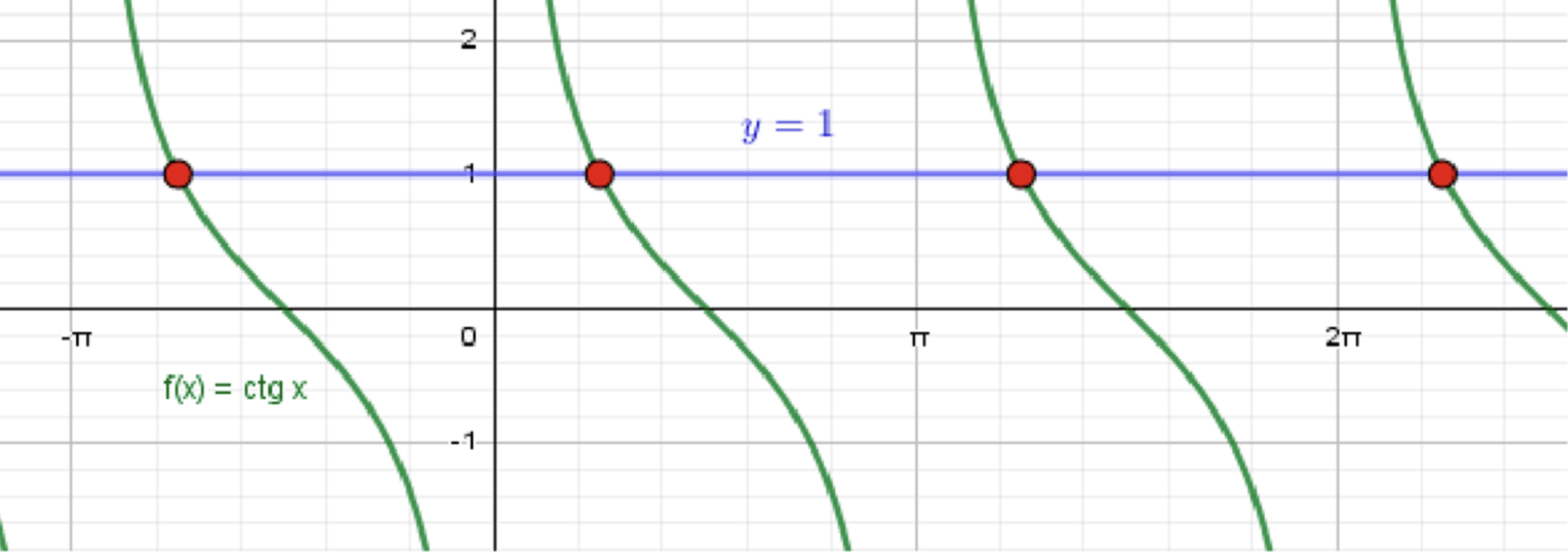
а) ;
Построим графики функций и :
Графики пересекаются в точке: ;
Расстояние между соседними точками равно ;
Ответ: .
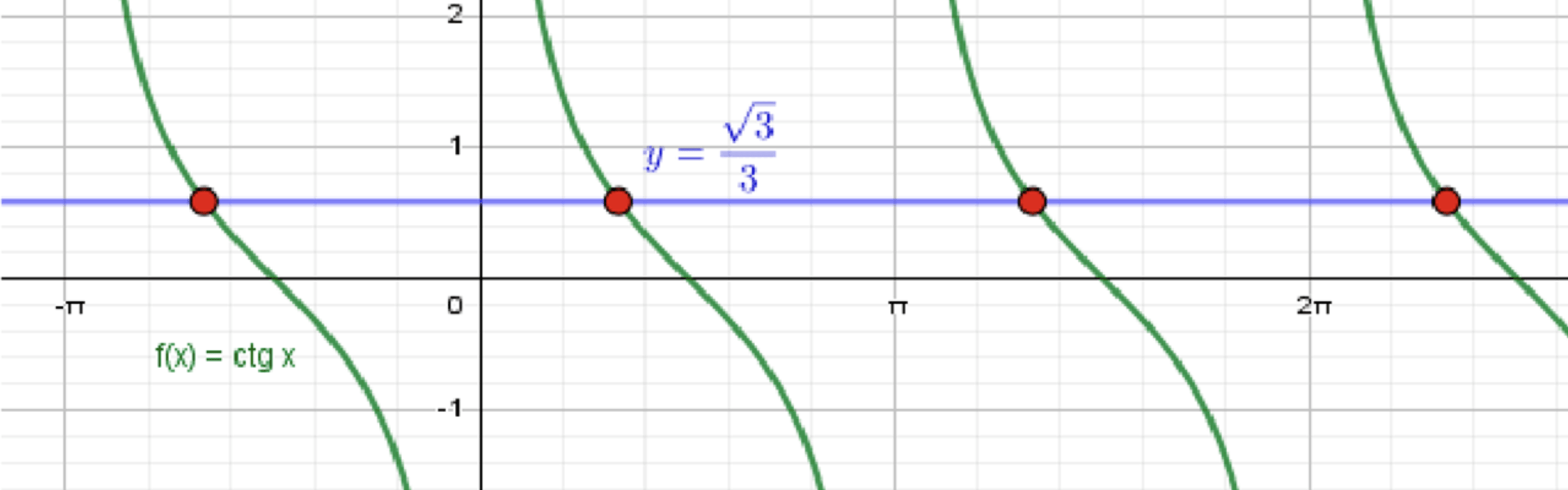
б) ;
Построим графики функций и :
Графики пересекаются в точке: ;
Расстояние между соседними точками равно ;
Ответ: .
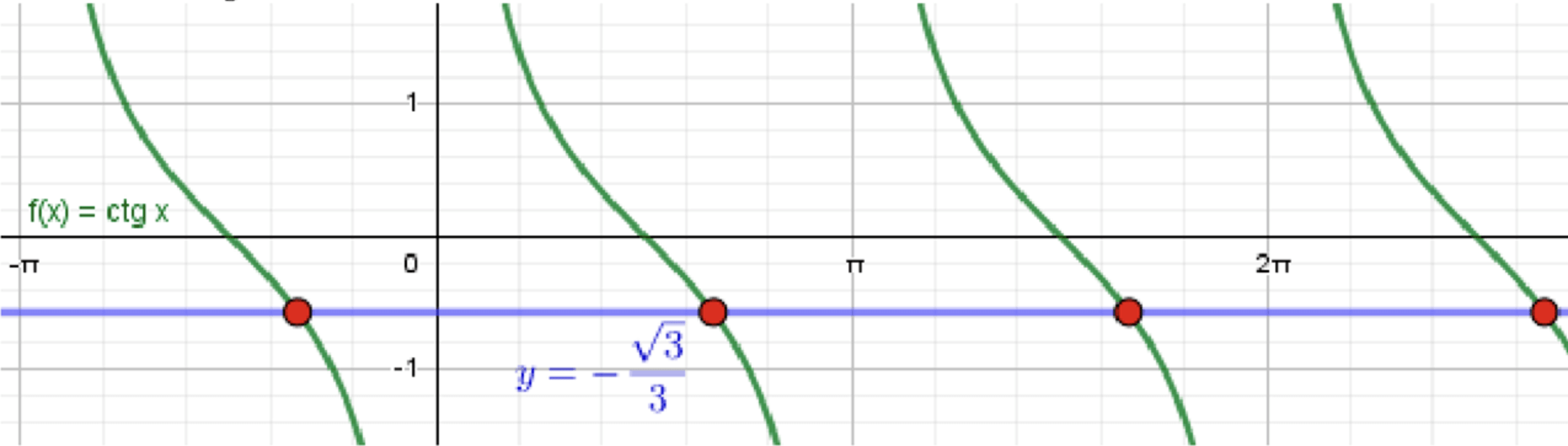
в) ;
Построим графики функций и :
Графики пересекаются в точке: ;
Расстояние между соседними точками равно ;
Ответ: .
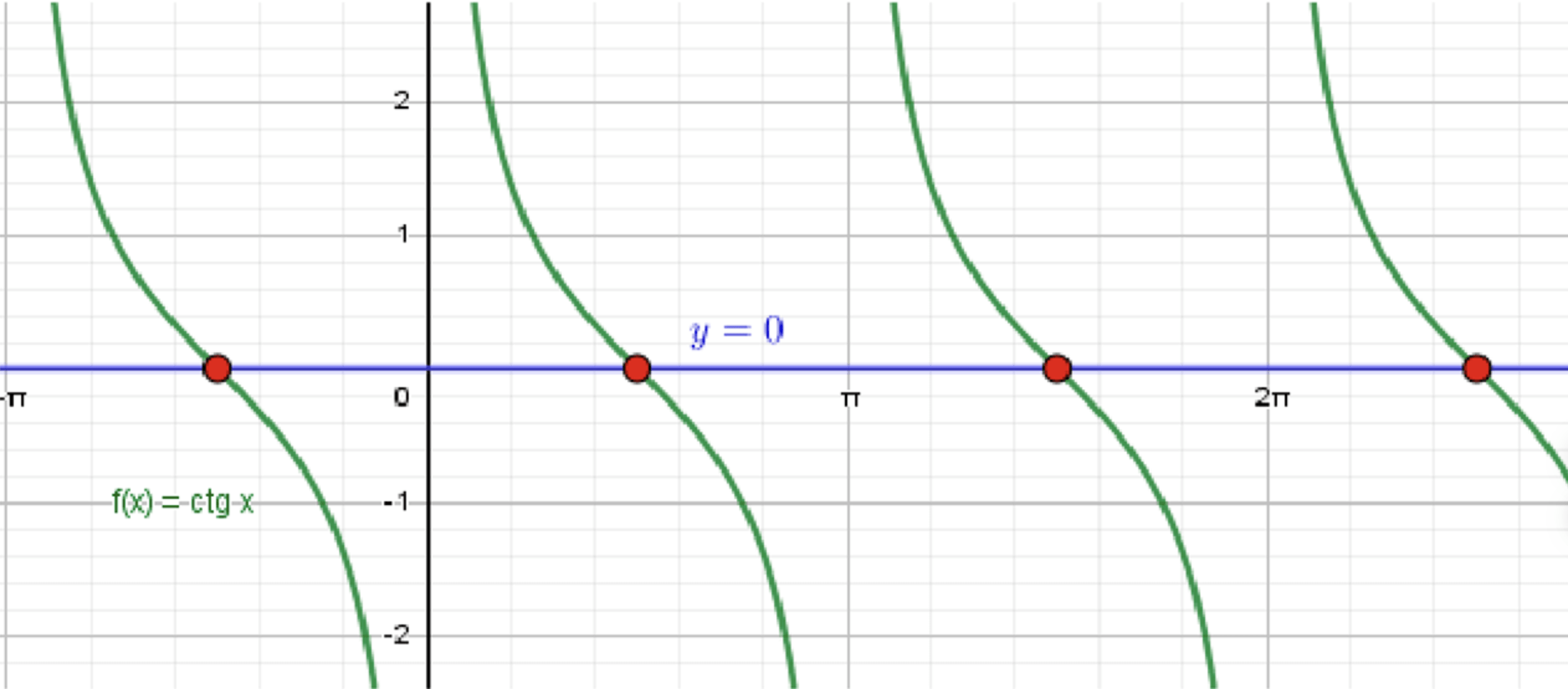
г) ;
Построим график функции :
График пересекает ось абсцисс в точке: ;
Расстояние между соседними точками равно ;
Ответ: .
а)
Запишем уравнение:
Котангенс функции является отношением косинуса к синусу:
Таким образом, уравнение можно переписать как:
Это равенство выполняется, когда .
Решение уравнения :
Для решения уравнения , можно воспользоваться тем, что:
где — целое число, так как период функции равен .
Графический подход:
Построим графики функций и . График функции — это периодическая кривая с вертикальными асимптотами в точках , где — целое число, и с периодом . График функции — это горизонтальная прямая, пересекающая ось .
Пересечение графиков:
Графики функций и пересекаются в точках, где . Таким образом, решение уравнения:
Ответ: .
б)
Запишем уравнение:
Аналогично предыдущему шагу, у нас есть уравнение:
Решение уравнения:
Это уравнение выполняется, когда:
Зная, что , получаем:
Графический подход:
Построим графики функций и . График функции имеет период и вертикальные асимптоты в точках . Прямая пересечет график функции в точках .
Ответ: .
в)
Запишем уравнение:
Это уравнение выполняется, когда:
Зная, что , получаем:
Графический подход:
Построим графики функций и . График функции будет пересекаться с горизонтальной прямой в точке , где — целое число.
Ответ: .
г)
Запишем уравнение:
Это уравнение выполняется, когда:
Решение уравнения:
Значение происходит в точках:
Графический подход:
Построим график функции , который будет пересекать ось абсцисс в точках, где , а именно в точке .
Ответ: .
Итоговые ответы:
а)
б)
в)
г)