ГДЗ 10-11 Класс Номер 15.16 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \arccos x + \arccos(-x)$;

б) $y = \cos(\arccos x) = x$

Построить график функции:

а) $y = \arccos x + \arccos(-x)$;

$y = \arccos x + \pi — \arccos x = \pi$;

Область определения:

$-1 \leq x \leq 1$;

График функции:

б) $y = \cos(\arccos x) = x$;

Область определения:

$-1 \leq x \leq 1$;

График функции:

а) $y = \arccos x + \arccos(-x)$

Шаг 1: Упростим выражение для функции

Мы начинаем с функции:

$$y = \arccos x + \arccos(-x)$$

Воспользуемся известным свойством арккосинуса, что $\arccos(-x) = \pi — \arccos(x)$. Это свойство следует из того, что косинус угла $\alpha$ и $\pi — \alpha$ равны по величине, но противоположны по знаку.

Подставляем это в исходное выражение:

$$y = \arccos x + \pi — \arccos x$$

Мы видим, что $\arccos x$ и $-\arccos x$ взаимно сокращаются:

$$y = \pi$$

Таким образом, независимо от значения $x$ на области определения, результат всегда равен $\pi$.

Шаг 2: Область определения

Арккосинус $\arccos x$ определен для значений $x$ в интервале $[-1, 1]$. Это означает, что область определения функции $y = \arccos x + \arccos(-x)$ также будет $-1 \leq x \leq 1$.

Шаг 3: Интерпретация графика

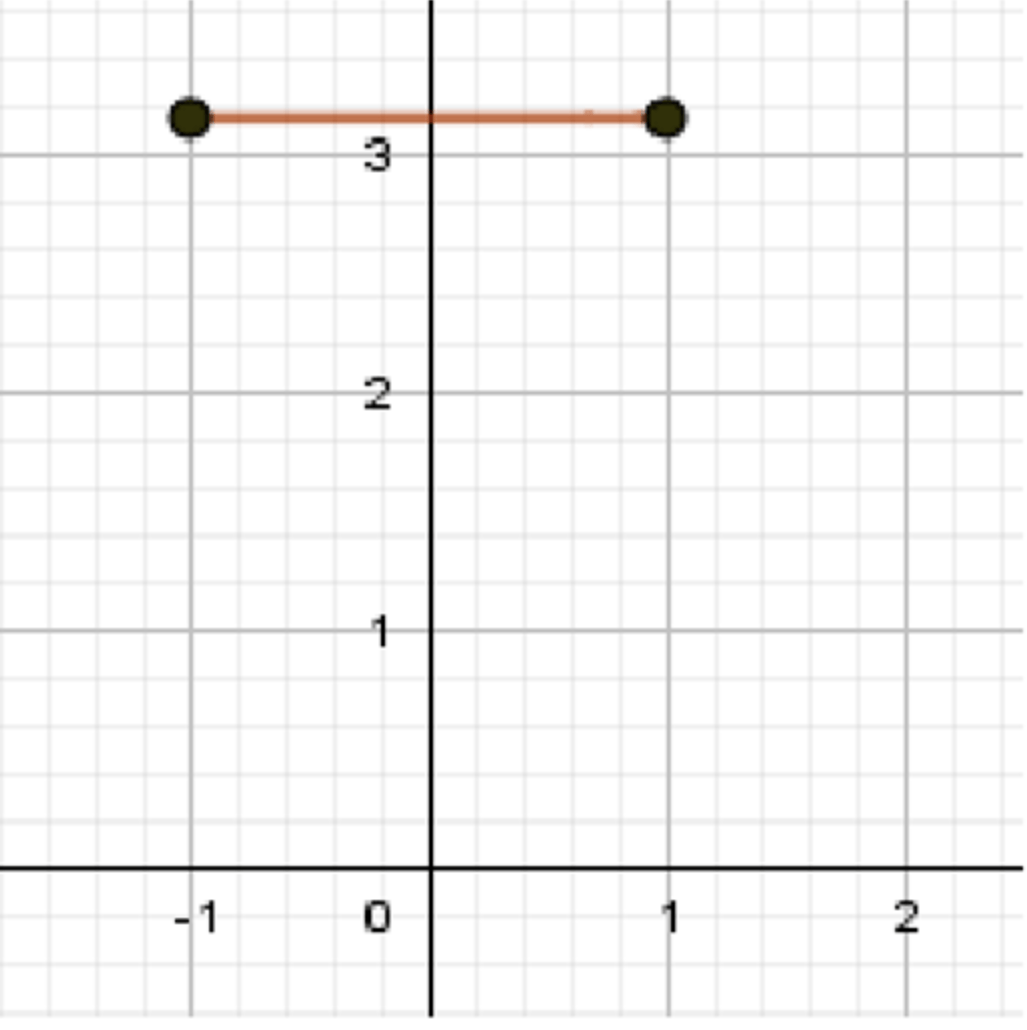
Поскольку $y = \pi$ для всех значений $x$ из области определения, график функции будет горизонтальной прямой, расположенной на уровне $y = \pi$.

Функция $y = \arccos x + \arccos(-x)$ принимает постоянное значение $\pi$ для всех $x$ в области определения $[-1; 1]$. График функции — это горизонтальная прямая, расположенная на уровне $y = \pi$.

б) $y = \cos(\arccos x) = x$

Шаг 1: Разбор функции

Мы имеем функцию:

$$y = \cos(\arccos x)$$

Известно, что $\cos(\arccos x) = x$, поскольку арккосинус и косинус являются обратными функциями друг друга. То есть, если $y = \arccos x$, то $\cos(\arccos x) = x$.

Таким образом, функция упрощается до:

$$y = x$$

Шаг 2: Область определения

Арккосинус $\arccos x$ определен для $x \in [-1, 1]$, следовательно, область определения функции $y = \cos(\arccos x)$ также будет $-1 \leq x \leq 1$.

Шаг 3: Интерпретация графика

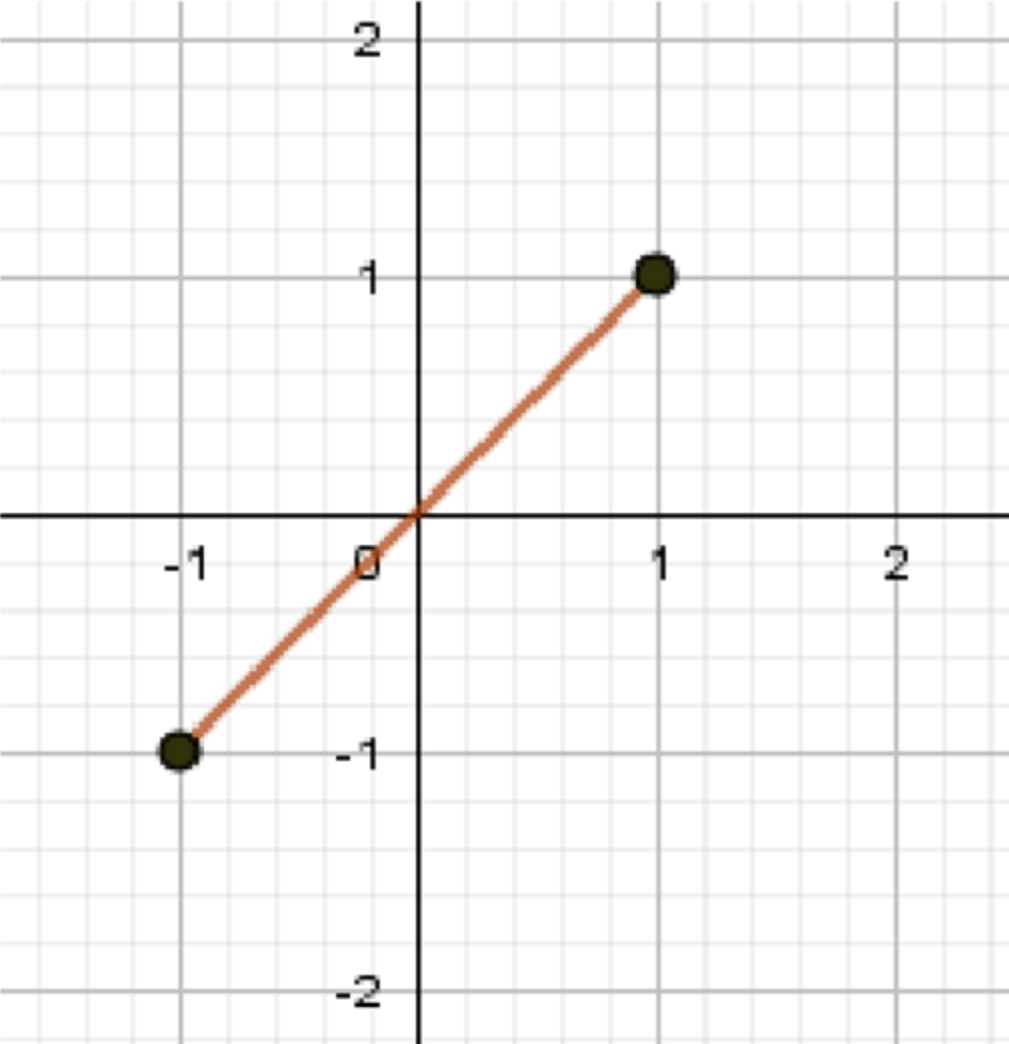
Функция $y = x$ — это линейная функция с угловым коэффициентом 1. На интервале $[-1, 1]$ график этой функции будет прямой, проходящей через начало координат (0, 0) с наклоном 45 градусов.

График функции $y = \cos(\arccos x) = x$ — это прямая, проходящая через начало координат с угловым коэффициентом 1. Интервал определения: $-1 \leq x \leq 1$.