Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 16.13 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Сколько корней имеет заданное уравнение на заданном промежутке:
а)
б)
Сколько корней имеет заданное уравнение на заданном промежутке:
а)
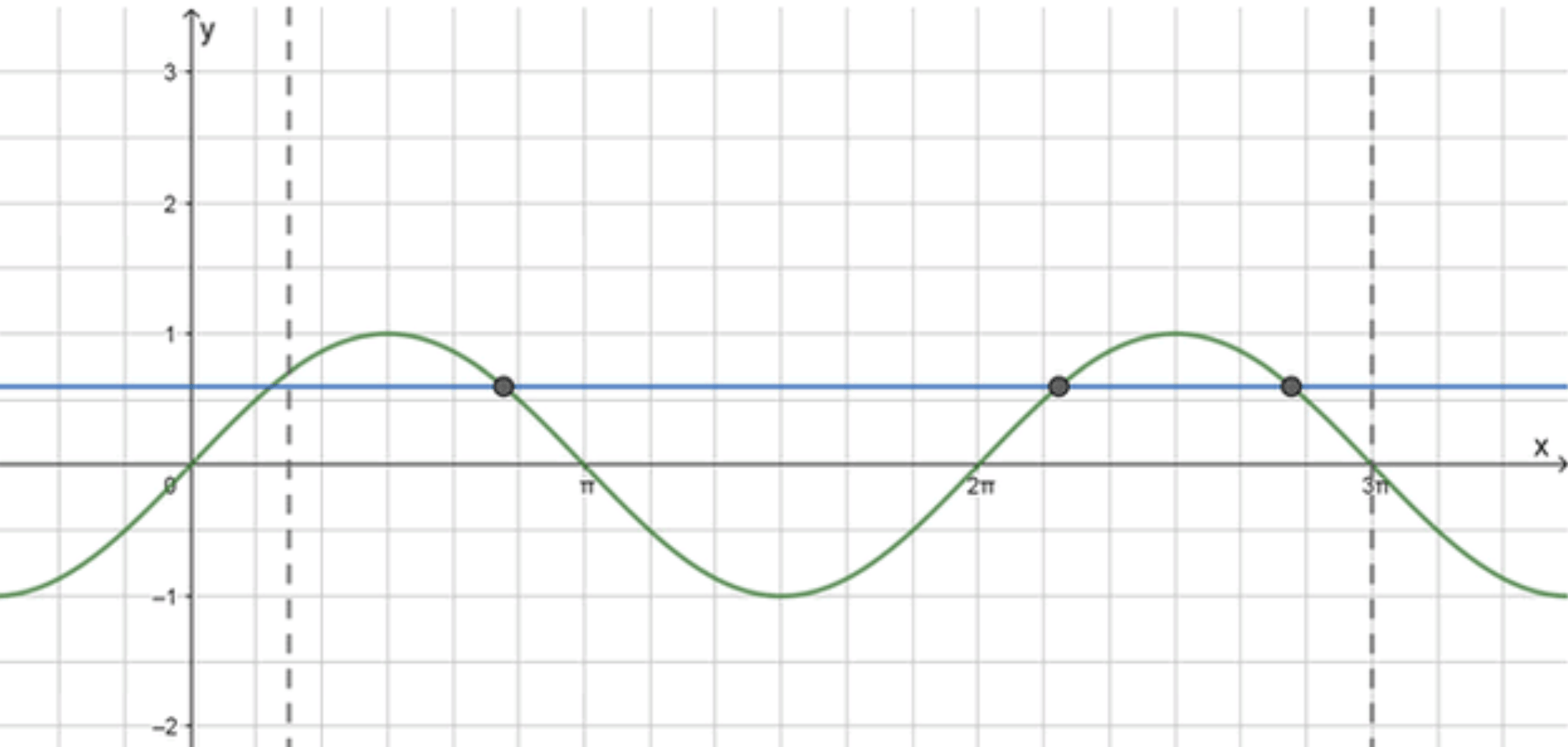
Построим графики функций и :
Ответ: 3.
б)
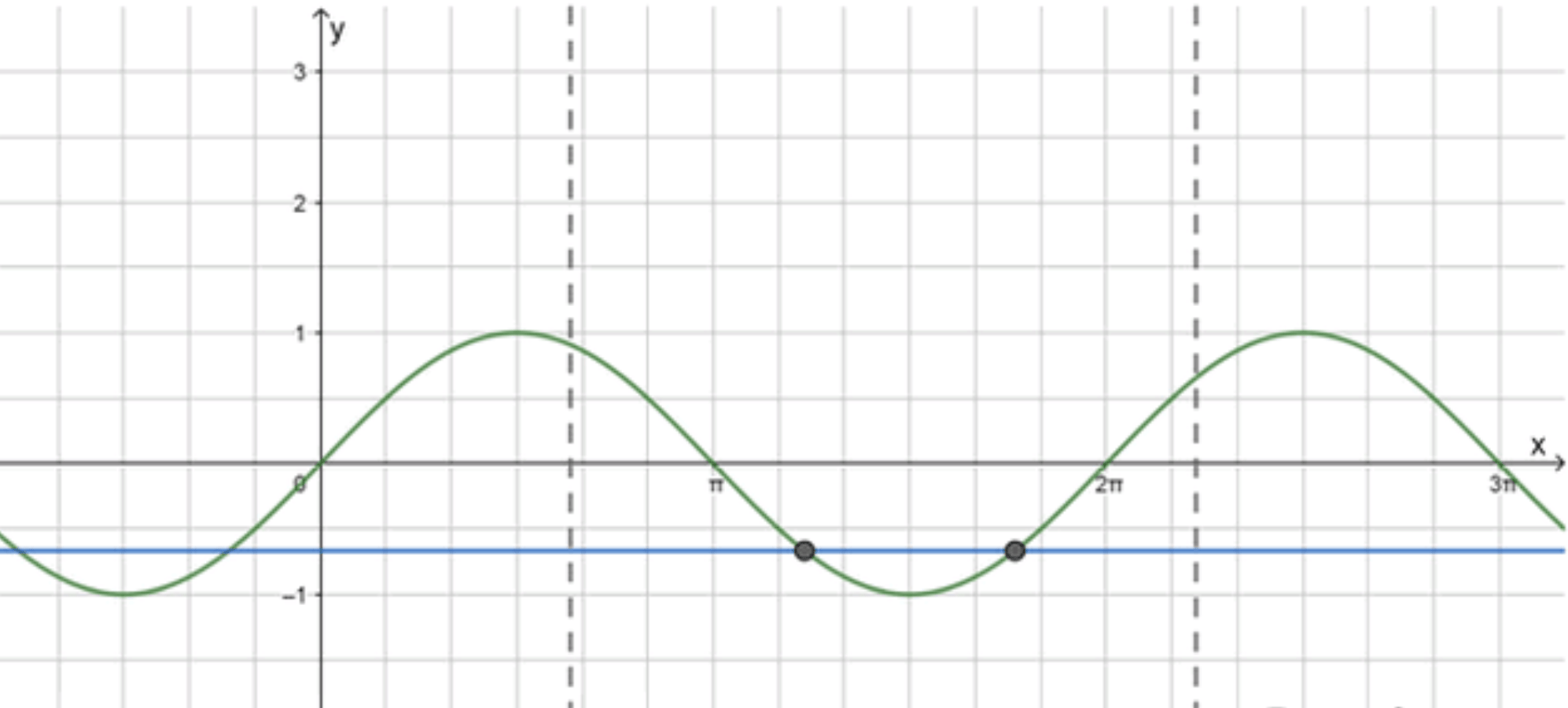
Построим графики функций и :
Ответ: 2.
а)
Понимание уравнения:
Нам нужно найти количество корней уравнения на промежутке . Это значит, что мы должны найти, сколько раз график функции пересекает горизонтальную линию на этом промежутке.
График функции :
График функции — это периодическая волна с периодом , которая колеблется между значениями и . Мы знаем, что синус проходит через значения дважды за один период (в первой и второй половине периода), если значение лежит в пределах диапазона функции синуса.
Решение уравнения :
Для нахождения корней на промежутке , рассмотрим основное решение уравнения в интервале . Это можно решить через арксинус:
Численно . Это первое решение в интервале .
Вторая точка, где синус равен , будет на верхней полупериоде . Это решение можно найти как:
Теперь рассмотрим промежуток . Мы видим, что отрезок охватывает более одного периода синуса. Так как имеет период , и мы знаем, что на каждом периоде синус пересекает линию дважды, можем ожидать два пересечения на интервале и одно пересечение на интервале .
Ответ:
Количество корней на интервале равно 3.
Ответ: 3.
б)
Понимание уравнения:
Мы ищем количество корней уравнения на промежутке .
График функции :
График функции также периодичен с периодом , и его значения лежат в интервале от до . Мы ищем, сколько раз график синуса пересекает горизонтальную линию на промежутке .
Решение уравнения :
Для нахождения корней уравнения на интервале , рассмотрим решение уравнения . Это уравнение имеет два решения на каждом периоде синуса. Мы можем найти основное решение через арксинус:
Численно . Однако это значение не лежит на интервале , так как оно лежит в интервале .
Следовательно, нужно найти два угла, где синус равен , на интервале . Это будет:
Значения на интервале :
Эти значения лежат на интервале , так как они оба находятся в пределах .
Поэтому на интервале существует два пересечения функции с линией .
Ответ:
Количество корней на интервале равно 2.
Ответ: 2.