Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 16.14 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Сколько корней имеет заданное уравнение на заданном промежутке:
а) ;
б)
Сколько корней имеет заданное уравнение на заданном промежутке:
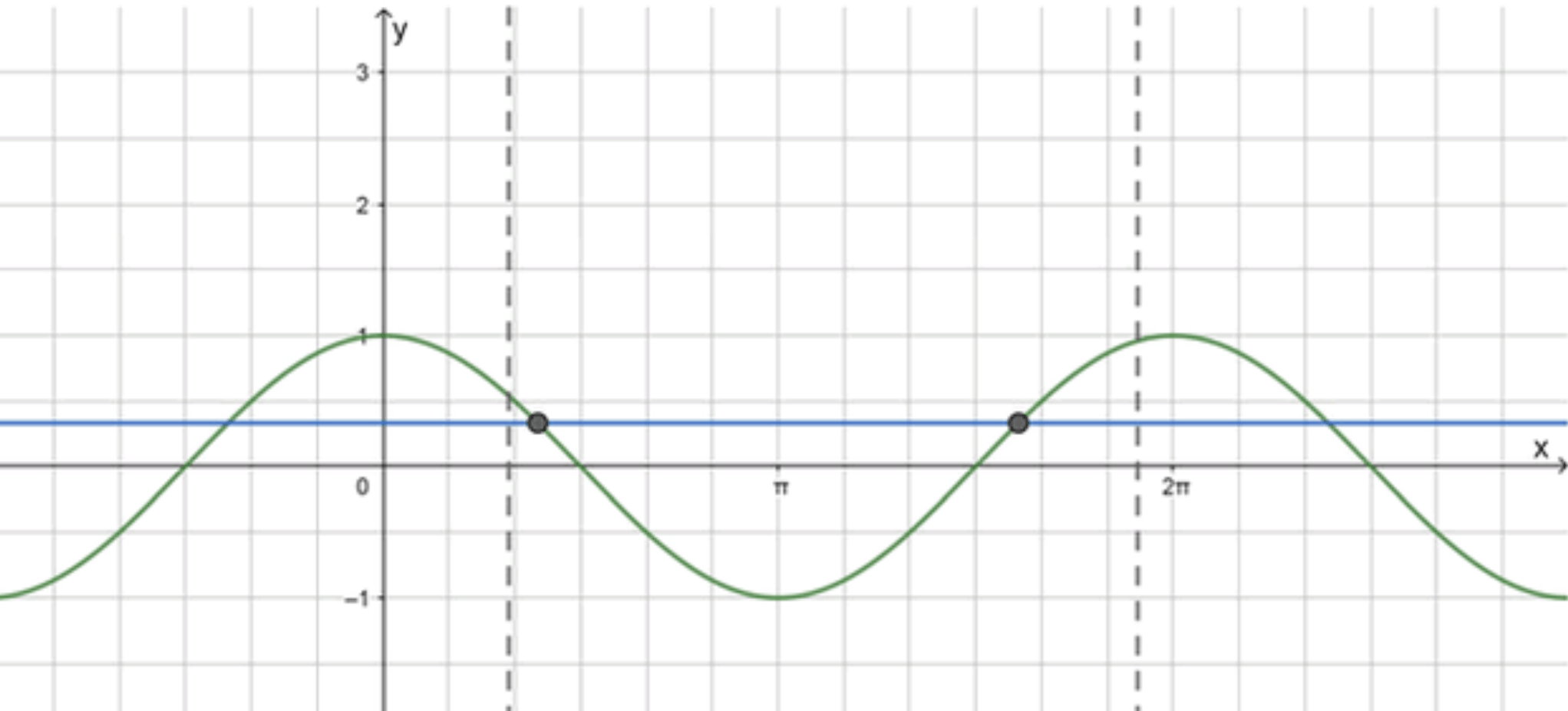
а) ;
Построим графики функций и :
Ответ: 2.
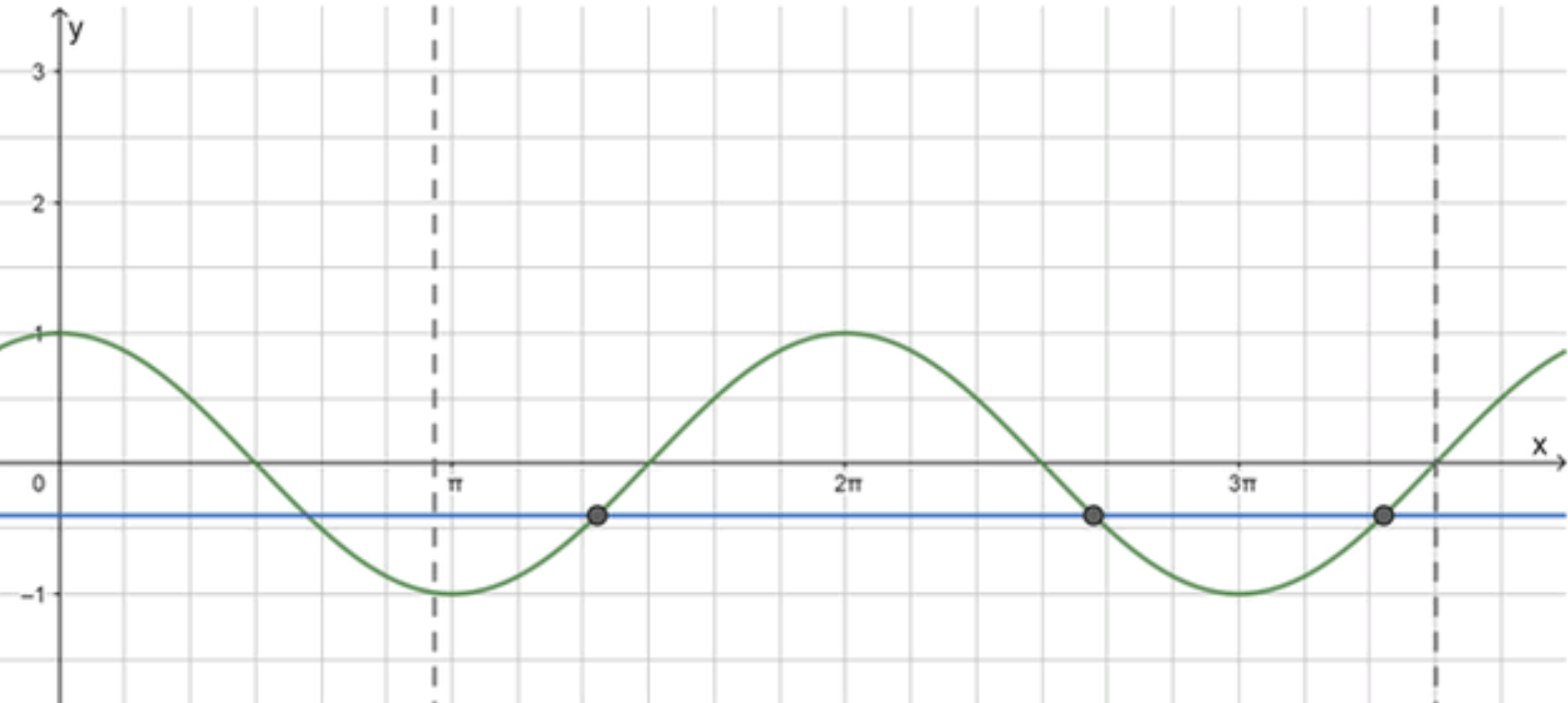
б) ;
Построим графики функций и :
Ответ: 3.
Сколько корней имеет заданное уравнение на заданном промежутке:
а)
1. Анализ уравнения:
Мы должны найти, сколько корней имеет уравнение на промежутке . Для этого нам нужно исследовать, как ведет себя график функции на этом промежутке и где он пересекает горизонтальную прямую .
2. Свойства функции :
- Функция — периодическая, с периодом , то есть .
- Значения функции находятся в интервале от до для всех . То есть .
- График функции имеет форму волны, которая колеблется между значениями и , и пересекает прямую на каждом цикле.
3. Найдем, где график функции пересекает прямую :
Для начала определим значения , при которых . Это уравнение можно решить с помощью обратной функции :
Посчитаем:
Поскольку функция периодична с периодом , решение уравнения будет повторяться через каждый период . Поэтому следующий корень можно найти, прибавив к найденному значению:
4. Проверка на интервале :
- Первый корень лежит в интервале .
- Второй корень также лежит в этом интервале.
5. Ответ:
Таким образом, на интервале у уравнения есть два корня.
Ответ: 2.
б)
1. Анализ уравнения:
Теперь нам нужно найти, сколько корней имеет уравнение на промежутке . Для этого опять-таки исследуем график функции и прямой на данном интервале.
2. Свойства функции :
Как и в предыдущем случае, функция имеет период , а значения функции лежат в интервале от до .
3. Найдем, где график функции пересекает прямую :
Для решения уравнения , используем обратную функцию :
Посчитаем:
Это значение является одним из корней, но оно находится за пределами нашего интервала , так как меньше 3. Поэтому нам нужно найти следующие корни.
Функция имеет период , следовательно, следующий корень можно найти, прибавив к найденному значению:
Следующий корень находится через один период:
4. Проверка на интервале :
- Первый корень лежит в интервале .
- Второй корень также лежит в интервале .
5. Ответ:
Таким образом, на интервале у уравнения есть три корня.
Ответ: 3.