ГДЗ 10-11 Класс Номер 17.14 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \arccos(2x) + \arccos(-2x)$;

б) $y = \arccos \frac{1}{x} + \arccos \left( -\frac{1}{x} \right)$;

в) $y = \operatorname{arcctg} x + \operatorname{arcctg}(-x)$;

г) $y = \operatorname{arcctg} \sqrt{x} + \operatorname{arcctg}(-\sqrt{x})$

Построить график функции:

а) $y = \arccos(2x) + \arccos(-2x)$;

$y = \arccos 2x + \pi — \arccos 2x = \pi;$
Область определения:
$-1 \leq 2x \leq 1;$
$-0.5 \leq x \leq 0.5;$
График функции:

б) $y = \arccos \frac{1}{x} + \arccos \left( -\frac{1}{x} \right)$;

$y = \arccos \frac{1}{x} + \pi — \arccos \frac{1}{x} = \pi;$
Область определения:
$-1 \leq \frac{1}{x} \leq 1;$
$x \leq -1, \ x \geq 1;$
График функции:

в) $y = \operatorname{arcctg} x + \operatorname{arcctg}(-x)$;

$y = \operatorname{arcctg} x + \pi — \operatorname{arcctg} x = \pi;$
Область определения:
$x \in \mathbb{R};$
График функции:

г) $y = \operatorname{arcctg} \sqrt{x} + \operatorname{arcctg}(-\sqrt{x})$;

$y = \operatorname{arcctg} \sqrt{x} + \pi — \operatorname{arcctg} \sqrt{x} = \pi;$
Область определения:
$\sqrt{x} \in \mathbb{R};$
$x \geq 0;$
График функции:

а) $y = \arccos(2x) + \arccos(-2x)$

Шаг 1. Упростим выражение для функции.
Рассмотрим выражение:

$$y = \arccos(2x) + \arccos(-2x)$$

Используем свойство функции арккосинуса:

$$\arccos(-z) = \pi — \arccos(z)$$

Таким образом, у нас получается:

$$y = \arccos(2x) + \pi — \arccos(2x)$$

Теперь видно, что два выражения $\arccos(2x)$ и $-\arccos(2x)$ взаимно уничтожаются, и остается только:

$$y = \pi$$

Шаг 2. Область определения.
Аргумент функции $\arccos$ должен находиться в интервале $[-1, 1]$, следовательно:

$$-1 \leq 2x \leq 1$$

Делим это неравенство на 2:

$$-0.5 \leq x \leq 0.5$$

Таким образом, область определения функции: $-0.5 \leq x \leq 0.5$.

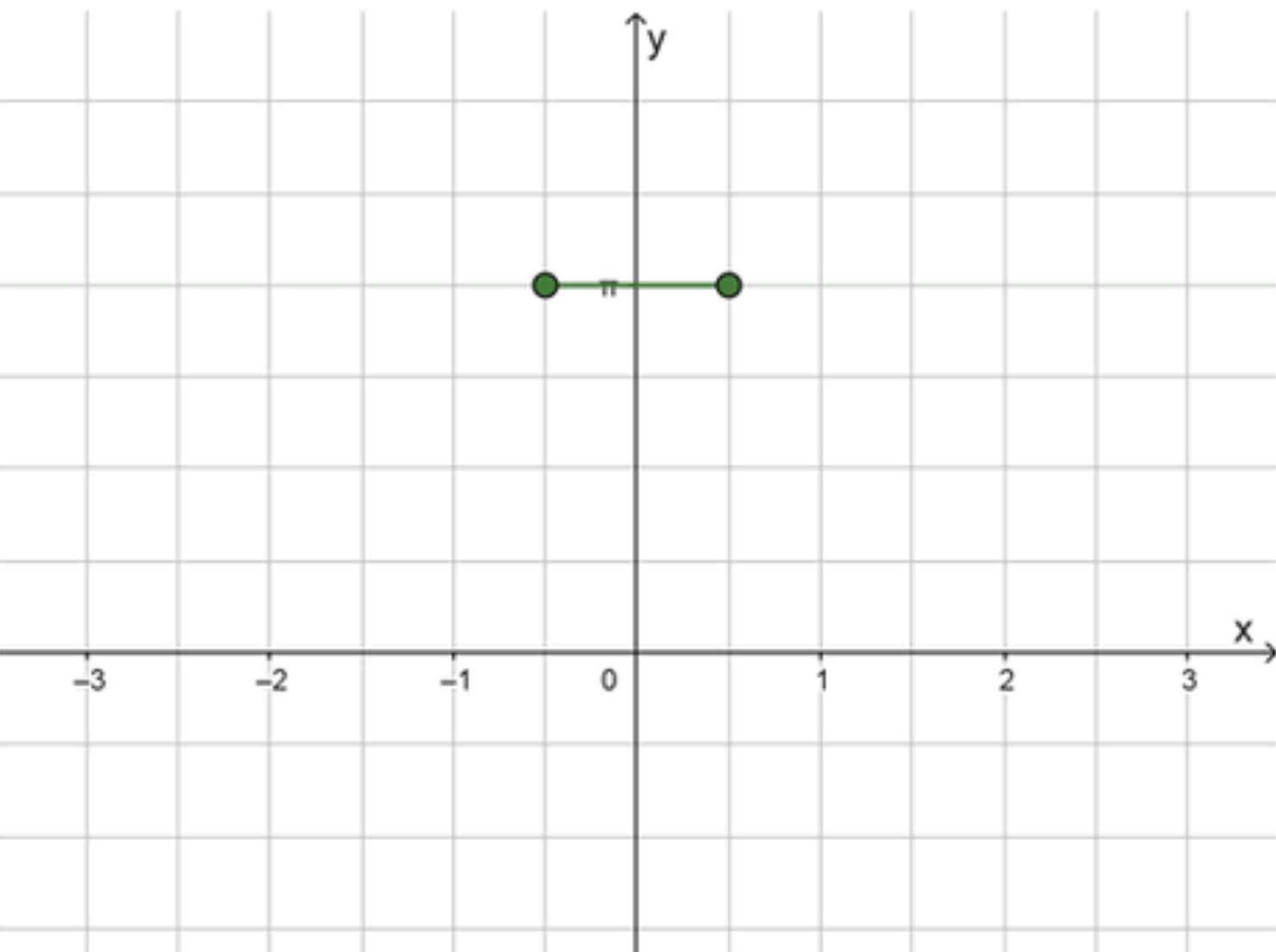
Шаг 3. График функции.
Функция $y = \pi$ является горизонтальной прямой, которая принимает значение $\pi$ на всем интервале области определения. График будет горизонтальной прямой от $x = -0.5$ до $x = 0.5$.

б) $y = \arccos \frac{1}{x} + \arccos \left( -\frac{1}{x} \right)$

Шаг 1. Упростим выражение для функции.
Применим свойство арккосинуса:

$$\arccos(-z) = \pi — \arccos(z)$$

Таким образом:

$$y = \arccos\left( \frac{1}{x} \right) + \pi — \arccos\left( \frac{1}{x} \right)$$

Как и в предыдущем примере, два выражения $\arccos\left( \frac{1}{x} \right)$ и $-\arccos\left( \frac{1}{x} \right)$ взаимно уничтожаются, и остается:

$$y = \pi$$

Шаг 2. Область определения.
Для того чтобы функции $\arccos\left( \frac{1}{x} \right)$ и $\arccos\left( -\frac{1}{x} \right)$ были определены, их аргументы должны быть в пределах $[-1, 1]$. То есть:

$$-1 \leq \frac{1}{x} \leq 1$$

Это условие выполняется, когда:

$$x \leq -1 \quad \text{или} \quad x \geq 1$$

Таким образом, область определения функции: $x \leq -1$ или $x \geq 1$.

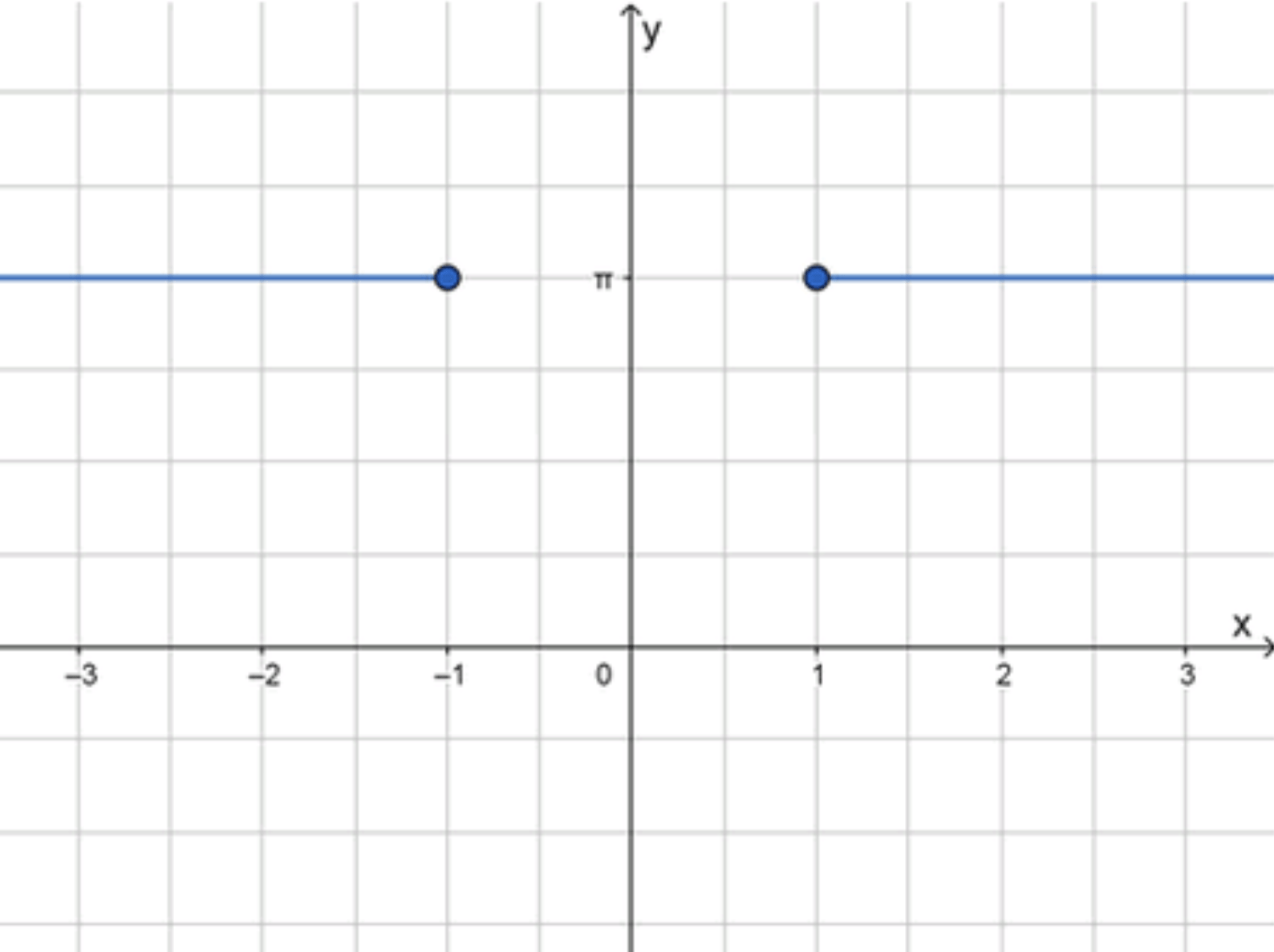
Шаг 3. График функции.
Функция $y = \pi$ является горизонтальной прямой, которая принимает значение $\pi$ на интервалах $(-\infty, -1]$ и $[1, \infty)$. График будет двумя горизонтальными прямыми, расположенными на уровне $y = \pi$, с разрывом между ними на интервале $(-1, 1)$.

в) $y = \operatorname{arcctg} x + \operatorname{arcctg}(-x)$

Шаг 1. Упростим выражение для функции.
Используем свойство функции арккотангенса:

$$\operatorname{arcctg}(-z) = \pi — \operatorname{arcctg}(z)$$

Таким образом:

$$y = \operatorname{arcctg}(x) + \pi — \operatorname{arcctg}(x)$$

Складываем два выражения $\operatorname{arcctg}(x)$ и $-\operatorname{arcctg}(x)$, и получается:

$$y = \pi$$

Шаг 2. Область определения.
Функция $\operatorname{arcctg}(x)$ определена для всех $x \in \mathbb{R}$, так как $\operatorname{arcctg}(x)$ существует для любого действительного числа. Следовательно, область определения функции: $x \in \mathbb{R}$.

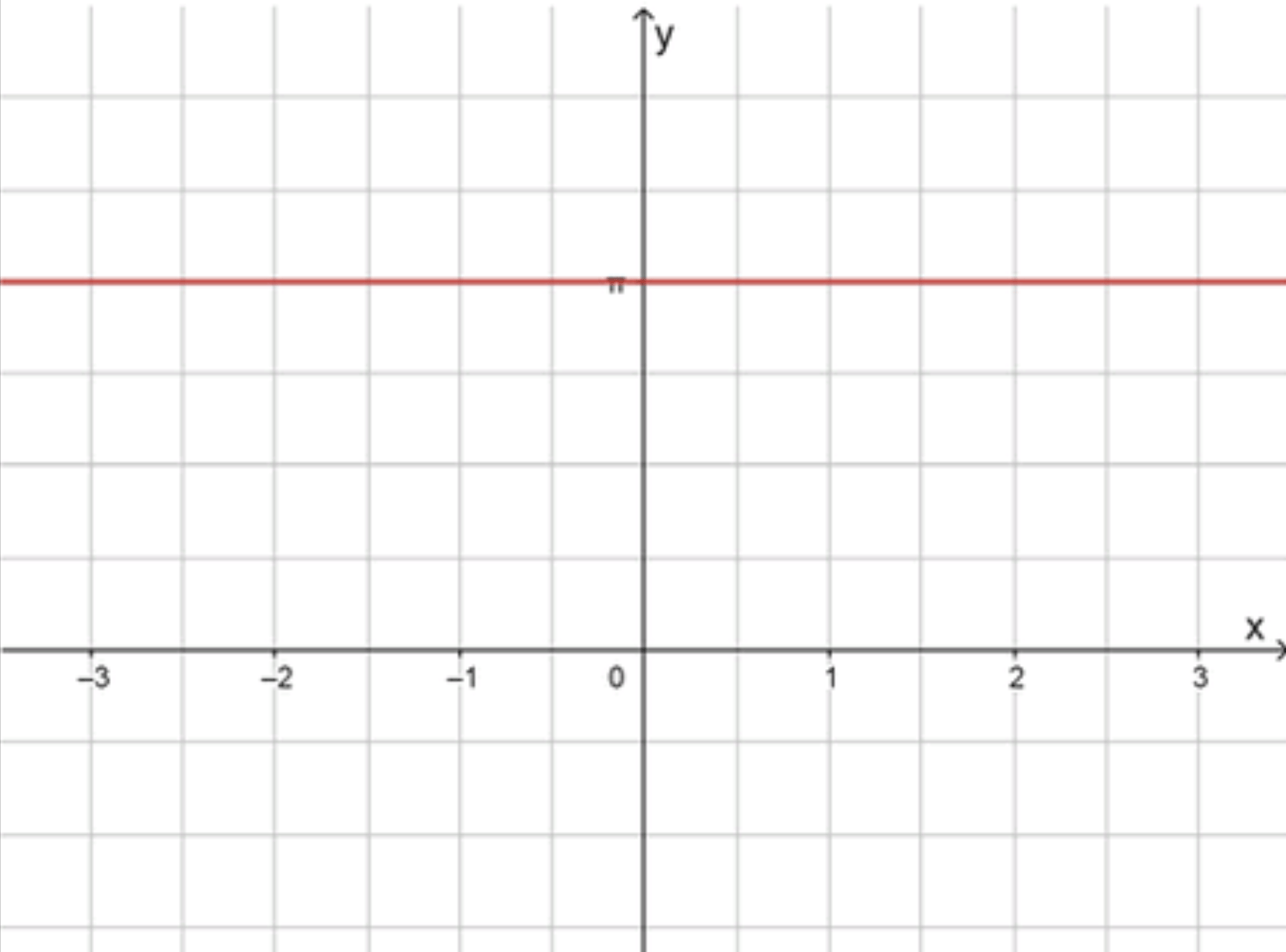
Шаг 3. График функции.
Функция $y = \pi$ является горизонтальной прямой, которая принимает значение $\pi$ на всем интервале $(-\infty, \infty)$.

г) $y = \operatorname{arcctg} \sqrt{x} + \operatorname{arcctg}(-\sqrt{x})$

Шаг 1. Упростим выражение для функции.
Используем свойство функции арккотангенса:

$$\operatorname{arcctg}(-z) = \pi — \operatorname{arcctg}(z)$$

Таким образом:

$$y = \operatorname{arcctg}(\sqrt{x}) + \pi — \operatorname{arcctg}(\sqrt{x})$$

Складываем два выражения $\operatorname{arcctg}(\sqrt{x})$ и $-\operatorname{arcctg}(\sqrt{x})$, и получается:

$$y = \pi$$

Шаг 2. Область определения.
Так как аргумент $\sqrt{x}$ должен быть действительным числом, необходимо, чтобы $x \geq 0$. Следовательно, область определения функции: $x \geq 0$.

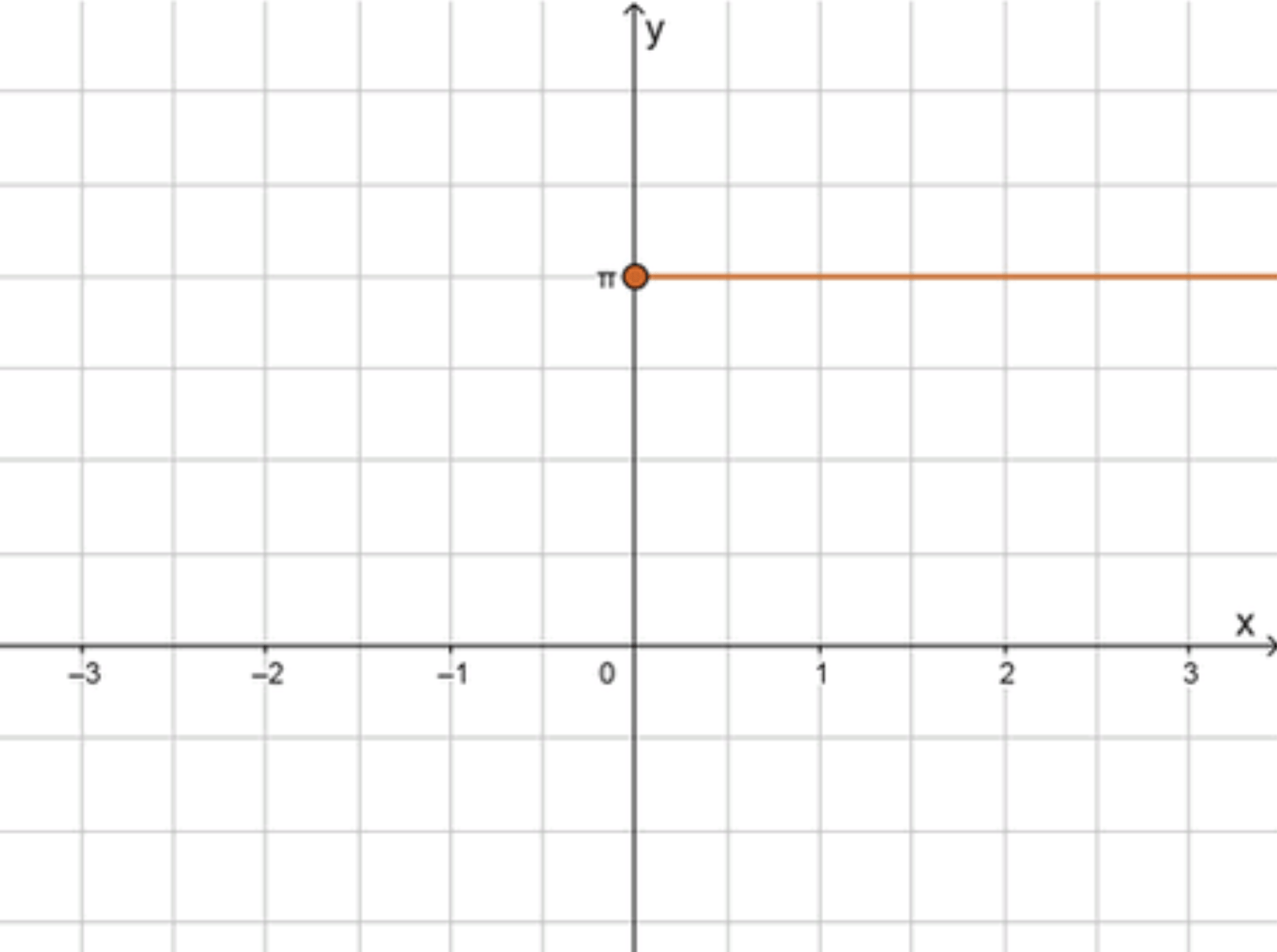
Шаг 3. График функции.
Функция $y = \pi$ является горизонтальной прямой, которая принимает значение $\pi$ на интервале $x \geq 0$. График будет горизонтальной прямой от $x = 0$ и вправо.