ГДЗ 10-11 Класс Номер 17.16 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y=\sin (\arcsin x)$

б) $y = \arctg x + \arctg(-x)$

в) $y=\mathrm{tg}(\mathrm{arctg}x)$

г) $y = \arcsin x + \arcsin(-x)$

Построить график функции:

а) $y = \sin(\arcsin x) = x$;

Область определения:
$-1 \leq x \leq 1$;

График функции:

б) $y = \arctg x + \arctg(-x)$;
$y = \arctg x — \arctg x = 0$;

Область определения:
$x \in \mathbb{R}$;

График функции:

в) $y = \operatorname{tg}(\arctg x) = x$;

Область определения:
$x \in \mathbb{R}$;

График функции:

г) $y = \arcsin x + \arcsin(-x)$;
$y = \arcsin x — \arcsin x = 0$;

Область определения:
$-1 \leq x \leq 1$;

График функции:

а) $y = \sin(\arcsin x) = x$

Шаг 1. Разбор выражения.

У нас есть выражение:

$$y = \sin(\arcsin x)$$

Это выражение состоит из двух функций: арксинуса и синуса. Мы знаем, что арксинус $\arcsin x$ — это функция, которая возвращает значение угла $\theta$, для которого:

$$\sin \theta = x, \quad -1 \leq x \leq 1$$

Иначе говоря, $\arcsin x$ возвращает угол, который дает синус, равный $x$.

Шаг 2. Свойства и упрощение.

Функция $\sin$ и функция $\arcsin$ являются обратными. То есть, если $y = \arcsin x$, то:

$$\sin(\arcsin x) = x$$

Это свойство позволяет упростить выражение:

$$y = x$$

Таким образом, $y = \sin(\arcsin x)$ — это просто $y = x$, при условии, что $x$ лежит в области определения функции арксинуса, то есть:

$$-1 \leq x \leq 1$$

Шаг 3. Область определения.

Так как арксинус определен только для значений $x$, лежащих в интервале $[-1, 1]$, то и область определения функции $y = \sin(\arcsin x)$ будет:

$$-1 \leq x \leq 1$$

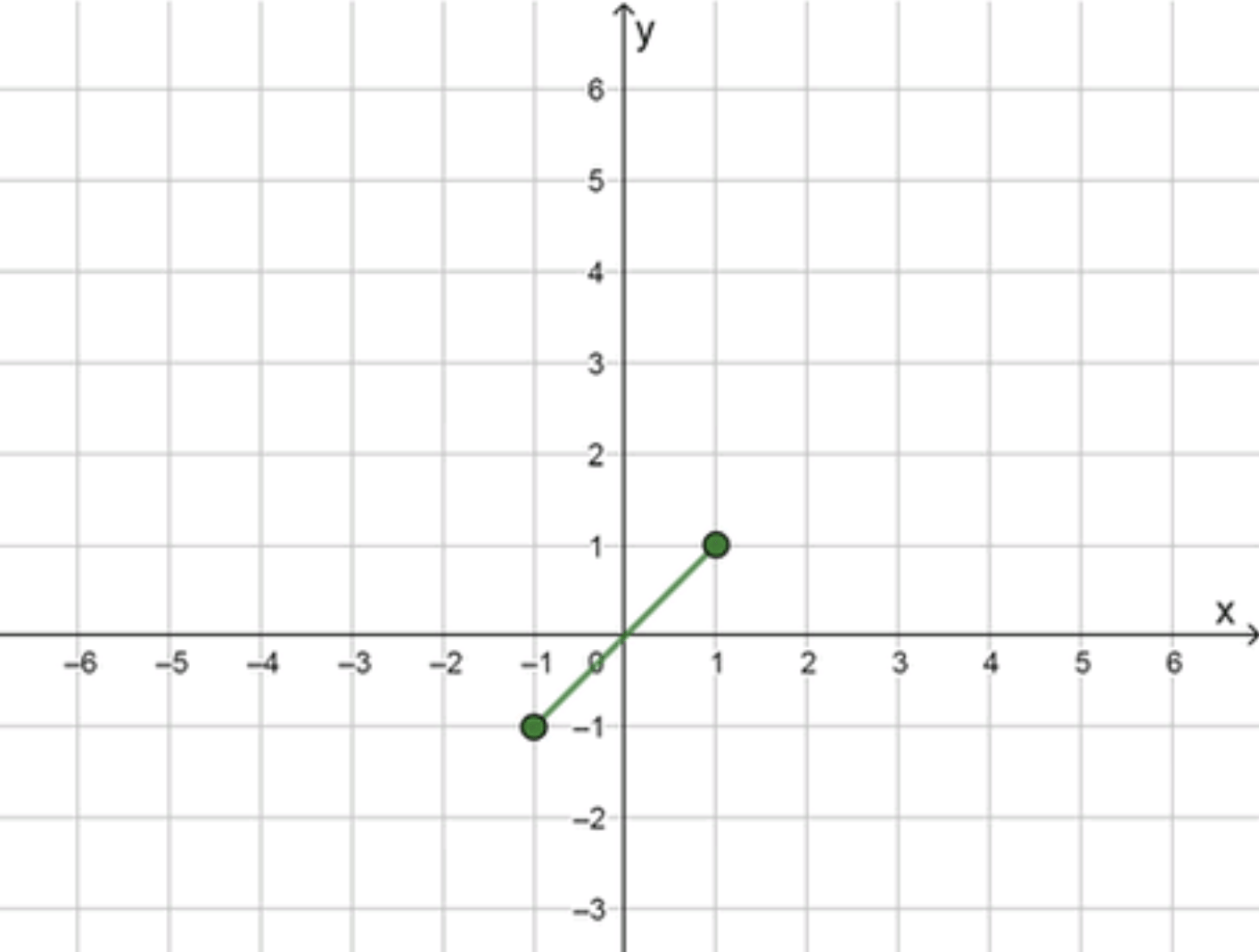
Шаг 4. График функции.

График функции $y = x$ — это прямая линия с угловым коэффициентом 1, которая проходит через начало координат. Однако область определения ограничена интервалом $-1 \leq x \leq 1$. Таким образом, график функции представляет собой отрезок прямой, проходящий от точки $(-1, -1)$ до точки $(1, 1)$.

б) $y = \arctg x + \arctg(-x)$

Шаг 1. Разбор выражения.

У нас есть выражение:

$$y = \arctg x + \arctg(-x)$$

Используем свойство арктангенса для отрицательного аргумента:

$$\arctg(-x) = -\arctg(x)$$

Подставляем это в исходное выражение:

$$y = \arctg x — \arctg x$$

Видим, что оба члена сокращаются, и получается:

$$y = 0$$

Шаг 2. Область определения.

Функция арктангенс $\arctg x$ определена для всех $x \in \mathbb{R}$, так как $\arctg x$ существует для всех действительных чисел. Следовательно, область определения функции $y = \arctg x + \arctg(-x)$ — это весь набор действительных чисел:

$$x \in \mathbb{R}$$

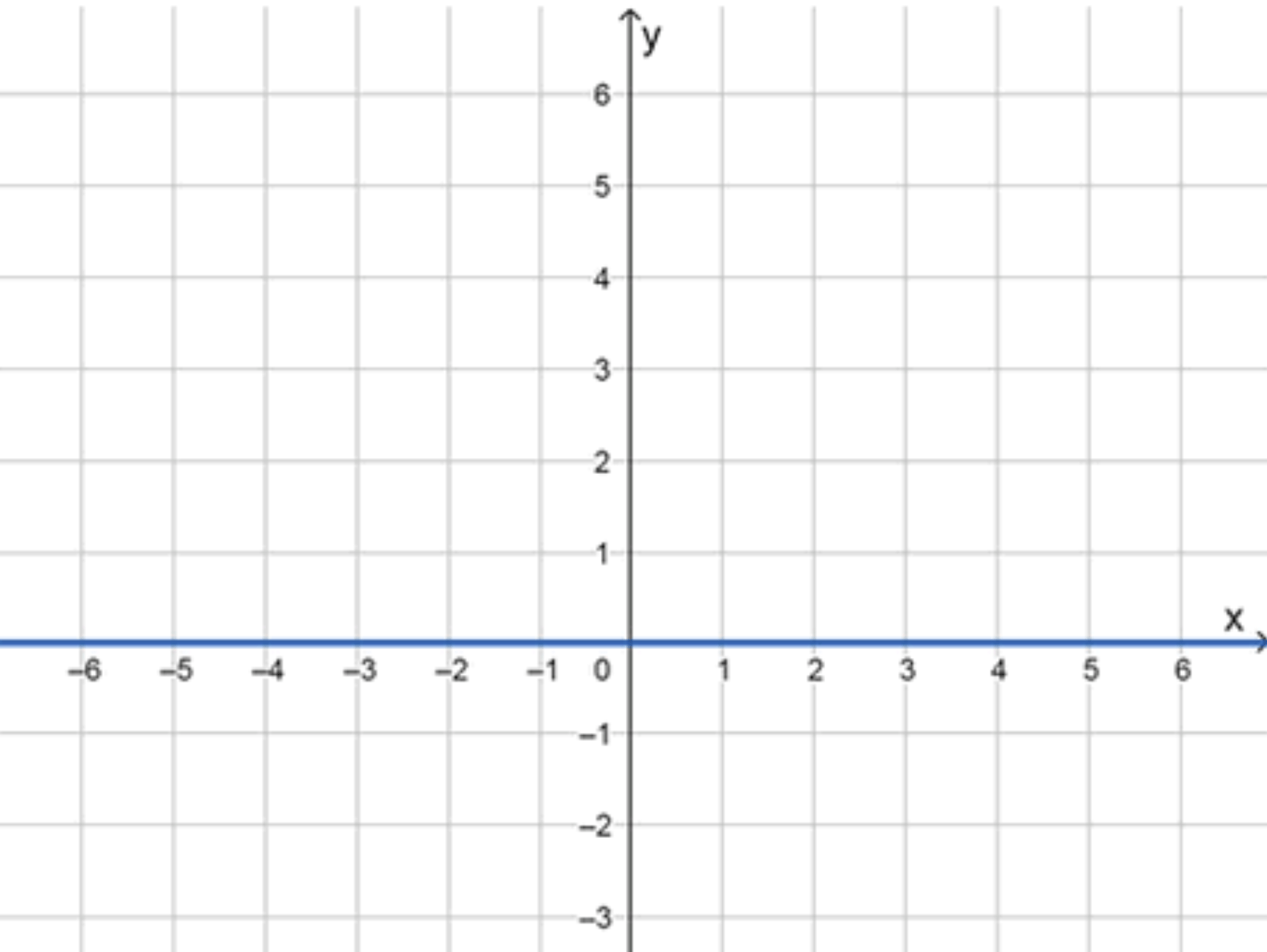
Шаг 3. График функции.

Так как $y = 0$ для всех значений $x \in \mathbb{R}$, график функции — это горизонтальная прямая, расположенная на оси $y = 0$ на всей числовой оси $x$.

в) $y = \operatorname{tg}(\arctg x) = x$

Шаг 1. Разбор выражения.

У нас есть выражение:

$$y = \operatorname{tg}(\arctg x)$$

Арктангенс $\arctg x$ — это функция, которая возвращает угол $t$, для которого $\operatorname{tg} t = x$. Если мы применим к этому углу функцию тангенса, то получим:

$$\operatorname{tg}(\arctg x) = x$$

Так как тангенс и арктангенс — это взаимно обратные функции, то результат будет просто $x$.

Шаг 2. Область определения.

Функция арктангенс $\arctg x$ определена для всех $x \in \mathbb{R}$, и функция тангенс также определена для всех действительных чисел. Следовательно, область определения функции $y = \operatorname{tg}(\arctg x)$ — это все $x \in \mathbb{R}$.

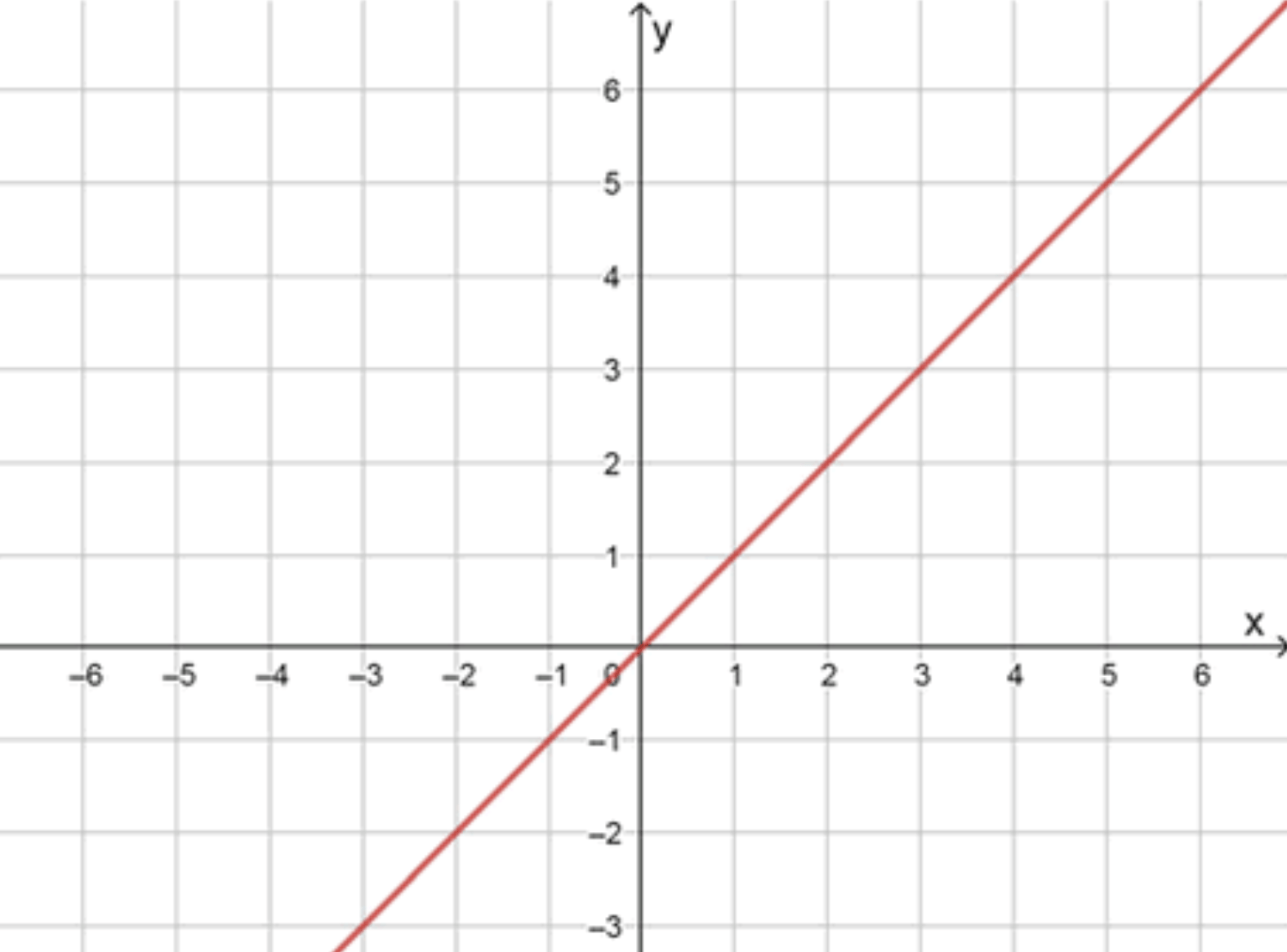
Шаг 3. График функции.

График функции $y = x$ — это прямая линия с угловым коэффициентом 1, которая проходит через начало координат и имеет вид:

$$y = x$$

На всей числовой оси $x$.

г) $y = \arcsin x + \arcsin(-x)$

Шаг 1. Разбор выражения.

У нас есть выражение:

$$y = \arcsin x + \arcsin(-x)$$

Используем свойство арксинуса для отрицательного аргумента:

$$\arcsin(-x) = -\arcsin(x)$$

Подставляем это в исходное выражение:

$$y = \arcsin x — \arcsin x$$

Как и в предыдущем случае, оба члена сокращаются, и получается:

$$y = 0$$

Шаг 2. Область определения.

Функция арксинус $\arcsin x$ определена для значений $x$ в интервале $[-1, 1]$. Следовательно, область определения функции $y = \arcsin x + \arcsin(-x)$ будет:

$$-1 \leq x \leq 1$$

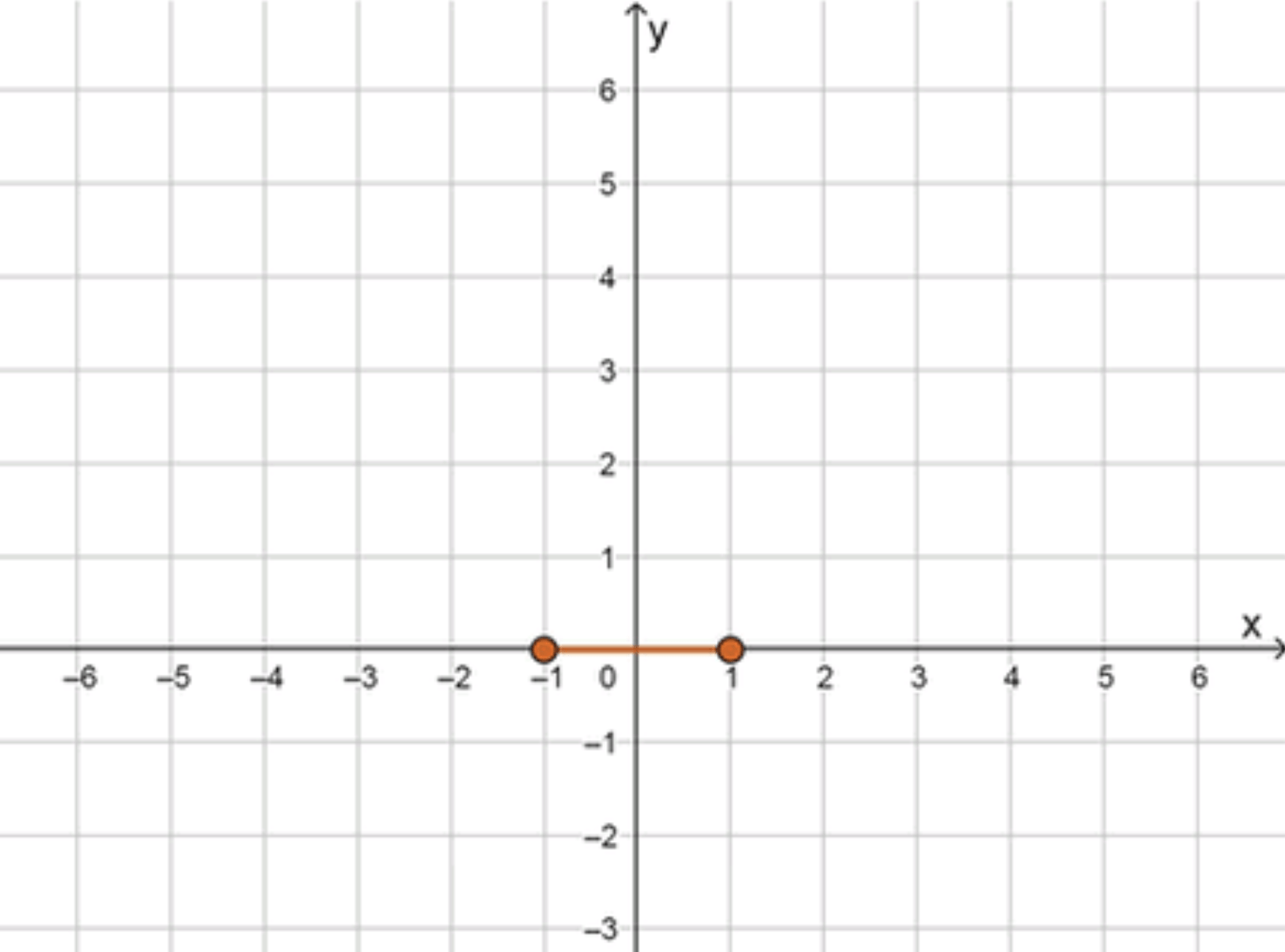
Шаг 3. График функции.

Так как $y = 0$ на интервале $-1 \leq x \leq 1$, график функции представляет собой горизонтальную прямую, расположенную на оси $y = 0$ в этом диапазоне значений $x$.