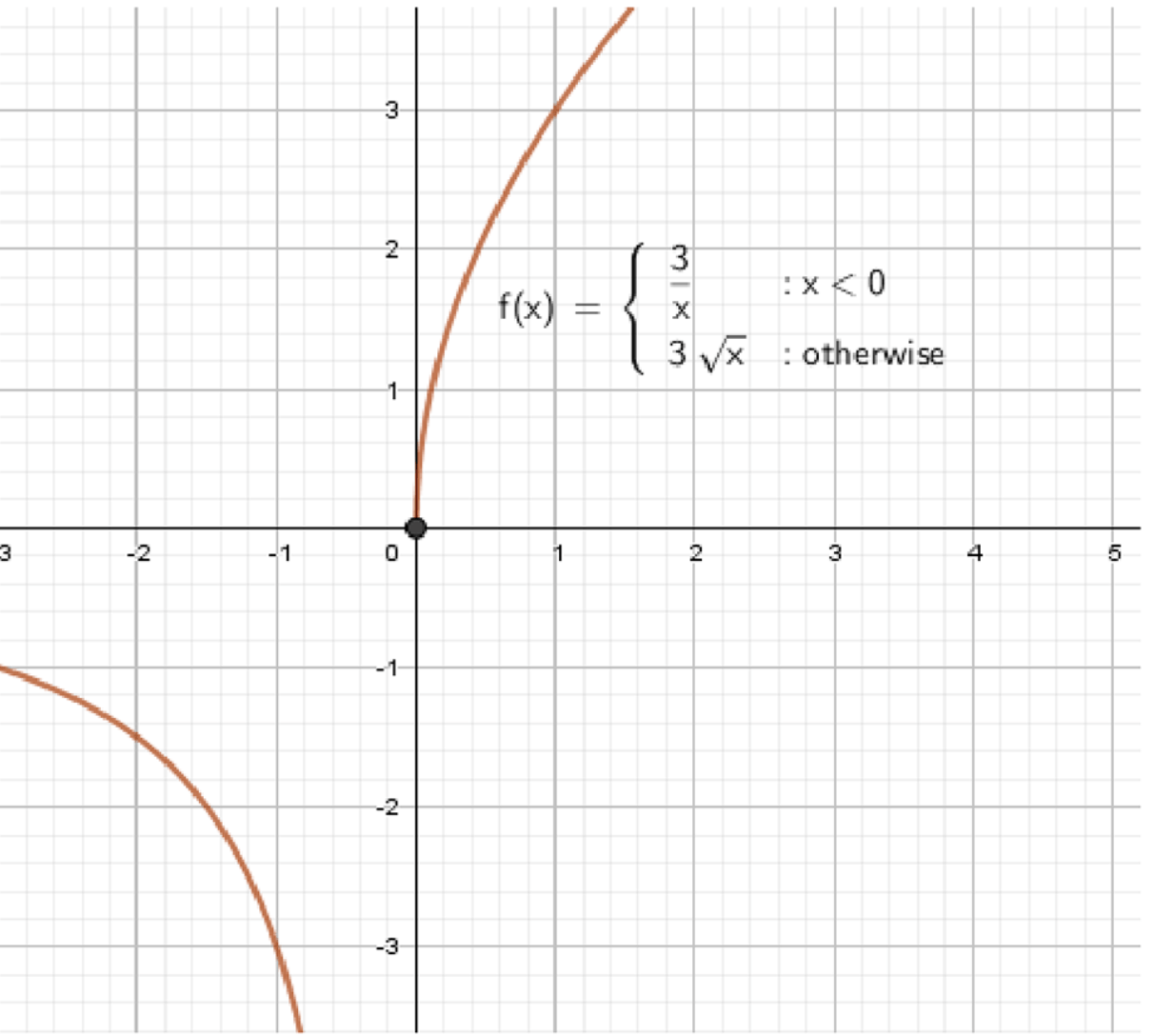ГДЗ 10-11 Класс Номер 2.12 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

$$y=\{\begin{array}{l}\frac{3}{x},\text{если }x<0\\ 3\sqrt{x},\text{если }x\ge 0\end{array}$$

Построить и прочитать график функции:

$$y=\{\begin{array}{l}\frac{3}{x},\text{если }x<0\\ 3\sqrt{x},\text{если }x\ge 0\end{array}$$

1) $y=\frac{3}{x}$ — уравнение гиперболы:

$x_0=0,y_0=0$;

2) $y=3\sqrt{x}$ — ветвь параболы:

$x_0=0,y_0=0$;

3) График функции:

4) Свойства функции:

• $D(y)=(-\mathrm{\infty };+\mathrm{\infty }),E(y)=(-\mathrm{\infty };+\mathrm{\infty })$;
• Возрастает на $[0;+\mathrm{\infty })$ и убывает на $(-\mathrm{\infty };0)$;
• Не ограничена ни снизу, ни сверху;
• $y_{\text{наим}}$ — не существует, $y_{\text{наиб}}$ — не существует;
• Функция непрерывна на $(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$;
• Имеет горизонтальную асимптоту $x=0$;
• Имеет вертикальную асимптоту $y=0$

Построить и прочитать график функции:

$$y=\{\begin{array}{l}\frac{3}{x},\text{если }x<0\\ 3\sqrt{x},\text{если }x\ge 0\end{array}$$

Шаг 1: Анализ каждой части функции

Функция состоит из двух частей, каждая из которых описывает разные поведения в зависимости от значения $x$.

Часть 1: $y=\frac{3}{x}$, когда $x<0$

Это уравнение гиперболы, которая имеет вертикальную асимптоту на оси $x=0$ и горизонтальную асимптоту на оси $y=0$.

• Когда $x$ отрицательное, то $y$ также будет отрицательным. При $x\to 0^{-}$ (когда $x$ стремится к нулю с левой стороны) $y$ стремится к $-\mathrm{\infty }$.
• При $x\to -\mathrm{\infty }$ (когда $x$ стремится к отрицательной бесконечности) $y$ стремится к $0^{-}$.

Исходя из этого, график функции будет выглядеть как гипербола, приближающаяся к оси $x$ и $y$.

Часть 2: $y=3\sqrt{x}$, когда $x\ge 0$

Это уравнение параболы. Функция $3\sqrt{x}$ определена только для $x\ge 0$, так как квадратный корень из отрицательного числа не существует в области действительных чисел.

• При $x=0$, $y=3\sqrt{0}=0$.
• Когда $x$ увеличивается, $y$ будет расти, но не так быстро, как $x$, так как это корень из $x$. Например, при $x=1$, $y=3\sqrt{1}=3$, при $x=4$, $y=3\sqrt{4}=6$, и так далее.

График функции $y=3\sqrt{x}$ представляет собой ветвь параболы, начинающуюся в точке $(0,0)$ и растущую вправо.

Шаг 2: Примерные значения для графика

Для построения графика полезно выбрать несколько значений $x$ и соответствующие им значения $y$ для каждой части функции.

Для $y=\frac{3}{x}$ (когда $x<0$):

Эти значения показывают, как функция ведет себя при приближении к нулю и в дальнейшем, когда $x$ становится всё более отрицательным.

Для $y=3\sqrt{x}$ (когда $x\ge 0$):

Эти значения помогают визуализировать поведение функции при положительных значениях $x$.

Шаг 3: Построение графика

• Для $x<0$: график будет гиперболой, которая убывает слева, подходя к оси $x$ и стремится к вертикальной асимптоте $x=0$, а также к горизонтальной асимптоте $y=0$.
• Для $x\ge 0$: график будет ветвью параболы, начиная с точки $(0,0)$, которая будет возрастать по мере увеличения $x$.

Таким образом, график будет выглядеть следующим образом:

Шаг 4: Свойства функции

Область определения (Домен функции):

• $x<0$ для первой части функции $y=\frac{3}{x}$, и $x\ge 0$ для второй части $y=3\sqrt{x}$.
• Таким образом, область определения всей функции:$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Область значений (Множество значений функции):

• Для части $y=\frac{3}{x}$ значения $y$ могут быть любыми отрицательными числами и стремиться к $0$ с минусом при $x\to -\mathrm{\infty }$.
• Для части $y=3\sqrt{x}$ значения $y$ всегда положительные или ноль.
• Таким образом, область значений функции:$$E(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

Монотонность:

• Функция возрастает на интервале $[0;+\mathrm{\infty })$, потому что для $x\ge 0$ функция $y=3\sqrt{x}$ растет.
• Функция убывает на интервале $(-\mathrm{\infty };0)$, потому что для $x<0$ функция $y=\frac{3}{x}$ убывает.

Ограниченность:

• Функция не ограничена ни снизу, ни сверху. В области $x<0$ функция может стремиться к $-\mathrm{\infty }$, а для $x\ge 0$ она не ограничена сверху.

Наличие экстремумов:

• Наибольшего значения $y$ не существует, так как для $x\to \mathrm{\infty }$, функция $y=3\sqrt{x}$ будет возрастать бесконечно.
• Наименьшего значения $y$ также не существует, так как для $x\to -\mathrm{\infty }$, функция $y=\frac{3}{x}$ стремится к $-\mathrm{\infty }$.

Непрерывность:

• Функция непрерывна на интервалах $(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$, так как каждая из частей функции определена и непрерывна на этих интервалах.

Ассимптоты:

• Функция имеет горизонтальную асимптоту $y=0$ для $x\to -\mathrm{\infty }$, так как $\frac{3}{x}\to 0$.
• Функция имеет вертикальную асимптоту $x=0$, так как $y=\frac{3}{x}$ стремится к бесконечности при $x\to 0^{-}$ и к минус бесконечности при $x\to 0^{+}$.