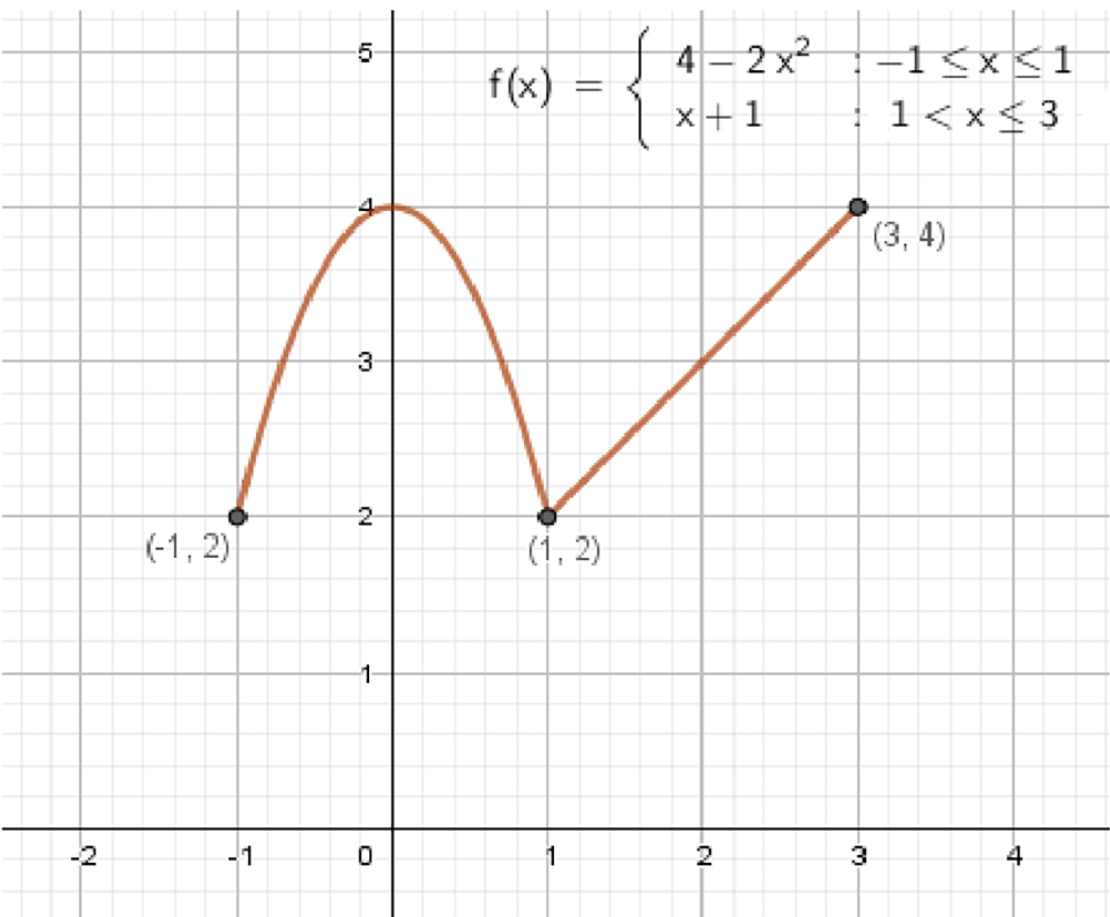ГДЗ 10-11 Класс Номер 2.13 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

$$y=\{\begin{array}{ll}4-2x^2,& \text{если }-1\le x\le 1\\ x+1,& \text{если }1<x\le 3\end{array}$$

Построить и прочитать график функции:

$$y = \begin{cases} 4 — 2x^2, & \text{если } -1 \leq x \leq 1; \\ x + 1, & \text{если } 1 < x \leq 3; \end{cases}$$

1) $y = 4 — 2x^2$ — уравнение параболы:

$x_0 = 0$, $y_0 = 4$;

2) $y = x + 1$ — уравнение прямой:

3) График функции:

4) Свойства функции:

• $D(y) = [-1; 3]$, $E(y) = [2; 4]$;
• Возрастает на $[-1; 0] \cup [1; 3]$ и убывает на $[0; 1]$;
• Ограничена снизу, ограничена сверху;
• $y_{\text{наиб}} = y(0) = 4$, $y_{\text{наим}} = y(1) = 2$;
• Функция непрерывна на $[-1; 3]$

Построить и прочитать график функции:

$$y = \begin{cases} 4 — 2x^2, & \text{если } -1 \leq x \leq 1; \\ x + 1, & \text{если } 1 < x \leq 3; \end{cases}$$

1. Анализ первой части функции: $y = 4 — 2x^2$ при $-1 \leq x \leq 1$

Это уравнение параболы. Чтобы подробно рассмотреть график этой функции, разберём её основные характеристики:

Коэффициенты:

• $a = -2$, это коэффициент перед $x^2$, который указывает на направление ветвей параболы (при $a < 0$ парабола открывается вниз).
• $b = 0$, коэффициент перед $x$.
• $c = 4$, свободный член.

Вершина параболы:
Вершина параболы, заданной уравнением вида $y = ax^2 + bx + c$, находится в точке $x_0 = -\frac{b}{2a}$. Подставим сюда наши коэффициенты:

$$x_0 = -\frac{0}{2(-2)} = 0.$$

Таким образом, вершина параболы находится в точке $x = 0$.

Теперь найдём значение $y_0$, то есть значение функции в вершине. Подставляем $x = 0$ в уравнение:

$$y_0 = 4 — 2(0)^2 = 4.$$

Следовательно, вершина параболы — это точка $(0, 4)$.

Пределы функции на отрезке $[-1; 1]$:
Подставим в уравнение значение $x = -1$:

$$y(-1) = 4 — 2(-1)^2 = 4 — 2 = 2.$$

Подставим $x = 1$:

$$y(1) = 4 — 2(1)^2 = 4 — 2 = 2.$$

Итак, на интервале $[-1, 1]$ график параболы будет иметь значения от $y = 2$ до $y = 4$, причём вершина будет в точке $(0, 4)$.

Ключевые точки на отрезке $[-1, 1]$:

$x = -1$, $y = 2$;

$x = 0$, $y = 4$;

$x = 1$, $y = 2$.

2. Анализ второй части функции: $y = x + 1$ при $1 < x \leq 3$

Это линейная функция с угловым коэффициентом $k = 1$ и сдвигом $b = 1$.

График прямой:
Это прямая линия, которая имеет угол наклона 45 градусов (так как угловой коэффициент равен 1). Прямая будет возрастать, поскольку $k = 1$.

Граничные точки на отрезке $(1; 3]$:
Подставим $x = 1$:

$$y(1) = 1 + 1 = 2.$$

Подставим $x = 3$:

$$y(3) = 3 + 1 = 4.$$

Таким образом, на интервале $(1, 3]$ значения функции будут изменяться от $y = 2$ до $y = 4$.

3. Построение графика функции

Для построения графика функции из двух частей нам нужно соединить два графика: параболу и прямую. Рассмотрим это поэтапно.

Для части $y = 4 — 2x^2$ на интервале $-1 \leq x \leq 1$, мы знаем, что:

• $y = 2$ при $x = -1$ и $x = 1$;
• $y = 4$ при $x = 0$.

Это — парабола, которая симметрична относительно оси $y$, с вершиной в точке $(0, 4)$ и уходит вниз.

Для второй части $y = x + 1$ на интервале $1 < x \leq 3$, это прямая линия с угловым коэффициентом 1:

• $y = 2$ при $x = 1$;
• $y = 4$ при $x = 3$.

Прямая будет пересекать точку $(1, 2)$ и идти вверх до точки $(3, 4)$.

График функции будет состоять из параболы на интервале $[-1, 1]$ и прямой на интервале $(1, 3]$, соединённых в точке $(1, 2)$.

4. Свойства функции

Теперь рассмотрим свойства функции на интервале $[-1; 3]$:

Область определения и область значений:

• $D(f) = [-1; 3]$, так как функция определена на отрезке $[-1, 3]$.
• $E(f) = [2; 4]$, так как функция принимает значения от 2 до 4, включая эти значения (точки $y = 2$ и $y = 4$ достигаются на концах интервала).

Монотонность функции:

• Функция возрастает на интервалах $[-1; 0]$ и $[1; 3]$:
  • На интервале $[-1; 0]$, поскольку $y = 4 — 2x^2$ (парабола с вершиной в $x = 0$, которая убывает для $x > 0$ и возрастает для $x < 0$).
  • На интервале $[1; 3]$, прямая $y = x + 1$ всегда возрастает.
• Функция убывает на интервале $[0; 1]$, так как парабола убывает в этом диапазоне.

Ограниченность:

• Функция ограничена сверху значением $y = 4$ при $x = 0$, и снизу значением $y = 2$ при $x = -1$ и $x = 1$.

Экстремумы:

• Максимум: Функция достигает максимума $y_{\text{max}} = 4$ в точке $x = 0$.
• Минимум: Функция достигает минимума $y_{\text{min}} = 2$ в точках $x = -1$ и $x = 1$.

Непрерывность:
Функция непрерывна на всём интервале $[-1; 3]$. Графики параболы и прямой соединены плавно в точке $(1, 2)$, где значения функции совпадают.

5. Выводы

Функция состоит из двух частей: параболы на интервале $[-1, 1]$ и прямой на интервале $(1, 3]$. Она непрерывна на всём заданном интервале, ограничена снизу и сверху, имеет максимум в точке $(0, 4)$ и минимум в точках $(-1, 2)$ и $(1, 2)$.