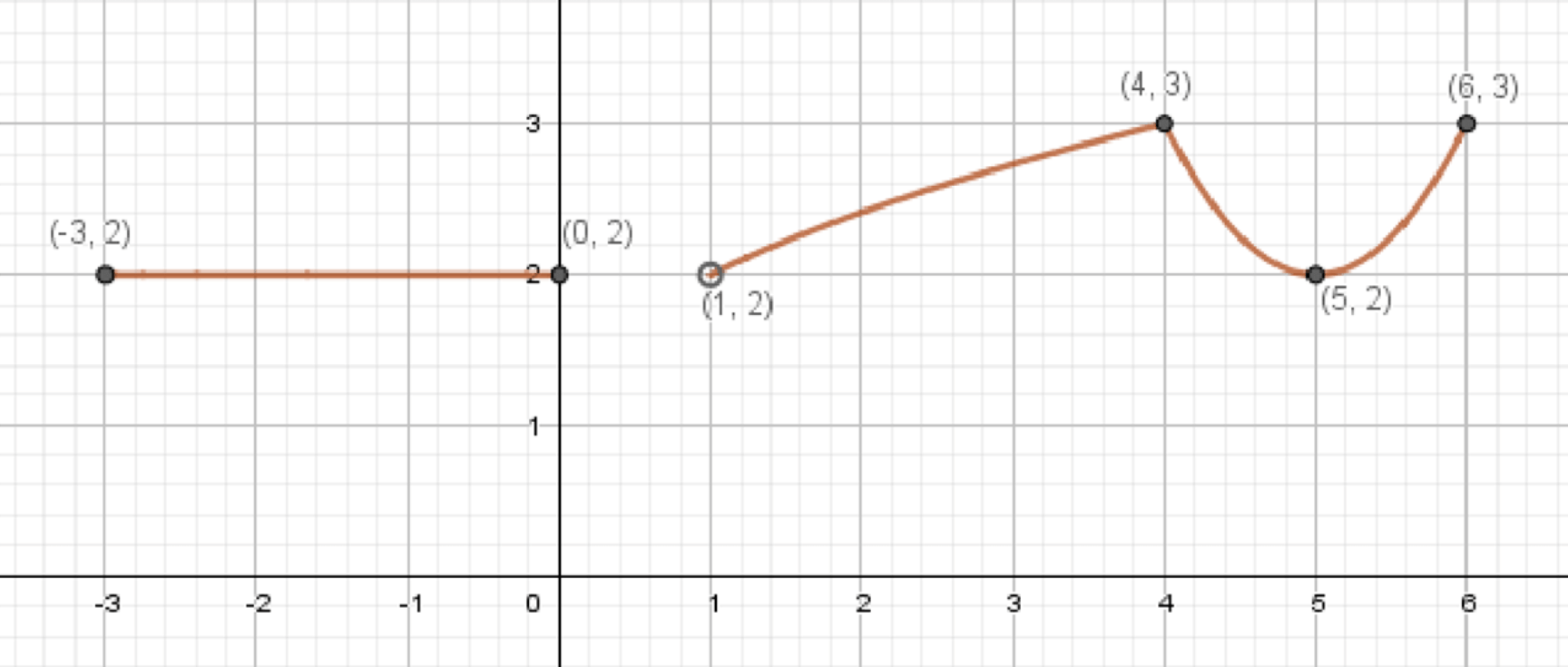ГДЗ 10-11 Класс Номер 2.14 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

$$y=\{\begin{array}{ll}2,& \text{если }-3\le x\le 1\\ \sqrt{x}+1,& \text{если }1<x\le 4\\ (x-5{)}^2+2,& \text{если }4<x\le 6\end{array}$$

Построить и прочитать график функции:

$$y = \begin{cases} 2, & \text{если } -3 \leq x \leq 1 \\ \sqrt{x} + 1, & \text{если } 1 < x \leq 4 \\ (x-5)^2 + 2, & \text{если } 4 < x \leq 6 \end{cases}$$

1) $y = \sqrt{x} + 1$ — ветвь параболы:

$x_0 = 0, \; y_0 = 1$;

2) $y = (x-5)^2 + 2$ — уравнение параболы:

$x_0 = 5, \; y_0 = 2$;

3) График функции:

4) Свойства функции:

• $D(y) = [-3; 6]$, $E(y) = [2; 3]$;
• Возрастает на $[1; 4] \cup [5; 6]$ и убывает на $[4; 5]$;
• Функция постоянна на $[-3; 1]$;
• Ограничена снизу, ограничена сверху;
• $y_{\text{наиб}} = y(4) = 3$, $y_{\text{наим}} = y(5) = 2$;
• Функция непрерывна на $[-3; 6]$.

Построить и прочитать график функции:

$$y = \begin{cases} 2, & \text{если } -3 \leq x \leq 1 \\ \sqrt{x} + 1, & \text{если } 1 < x \leq 4 \\ (x-5)^2 + 2, & \text{если } 4 < x \leq 6 \end{cases}$$

1. Анализ первой части функции: $y = 2$ при $-3 \leq x \leq 1$

Это постоянная функция на интервале $[-3; 1]$, которая всегда равна 2. График этой части будет горизонтальной прямой, проходящей через $y = 2$ на отрезке $x \in [-3; 1]$.

Граничные точки:

• При $x = -3$, $y = 2$.
• При $x = 1$, $y = 2$.

Вывод: На интервале $[-3; 1]$ функция принимает постоянное значение $y = 2$.

2. Анализ второй части функции: $y = \sqrt{x} + 1$ при $1 < x \leq 4$

Это уравнение функции, которая представляет собой ветвь параболы, смещённую вверх на единицу. Функция $\sqrt{x}$ — это корень квадратный из $x$, который определён только для $x \geq 0$.

Функция $\sqrt{x}$ возрастает от 0 при $x = 0$ и растёт с уменьшением скорости на более высоких значениях $x$.

Смещение на 1 вверх: Функция $\sqrt{x} + 1$ будет начинаться от $y = 2$ при $x = 1$, так как $\sqrt{1} + 1 = 2$.

Граничные точки:

• При $x = 1$, $y = 2$ (начало интервала).
• При $x = 4$, $y = \sqrt{4} + 1 = 2 + 1 = 3$.

Вывод: На интервале $(1, 4]$ функция возрастает, начиная с $y = 2$ при $x = 1$ и достигает значения $y = 3$ при $x = 4$.

3. Анализ третьей части функции: $y = (x — 5)^2 + 2$ при $4 < x \leq 6$

Это уравнение параболы, сдвинутой вправо на 5 единиц и вверх на 2 единицы. Основной функцией здесь является квадратичная функция $(x — 5)^2$, которая имеет вершину в точке $x = 5$, где значение функции минимально.

Функция $(x — 5)^2$ — это парабола, которая имеет минимум в точке $x = 5$.

Смещение на 2 единицы вверх: Парабола будет начинаться в точке $(5, 2)$, так как $(5 — 5)^2 + 2 = 2$.

Граничные точки:

• При $x = 4$, $y = (4 — 5)^2 + 2 = 1 + 2 = 3$.
• При $x = 6$, $y = (6 — 5)^2 + 2 = 1 + 2 = 3$.

Вывод: На интервале $(4, 6]$ функция убывает на интервале $(4, 5]$ и возрастает на интервале $[5, 6]$. Минимальное значение функции на этом интервале достигается при $x = 5$ (точка вершины параболы), где $y = 2$.

4. Построение графика функции

Для построения графика функции из трёх частей, нужно будет соединить графики каждой части поочерёдно:

Первая часть: На интервале $[-3; 1]$ функция постоянна, и её график — горизонтальная прямая, проходящая через $y = 2$.

Вторая часть: На интервале $(1; 4]$ функция $y = \sqrt{x} + 1$ возрастает от $y = 2$ при $x = 1$ до $y = 3$ при $x = 4$. Это будет график ветви параболы, возрастающий.

Третья часть: На интервале $(4; 6]$ функция $y = (x — 5)^2 + 2$ сначала убывает, а затем возрастает. Она достигает минимального значения $y = 2$ в точке $x = 5$, а потом возвращается к значению $y = 3$ при $x = 6$.

5. Свойства функции

Теперь давайте подробно рассмотрим свойства функции на всём интервале $[-3; 6]$:

Область определения и область значений:

• Область определения $D(y) = [-3; 6]$, так как функция задана на отрезке $[-3; 6]$.
• Область значений $E(y) = [2; 3]$, так как функция принимает значения от 2 до 3. При $x = -3$, $x = 1$, и $x = 5$ функция принимает значение 2, а при $x = 4$ и $x = 6$ — значение 3.

Монотонность функции:

• Возрастает на интервалах $[1; 4]$ и $[5; 6]$:
  • На интервале $[1; 4]$ функция $y = \sqrt{x} + 1$ возрастает, так как её производная $\frac{1}{2\sqrt{x}}$ положительна для $x > 0$.
  • На интервале $[5; 6]$ функция $y = (x — 5)^2 + 2$ возрастает, так как её производная $2(x — 5)$ положительна для $x > 5$.
• Убывает на интервале $[4; 5]$ на отрезке $(4; 5]$, так как парабола убывает до вершины.

Постоянность функции:

• Постоянна на интервале $[-3; 1]$, так как функция принимает одно и то же значение $y = 2$ на всём этом отрезке.

Ограниченность функции:

• Функция ограничена сверху значением $y = 3$, которое достигается при $x = 4$ и $x = 6$.
• Функция ограничена снизу значением $y = 2$, которое достигается при $x = -3$, $x = 1$ и $x = 5$.

Экстремумы:

• Максимум: $y_{\text{max}} = 3$ при $x = 4$ и $x = 6$.
• Минимум: $y_{\text{min}} = 2$ при $x = -3$, $x = 1$ и $x = 5$.

Непрерывность:

• Функция непрерывна на всём интервале $[-3; 6]$, так как она соединена плавно в каждой точке перехода между частями. На $x = 1$, $x = 4$ и $x = 5$ значения функции совпадают, не возникает разрывов.

6. Выводы

Функция состоит из трёх частей: постоянной функции на интервале $[-3; 1]$, возрастающей функции на интервале $(1; 4]$, и параболы с минимумом на интервале $(4; 6]$. Функция непрерывна, ограничена сверху и снизу, и достигает максимума при $y = 3$ и минимума при $y = 2$.